Пример 1. Решить неравенство:
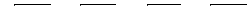(1)
Решение. Область определения неравенства (1): 2 £ х £ 3.
Прежде, чем возводить в квадрат обе части неравенства (1), необходимо убедиться в том, что обе его части неотрицательны.
Однако, оказывается, что это не так.
Действительно, так как 2 £ х £ 3, то 1 £ х – 1 £ 2 и 3 £ 6 – х £ 4. А это значит, что 
или 
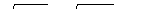. Но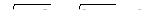 
. Таким образом, при всех значениях х из отрезка 2 £ х £ 3 неравенство (1) выполняется. Итак, 2 £ х £ 3 - решение неравенства.
Пример 2. Решим неравенство:
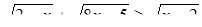
Решение. Найдем ОДЗ неравенства:
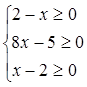
откуда получаем, что ОДЗ неравенства х = 2 – единственная точка. Подстановкой легко проверить, что х = 2 является решением исходного неравенства.
Ответ: х = 2.
12. Решение более сложных примеров.
Пример 1. Решить неравенство
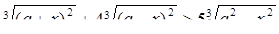
Решение. Используем метод интервалов. Решим соответствующее уравнение.
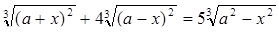
Решением уравнения являются значения переменной х = 0 и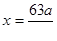 
при любом действительном значении параметра а.
Корни соответствующего уравнения разбивают числовую ось на промежутки знакопостоянтства, в каждом из которых неравенство или тождественно истинное, или тождественно ложное.
а) если a > 0, то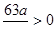 
и числовая ось разбивается на следующие промежутки знакопостоянства: x < 0,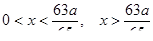 
Рассмотрим промежуток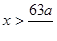 
. Возьмем значение х = а из этого промежутка и подставим в данное неравенство. Получим: 
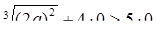- истинное числовое неравенство. Следовательно, промежуток 
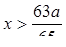принадлежит решению. Любое значение переменной х, взятое из промежутка знакопостоянства 
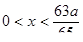, обращает данное неравенство в ложное числовое неравенство. Например, при 
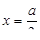имеем ложное числовое неравенство 
.
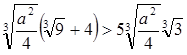Следовательно, промежуток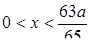 
не принадлежит решению.
Подставив, например, х = -а, взятое из промежутка знакопостоянства x < 0, в данное неравенство, получим истинное числовое неравенство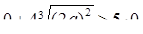 
. Значит, числовой промежуток x < 0 принадлежит решению. Итак, при a > 0 решением неравенства является объединение двух числовых промежутков x < 0 и 
.
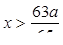б) если a < 0, то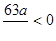 
и числовая ось разбивается на промежутки знакопостоянства 
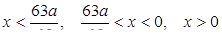. Как и в первом случае, устанавливаем, что данное неравенство тождественно истинное в промежутках 
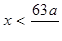и x > 0 и тождественно ложное в промежутке 
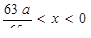. Следовательно, при a < 0 решением неравенства будет объединение двух числовых промежутков 
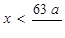и x > 0.
в) при а = 0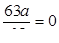 
. Получим два промежутка знакопостоянства: x < 0 и x > 0, каждый из которых, как легко установить принадлежит решению.
Ответ: 1) при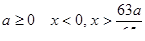 
2) при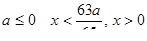 
.
Пример 2. Решить неравенство
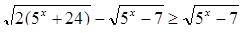
ОДЗ: 5х – 7 ≥ 0
log57 ≤ x < +∞
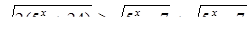
Возводим обе части в квадрат:
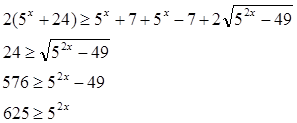
решением последнего неравенства является промежуток х ≤ 2. Учитывая ОДЗ получаем решение исходного неравенства log57 ≤ x ≤ 2.
Ответ: log57 ≤ x ≤ 2.
Дата: 2019-07-24, просмотров: 246.
