Потребность в действиях возведения в степень и извлечения корня была вызвана, как и другие четыре арифметические действия, практической жизнью. Так, наряду с задачей вычисления площади квадрата, сторона которого 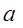 известна, с давних времен встречалась обратная задача: какую длину должна иметь сторона квадрата, чтобы его площадь равнялась
известна, с давних времен встречалась обратная задача: какую длину должна иметь сторона квадрата, чтобы его площадь равнялась 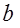 ?
?
Еще 4000 лет назад вавилонские ученые составляли наряду с таблицами умножения и таблицами обратных величин таблицы квадратов чисел и квадратных корней из чисел? При этом они умели находить приближенное значение квадратного корня из любого целого числа. Вавилонский метод извлечения квадратного корня можно иллюстрировать на следующем примере, изложенном в одной из найденных при раскопках клинописных табличек: Найти квадратный корень из 1700.
Для решения задачи данное число разлагается на сумму двух слагаемых:
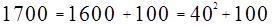 ,
,
первое из которых является полным квадратом. Затем указывается, что
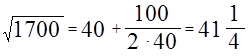
Правило, применявшееся вавилонянами, может быть выражено так: чтобы извлечь корень из числа 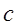 , разлагают его на сумму
, разлагают его на сумму 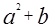 (
( 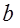 должно быть достаточно малым в сравнении с
должно быть достаточно малым в сравнении с 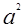 ) и вычисляют по приближенной формуле:
) и вычисляют по приближенной формуле:
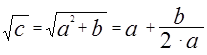
Вавилонский метод извлечения квадратного корня был заимствован греками. Так, например, у Герона Александрийского находим:
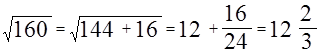
Для обозначения высших степеней употреблялись позже составные выражения "биквадрат" или "квадрато-квадрат" для четвертой степени, или "кубоквадрат" для пятой и т.д. Современные названия предложены голландским ученым С.Стевином (1548-1620), который обозначал степени в виде 2, 3 и т.д. Он же начал систематически употреблять дробные показатели степени для обозначения корней.
В настоящее время для извлечения корня употребляется два обозначения: знак радикала и дробные показатели. Предпочтительнее использовать обозначения со знаком радикала - обозначения с дробными показателями являются скорее данью традиции. Степени с отрицательными показателями ввел английский математик Д.Уоллис.
Неравенства встречаются в математике еще в глубокой ревности. Рассмотрим некоторые из них.
1. Среднее геометрическое двух положительных чисел 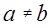 меньше их среднего арифметического (Евклид).
меньше их среднего арифметического (Евклид).
2. Архимед установил неравенства
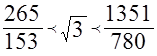
3. Если 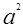 - наибольший квадрат, содержащийся в числе, а
- наибольший квадрат, содержащийся в числе, а 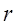 - остаток, то
- остаток, то
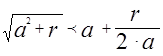 при
при 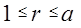
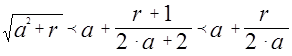 при
при 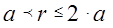
(Аль-Кальсади, Трактат "Раскрытие тайн науки Габар", XV век).
Дальнейшие обобщения натуральных, целых, рациональных и т.д. чисел привели к понятию алгебраической системы, в частности, к понятию кольца и поля. Так, иррациональные числа с алгебраической точки зрения являются элементами поля 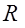 , они не содержатся в поле
, они не содержатся в поле 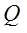 , и поле
, и поле 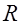 является расширением поля
является расширением поля 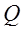 .
.
Дата: 2019-07-24, просмотров: 337.