Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

    Параметром называют такую переменную, значения которой постоянны в пределах рассматриваемой задачи .

    Значения параметров 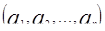, для которых функци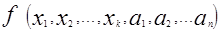и и 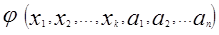определены, называются множеством допустимых значений параметров.

    Неравенство, содержащее параметры, только тогда считается решенным, когда указано множество всех его решений при произвольной допустимой системе значений параметров. Решение параметрических иррациональных неравенств рассмотрим на примерах. Чтобы проанализировать все допустимые значения параметров и найти соответствующие искомые значения переменной, целесообразно данное неравенство заменить эквивалентной совокупностью неравенств, как это будет показано ниже на примерах.

Пример 1. Решить и исследовать неравенство:

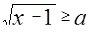(1)

Решение. Найдем ОДЗ неравенства (1) 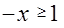. Неравенство (1) заменим эквивалентной совокупностью неравенств

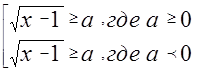
           Ясно, что второе неравенство будет истинно при любом 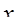из ОДЗ, т.к. 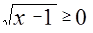, 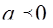. Первое неравенство совокупности имеет и правую и левую положительные части. Возведем в квадрат обе его части.

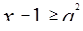
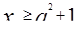
Все значения 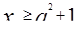будут принадлежать ОДЗ, так как 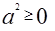, значит .

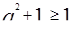Ответ: 1. 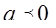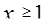; 2. .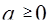

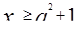Пример 2. Решить неравенство

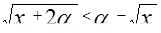
Решение. Легко видеть, что при 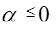данное неравенство не имеет решений, т.к. получаем положительную левую часть меньше отрицательно правой. что не имеет смысла. Рассмотрим неравенство при 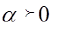. ОДЗ неравенства

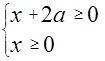
Неравенство имеет смысл лишь при 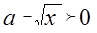. Получаем систему неравенств, эквивалентную исходному неравенству:

             

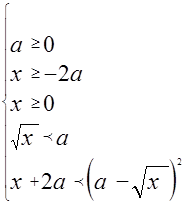
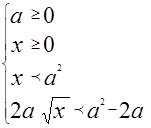
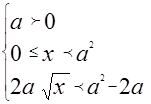
Решим последнее неравенство системы. Видим, что оно имеет смысл лишь при 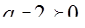. Возведем в квадрат обе части неравенства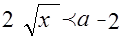

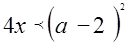при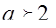

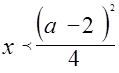
Сравним 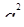и 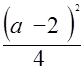, чтобы определить верхнюю границу значений .

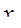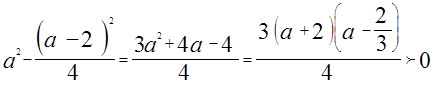
при 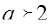значит > .

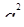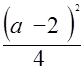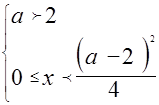
Ответ: если 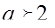, то

       если 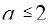. то .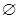

Пример 3. Решить неравенство

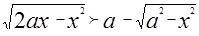
Решение. Данное неравенство перепишем так

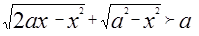(1)

 

 

Легко видеть, что при а = 0 неравенство решения не имеет. Рассмотрим значение параметра а > 0 и а < 0: левая и правая части неравенства положительные, поэтому при возведением неравенства в квадрат получим неравенства, эквивалентное данному в области его определения. При a < 0 данное неравенство тождественно истинное в области его определения (левая часть

неотрицательная, а правая отрицательная). Поэтому данное неравенство можно заменить следующей эквивалентной совокупностью систем неравенств:

 

 

 

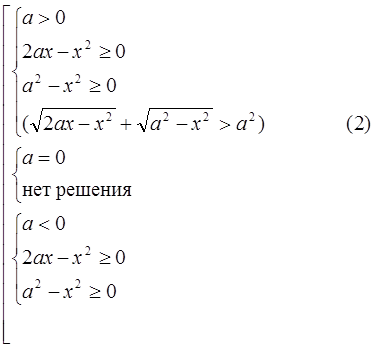
Рассмотрим неравенство (2). После выполнения преобразований получим:

 

 

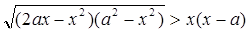
При a > 0 значения х = а и х = 0 не удовлетворяют неравенству, а при всех значениях 0 < x < a указанное неравенство тождественно истинное, поэтому первая система совокупности эквивалентна системе:

 

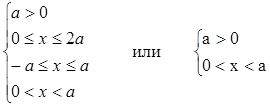
Итак, решение неравенства (1)

 

1) если а > 0 0 < x < a

2) если а = 0 нет решений

3) если a < 0 a £ x £ 0

 

Пример 4. Решить неравенство:

 

 

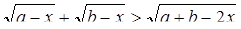
Решение. Возводим неравенство в квадрат. Так как левая и правая части неравенства неотрицательны, то эквивалентность не нарушается в области определения неравенства. Первый радикал имеет смысл при x £ а, второй при x £ b. При этих же значениях переменной имеет смысл и выражение, стоящее в правой части неравенства.

Итак,

 

       

 

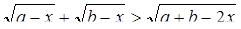
равносильно системе

 

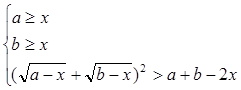
но

,

 

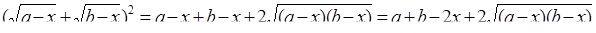значит последнее неравенство системы равносильно неравенству:

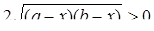
или

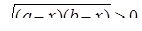
А система равносильна системе

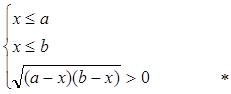
* выполняется, если оба множителя под корнем больше нуля или оба меньше нуля, значит наша система равносильна совокупности двух систем:

 

                                                       

 

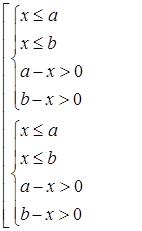
после выполнения преобразований получаем:

 

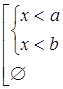
Видим, что в первой системе может быть два случая:

1) a ³ b,

2) b ³ a.

В первом случае решением системы будет x < b, а во втором x < a.

Ответ:   1) a ³ b x < b

      2) a £ b x < а

8. Решение иррациональных неравенств, способом введения новой переменной.

Иррациональные неравенства, как и иррациональные уравнения можно решать способом введения новой переменной. Рассмотрим использование этого метода на примерах.

 

Пример 1. Решить неравенство:

 

 

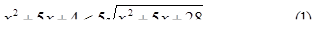
Решение. Положив 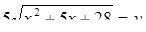, находим что х² + 5х + 4 = у² – 24, тогда неравенство (1) преобразуется к виду:

 

у² – 5y – 24 < 0

 

и далее решим уравнение:

 

у² – 5y – 24 = 0

D = 25 + 96 = 121

y₁ = -3, y₂ = 8

 

получаем (у – 8)(у + 3) < 0.

Решением этого неравенства является промежуток  -3 < y < 8.

Мы пришли к следующей системе неравенств:

 

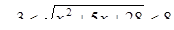
Так как 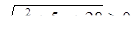 при всех допустимых значениях х, то тем более  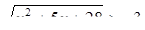  при всех х их ОДЗ неравенства (1), а поэтому достаточно решить неравенство:

 

 

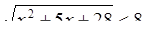
Это неравенство равносильно системе

 

 

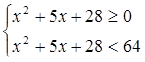
Так как неравенство х² + 5х + 38 ³ 0 выполняется при любых значениях х (D = 25 – 4 × 28 < 0 и а = 1 > 0), то последняя система равносильна неравенству:

 

х² + 5х + 38 < 0

 

или

 

(х + 9)(х – 4) < 0

 

откуда методом интервалов находим решение неравенства (1)

 

 

 

Ответ: х Î ]-9; 4[

Неравенство (1) – неравенство вида

 

.

 

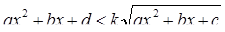Здесь применима подстановка 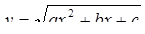и неравенство заменяется равносильным ему неравенством:

 

у² – ky + d – c < 0, которое легко разрешимо.

 

Рассмотрим неравенство вида:

 

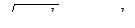, где можно применить подстановку .

 

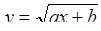Пример 2. Решить неравенство:

 

 

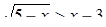
Решение. Найдем ОДЗ неравенства: х £ 5. Положим 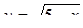, тогда у > x – 3, y ³ 0. Выразим х через у: у² = 5 – х Þ х = 5 – у².

Получаем систему:

 

 

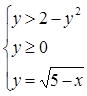
Откуда:

 

 

 

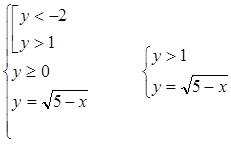
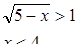
Значения x < 4 принадлежат ОДЗ.

Ответ: x < 4.

 

Пример 3. Решить неравенство

 

 

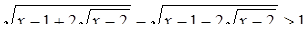
Решение. Найдем ОДЗ неравенства

 

 

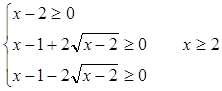
при х ³ 2 второе и третье неравенства системы истинны. ОДЗ х ³ 2.

Пусть 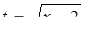, тогда исходное неравенство примет вид:

 

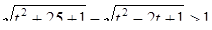                  (1)

 

Так как под радикалами в левой части неравенства (1) стоят полные квадраты, то оно может быть представлено в следующем эквивалентном виде:

|t + 1| - |t – 1| > 1

 

Разобьем решение на три промежутка:

 

1) t £ -1

-t – 1 + t – 1 > 1    Æ

2) –1 < t £ 1

t + 1 + t – 1 > 1

2t > 1

t > ½

3) t > 1

t + 1 – t + 1 > 1 2 > 1 – истинно

 

Решением неравенства на всех трех промежутках будет t > ½

Подставляем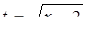

 

 

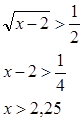
Эти значения принадлежат ОДЗ.

Ответ: x > 2,25.

 

Пример 4. Решить неравенство:

 

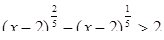
Решение. Положим 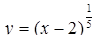, тогда  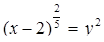 и мы получаем неравенство:

 

у² – у – 2 >0,

 

откуда находим y < -1, y>2.

Теперь задача свелась к решению двух неравенств:

 

 

Первое неравенство не имеет корней во множестве действительных чисел, поскольку под знаком возведения в дробную степень может содержаться только неотрицательное число, а любая степень неотрицательного числа неотрицательна.

 

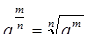                 (1)

 

Пусть a < 0. В школьном курсе рациональная степень числа а не определяется, и это не случайно. Пусть (1) верно, тогда:

 

 

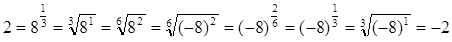
Противоречие.

Итак, получаем: левая положительная часть меньше отрицательной правой, что не имеет смысла.

Решим неравенство

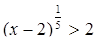
Возведем обе части неравенства в пятую степень, получим x – 2 > 32, откуда x > 34.

Ответ: x > 34.