КУРСОВОЙ ПРОЕКТ
на тему: «Механизмы компрессора»
Структурный анализ механизмов
Структурный анализ рычажного механизма
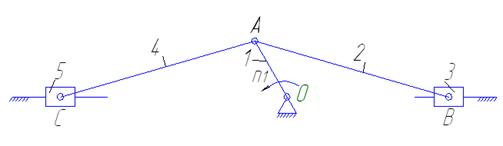
Рисунок 1.1. Подвижные звенья механизма
1-кривошип
2-шатун
3-ползун
4-шатун
5-ползун
Кинематические пары.
О (0-1),вр.,5 кл.
А (1-4),вр.,5 кл.
А'(1-2),вр.,5 кл.
В (2-3),вр.,5 кл.
В'(3-0),пост.,5 кл.
С (4-5),вр.,5 кл.
С'(5-0),пост.,5 кл.
Найдём число степеней свободы.
Запишем формулу Чебышева.
W=3∙n-2∙P5-P4 (1.1)
Где, W-число степеней свободы,
n-число подвижных звеньев,
P4 - число пар 4-го класса,
P5 - число пар 5-го класса.
W=3∙5-2∙7=1
Число степеней свободы рычажного механизма равно 1.
Разобьём механизм на группы Асура и рассмотрим каждую группу в отдельности.
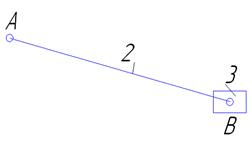Группа 2-3 (Рисунок 1.2)
A'(1-2)-внешняя
B'(3-0)-внешняя
B (2-3)-внутренняя
W=3∙2-2∙3=0
II кл. 2 вид Рисунок 1.2
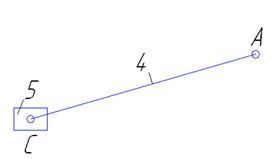Группа 4-5 (Рисунок 1.3)
А (1-4)-внешняя
С' (5-0)-внешняя
C (4-5)-внутренняя
W=3∙2-2∙3=0
II кл. 2 вид
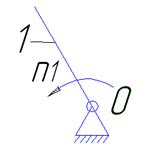
O (0-1)
W=3-2=1
Рисунок 1.4
Составим структурную формулу: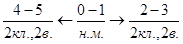 
Механизм является механизмом 2кл.,2в..
Структурный анализ зубчатого механизма
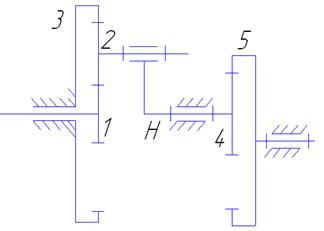
Рисунок 1.5. Подвижные звенья механизма
1 – центральное колесо
2 – сателлит
3 – зубчатое колесо
H – водило
4 – зубчатое колесо
5 – зубчатое колесо
Кинематические пары.
(1-0),вр.,5 кл.
(5-0),вр.,5 кл.
(2-H),вр.,5 кл.
(4-0),вр.,5 кл.
(1-2),вр.,4 кл.
(2-3),вр.,4 кл.
(4-5),вр.,4 кл.
Найдём число степеней свободы.
Исходя из формулы Чебышева имеем,
W=3∙4-2∙4-3=1
Число степеней свободы зубчатого механизма равно 1, следовательно, данный механизм является планетарным.
Структурный анализ кулачкового механизма
Рисунок 1.6. Подвижные звенья механизма
1-кулачок
2-ролик
3-коромысло
Кинематические пары.
О (1-0),вр.,5 кл.
А (3-0),вр.,5 кл.
В (2-3),вр.,5 кл.
С (1-2),пост.,4 кл.
Найдём число степеней свободы.
W=3∙n-2∙P5-P4
W=3∙3-2∙3-1=2
Число степеней свободы равно 2.
Так как W≠1, то присутствует лишнее звено - ролик.
Динамический анализ рычажного механизма
Определение скоростей
Для заданной схемы механизма строим 12 положений.
Определяем масштабный коэффициент построения механизма:
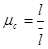(2.1)
где,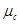 
- масштабный коэффициент,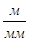 
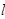- длина звена,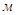 
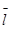- длина звена на чертеже,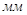 
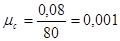
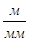
Запишем длинны звеньев механизма на чертеже
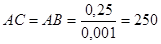
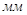
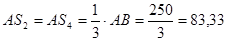
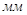
Приступаем к построению повёрнутых планов скоростей для каждого положения. Рассмотрим пример построения для положения №5:
У кривошипа определяем скорость точки А
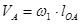(2.2)
где,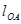 
- длина звена,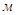
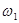- угловая скорость кривошипа,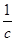 
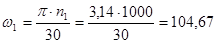
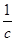
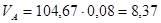
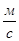
Для построения вектора скорости точки А определяем масштабный коэффициент
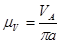(2.3)
где,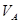 
- скорость точки А,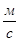 
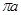- вектор скорости точки А,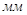
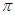- полюс, выбираемый произвольно
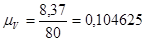
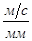
Для определения скорости точки B запишем систему уравнений:
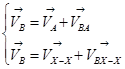(2.4)
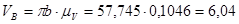
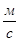
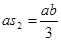- из задания
Для определения скорости центра масс 2-го звена S2 воспользуемся соотношением:
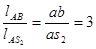(2.5)
где,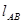 
, 
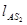- расстояния между соответствующими точками на механизме, м
, 
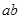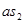- длинны векторов скоростей на плане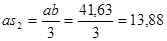, мм
мм
Соединив, точку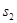 
и π получим скорость центра масс второго звена.
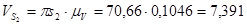
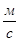
Для определения скорости точки C запишем систему уравнениё:
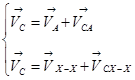(2.6)
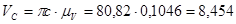
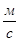
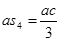- из задания
Для определения скорости центра масс 4-го звена S4 воспользуемся соотношением:
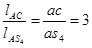(2.7)
где,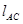 
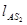, - расстояния между соответствующими точками на механизме, м
, 
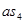- длинны векторов скоростей на плане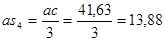, мм
мм
Соединив, точку 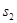и π получим скорость центра масс второго звена.
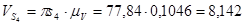
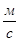
Определим значения угловых скоростей звеньев.
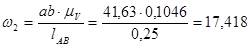
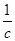
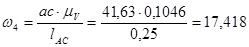
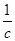
Направление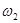 
определяем, перенеся вектор ab в точку S2 – второе звено вращается против часовой стрелки. Аналогично получим, что 
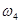направлена по часовой стрелке.
Скорости точек остальных положений определяются аналогичным образом. Все значения сводим в таблицу(2.1).
Таблица 2.1 – Значения линейных и угловых скоростей
| N положения | VB=VS3,
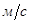
| VS2,
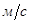
| VС=VS5,
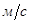
| VS4,
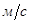
| VBA= VCA,
|  = ,
|
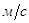
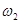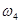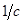
| 1 | 0 | 5,58 | 0 | 5,58 | 8,37 | 33,48 |
| 2 | 5,36 | 6,66 | 3,01 | 6,14 | 7,34 | 29,37 |
| 3 | 8,46 | 8,14 | 6,04 | 7,39 | 4,36 | 17,42 |
| 4 | 8,37 | 8,37 | 8,37 | 8,37 | 0 | 0 |
| 5 | 6,04 | 7,39 | 8,46 | 8,14 | 4,36 | 17,42 |
| 6 | 3,01 | 6,14 | 5,36 | 6,66 | 7,34 | 29,37 |
| 7 | 0 | 5,58 | 0 | 5,58 | 8,37 | 33,48 |
| 8 | 3,01 | 6,14 | 5,36 | 6,66 | 7,34 | 29,37 |
| 9 | 6,04 | 7,39 | 8,46 | 8,14 | 4,36 | 17,42 |
| 10 | 8,37 | 8,37 | 8,37 | 8,37 | 0 | 0 |
| 11 | 8,46 | 8,14 | 6,04 | 7,39 | 4,36 | 17,42 |
| 12 | 5,36 | 6,66 | 3,01 | 6,14 | 7,34 | 29,37 |
Определение ускорений
Определяем угловое ускорение звена 1.
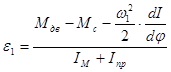, (3.1)
где,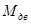 
- момент от сил движущих,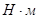 
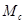- момент от сил сопротивления,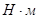
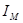- приведённый момент инерции маховика,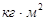 
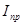- приведённый момент инерции рычажного механиз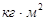ма для расчётного положения,
- первая производная от приведённого момента инерции механизма для расчётного положения
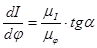, (3.2)
где,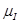 
- масштабный коэффициент по оси 
, 
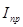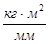
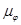- масштабный коэффициент по оси φ,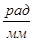 
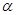- угол между касательной, проведённой к кривой графика 
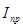в расчётном положении и осью φ.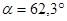 
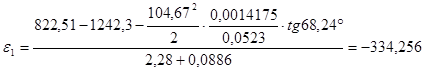
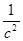
Знак минуса говорит о том, что кривошип ОА замедляется. Направляем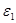 
против направления 
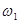и берём значение ускорения по модулю.
Строим план ускорений для расчётного положения.
Скорость точки А определяем по формуле
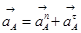, (3.3)
где,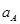 
- ускорение точки А, 
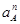- нормальное ускорение точки А относительно точки О,
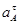- тангенциальное (касательное) ускорение точки А,
Ускорение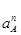 
найдём по формуле:
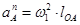, (3.4)
где,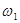 
- угловая скорость кривошипа,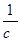 
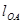- длина звена ОА, м
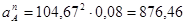
Ускорение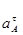 
найдём по формуле:
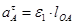, (3.5)
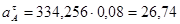
Из произвольно выбранного полюса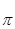 
откладываем вектор 
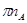длиной 100 мм. Найдём масштабный коэффициент плана скоростей.
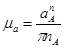, (3.6)
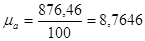
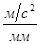
Определим длину вектора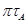 
:
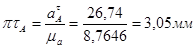
Ускорение точки А определим из следующеё формулы:
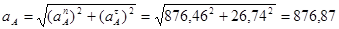
Определим ускорение точки B из следующей системы уравнений:
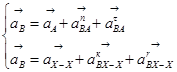, (3.7)
Для определения нормальных ускорений точки В относительно точек А и С
Воспользуемся следующими формулами:
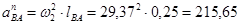
Определим длину векторов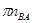 
:
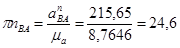
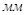
Ускорение направляющей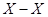 
равно нулю, т.к. она неподвижна.
Кореолисово ускорение точки В относительно направляющей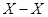 
рано нулю, т.к. точка В движется только поступательно относительно .
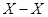Ускорение точки В найдём, решив системе (3.7) векторным способом:
Из вершины вектора ускорения точки А (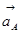 
) откладываем вектор 
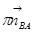(параллелен звену АВ и направлен от В к А), из вершины вектора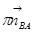
проводим прямую перпендикулярную звену АВ (линия действия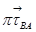 
); из полюса 
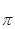проводим горизонтальную прямую (линия действия 
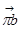); на пересечении линий действия векторов 
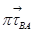и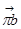 
получим точку b, соединив полученную точку с полюсом, получим вектор ускорения точки В.
Из плана ускорений определяем вектор ускорения точки В и вектор тангенциального ускорения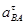 
:
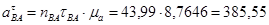
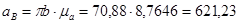
Ускорение сочки С определяем аналогично ускорению точки B.
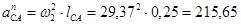
Определим длину векторов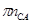 
:
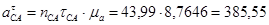
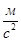
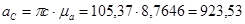
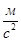
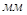
Из полученных тангенциальных ускорений найдём угловые ускорения 2-го и 3-го звеньев:
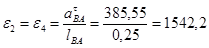
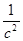
Определим ускорения центров масс звеньев:
Ускорение центра масс 2-го звена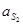 
найдём из соотношения (3.10)
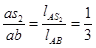(3.8)
Из плана ускорений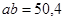 
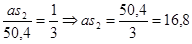мм
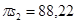мм
мм
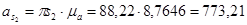
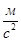
Ускорение центра масс 4-го звена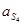 
найдём из соотношения (3.11)
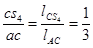(3.9)
Из плана ускорений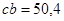 
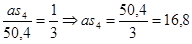мм
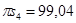мм
мм
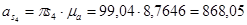
Ускорения центров масс 3-го и 5-го звеньев равны ускорениям точек D и D’ соответственно:
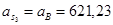
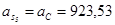
Значения всех ускорений сведём в таблицу:
Таблица 3.1 – Ускорения звеньев
| Ускорение точек механизма | Значение,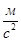
| Ускорение центров масс и угловые ускорения | значение, ,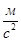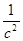 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
|
| 
| 
|
|
| 
| 
|
| 
| --- | --- |
| 
| --- | --- |
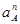
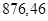
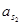
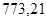
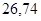
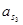
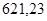
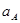
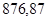
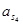
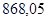
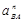
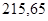
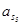
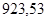
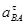
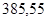
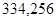
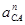
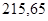
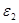
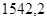
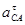
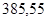
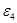
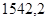
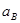
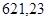
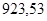
Определение углов давления
Найдём зависимость угла давления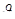 
от угла 
.
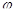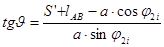(5.7)
где,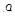 
- угол давления,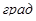 
- расстояние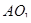 
, 
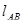- длина коромысла АВ,
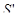- отрезок скорости,
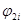- угол между отрезком АВ и расчётной прямой на чертеже,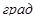 
Произведём расчёт при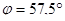 
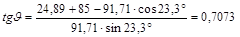
Остальные значения угла давления определяем аналогично, и результаты сносим в таблицу
Таблица 5.1 – Углы давления
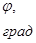
| 0 | 14,37 | 27,75 | 43,12 | 57,5 | 71,87 | 86,25 | 100,62 | 115 |
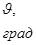
| -13,56 | 13,91 | 30,29 | 35,8 | 35,27 | 32,23 | 26,84 | 19,45 | 10,04 |
|
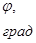
| 135 | 152,5 | 170 | 187,5 | 205 | 222,5 | 240 | 257,5 | 275 |
|
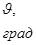
| 10,04 | -0,31 | -10,52 | -19,58 | -27,28 | -34,7 | -36,88 | -30,67 | -13,56 |
При построении используем следующие масштабные коэффициенты
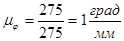
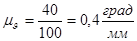
Литература
1. Артоболевский И.И. Теория механизмов и машин; Учеб. для втузов. – 4-е изд., перераб. и доп. – М.: Наука. 1988;
2. Девойно Г.Н. Курсовое проектирование по теории механизмов и машин. 1986.
КУРСОВОЙ ПРОЕКТ
на тему: «Механизмы компрессора»
Структурный анализ механизмов
Дата: 2019-07-24, просмотров: 264.
