Сегодня логика предстает во множестве модификаций, среди которых формальная логика Аристотеля, как она представлена преимущественно в «Органоне», рассматривается часто как одна из многих других. Эта аристотелевская, называемая также классической, логика пережила кульминационный пункт своего развития в схоластике,5 до этого же долгое время находилась в состоянии застоя. Христиан Вольф написал всеобъемлющую для XVIIIстолетия логику, одновременно выработав немецкую логическую терминологию, которая и до сего дня является основополагающей. Ни Кант, ни немецкие идеалисты — хотя Гегель и написал трехтомную «Науку логики» — не имели интереса к дальнейшему развитию формальной логики. Канта и Гегеля логика интересовала только как наука, истина которой основывалась на тождестве мышления и сущего. Так, раздел, названный в «Критике чистого разума» «Трансцендентальной логикой», занимающий более двух третей всей книги, трактует вопрос о возможности синтетических суждений apriori, т. е. вопрос о том, как возможно познание сущего. И в гегелевской логике тоже речь идет не о чистой
3 Кант И. Критика чистого разума. С. 82.
4 Там же. С. 83.
5 3десь следует особенно упомянуть Пьера Абеляра (1079-1142), Аверроэса (1126-1188), Альберта Великого (1183-1280), Петра Испанского (1208-1277), Уильяма Шервудского (Уильям из Шервуда, умер между 1266 и 1272) и Раймунда Луллия (1235-1315).
183
форме: здесь содержание мышления, сущее всегда уже в возможности совпадает с понятиями. Поэтому такая логика не подлежит тем ограничениям, которые Кант обозначил как признаки формальной логики. Последняя вновь получает сильный импульс для своего развития от Бернарда Больцано,6 но прежде всего от Джоржа Буля в произведении «TheMathematicalAnalysisofLogic, beinganEsseytowardsaCalculusofDeductiveReasoning». Затем Готлоб Фреге попытался обосновать математику логикой, что ему во многом удалось.7 Алфред Норт Уайтхед и Бертран Рассел издали трехтомное образцовое произведение по современной логике — «PrincipiaMathematica». С момента появления книги Рудольфа Карнапа8 «Очерк логистики» для новой логики, в отличие от традиционной, вводится название «Логистика».9 Логика исследует понятия, суждения и заключения, которые в свою очередь образуют всеобщие формы, где истинные результаты познания связаны друг с другом. Поскольку это так, то Кант был вправе утверждать в «Критике чистого разума», что логика имеет в себе критерии истины, даже если эти критерии по своему характеру негативны, т. е. если то, что им противоречит, никоим образом не может быть истинным. Тем не менее нас пока не должна занимать эта негативность, ибо независимо от вопроса, является ли истина согласием мышления с самим собой или это
6 Бернард Больцано родился в 1781 г. в Праге, там же и умер в 1848 г. Был профессором религиоведения на философском факультете университета Праги, правда, с 1820 г. ему было запрещено читать лекции. В XX столетии преимущественно благодаря своему «наукоучению» он рассматривается как предшественник современной логики. Важнейшие произведения: «Учебное пособие по религиоведению» (1834), «Наукоучение» (1837), в 1969 г. под редакцией Э. Винтера вышло «Собрание сочинений».
7 Готлоб Фридрих Людвиг Фреге (1848-1925), профессор логики и математики в Йене. Произведения: «Основы арифметики» (1884).
8 Рудольф Карнап родился в 1891 г. в Ронсдорфе. После изучения математики, физики и философии (1910-1914) в Йене, в 1926 г. стал доцентом философии в Вене и вошел в члены Венского кружка. В 1931 г. получил кафедру естествознания в Праге. В это время находился в тесном контакте с Морицем Шликом и Отто Нейратом, был знаком и с Витгенштейном. В конце 1935 г. эмигрировал в Америку, где преподавал вначале в Чикаго, а затем в Лос-Анжелесе. Умер в Санта-Монике (США) в 1970 г. Произведения: «Логическая конструкция мира» (1928), «Кажущиеся проблемы в философии» (1928), «Преодоление метафизики посредством логического анализа языка» (1931), «Логический синтаксис языка» (1934), «Основания логики и математики» (1939), «Исследования по семантике» (1942-1943), «Значение и необходимость» (1947), «Введение в символическую логику и ее приложения» (1958).
9 Предложение применять выражение «la logistique» в качестве названия новой логики было сделано, правда, не Карнапом, а исследователем Лейбница Луи Кутюра.
184
согласие свойственно только истине и таким образом является чисто негативной предпосылкой, а ведь негативные формальные предпосылки представляют собой условия, которые безусловно должны быть выполнены, истина должна быть высказываемой. Без сомнения, вывод не может быть истинным, если предпосылки, на которых он основывается, не истинны. С другой же стороны, заключение опять-таки может быть только тогда удовлетворительным, когда допустим способ связи, с помощью которого оно получено. Задача логики же состоит в том, чтобы находить и формулировать правила выведения, которые должны соблюдаться, когда стремятся прийти к удовлетворительным результатам и заключениям. При этом логика оперирует возможными «истинными значениями», т. е. следует исходить из того — идет ли речь о двойственной или множественной логике, — что высказывание, как и прежде, может быть истинным или нет; в случае же с тройственной логикой, например, нечто дополнительное по-прежнему бессмысленно. Правда, для способа такого логического установления истинного значения неважно, что в конечном счете означает «истинное».
В классической, т. е. двойственной логике, для которой существуют только два значения, а именно «истинное» или «ложное», оба этих значения соотносятся друг с другом как альтернативы. Чтобы пояснить это, мы обратимся к высказыванию: «Собор Святого Стефана находится в Вене». Это высказывание может быть истинным или ложным. Если оно ложно, то истинно высказывание «Собор Святого Стефана не находится в Вене». Обозначим первое высказывание как «р», второе—как «не-р» (р). Если принять для истинного и ложного буквы Wи F, то мы сможем отношение двух взаимоисключающих высказываний записать таким образом:
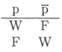
Если связать два высказывания друг с другом выводом, то мы должны, поскольку оба высказывания обладают истинным значением, задаться вопросом, каким образом истинное значение вывода, из связи которого возникает новое высказывание, соотносится с истинным значением связанного высказывания.10 Два связанных высказывания, часто называемые: одно — «функтор», второе—«юнктор», объединены. Эти функторы или юнкторы обозначаются как «и», «или», «если,
10 Ср.: Kamlah W., Lorenzen Р. Logische Propädeutik. Mannheim, 1973. S. 153.
185
то», «или, или». Это можно наглядно продемонстрировать на примере: остановимся на высказывании «Собор Святого Стефана находится в Вене, а Штутгарт является столицей земли Баден-Вюртемберг». Истинное значение этого высказывания зависит от истинного значения высказывания «Собор Святого Стефана находится в Вене» (р) и высказывания «Штутгарт является столицей земли Баден-Вюртенберг» (q). Юнктор «и», который связывает оба высказывания, исключается с помощью символа « 
». Применяя символический юнктор и знаки ρ и q, мы можем сказать:
Если истинно ρ и истинно q, то истинно 
Если ρ истинно, aq —ложно, или, соответственно, ρ ложно, aqистинно, то ложно также и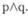 
Если ложно ρ и ложно q, то ложно также и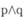 
Связь двух высказываний юнктором « 
» дает «конъюнкцию». Графически это выглядит так:
Это конъюнкция.
Наряду с конъюнкцией существуют дизъюнкция (pVq), импликация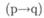 
, исключение 
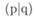и эквивалентность 
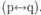. Примером дизъюнкции служит следующее высказывание: «Он ехал на автомобиле или на велосипеде». Это высказывание истинно, если одно из двух высказываний истинно (правда, немецкое слово «или» многозначно: если я говорю «Xявляется врачом или профессором», то это «или» допускает одно из двух, но в то же время то и другое). Импликация выражает отношение «если... то»: «Если Вена стоит на Дунае, то Гей-дельберг — на Неккаре». Импликция только тогда ложна, когда первое высказывание истинно, а второе — ложно, и она истинна, если первое высказывание ложно и второе также ложно. При исключении не могут быть одновременно истинными оба высказывания, примером тому может служить следующее предложение: «Ортлер — самая высокая гора в Австрии и Южном Тироле». Ортлер не может быть в двух местах, так как Южный Тироль отделен от Австрии, к тому же не является границей между ними. В исключении нет двух высказываний ни истинных, ни ложных. Эквивалентность в обиходе описывается подобно импликации словом «если» и часто подразумевает следующее:
186
«Ортлер является самой высокой горой Австрии в том случае, если Южный Тироль находится в Австрии». Другой пример звучит так: «Если день Святого Стефана (26 декабря) выпадает на воскресенье, то наступающий Новый год падает на субботу».
Логика построена на различных основоположениях, которые, хотя сами и не выведены, т. е. не доказаны, становятся в свою очередь предпосылкой выведения других предложений, так называемых теорем. Эти основоположения считаются в классической логике наиболее общими законами, которые имеют значение для всякого высказывания. В символической же логике или логистике, в противоположность этому, они считаются только базисными формами, из которых могут быть выведены все теоремы и к которым они могут быть сведены. Для классической логики основоположения являются безусловными и потому не требуют доказательства. Для современной логики они таковыми не представляются, и требуются доказательства для принятия решения об их эффективности как базисных форм. И далее, они для нее уже не единственные базисные формы. Есть еще и такие, которые имеют значение только в рамках этой логики.
ОСНОВОПОЛОЖЕНИЯ ЛОГИКИ
Существуют четыре основоположения:
1. Principiumidentitatis: А = А. Этот закон высказывает тождество чего-то с самим собой. В качестве логического требования рггпсгргит identitatisпритязает на то, чтобы любое понятие, любой символ применялся всегда в одном и том же значении.
2. Р riпс iр iит contradictionis: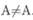 
. Этот закон противоречия, считающийся основным логическим законом, гласит о том, что в одном и том же высказывании невозможны одновременно утверждение и отрицание. Его формулировку мы находим — как уже упоминалось — в «Метафизике» Аристотеля, для которого этот закон представлялся онтологическим основоположением, а не просто логическим.
3. Principiumexclusitertii— закон исключенного третьего: В = А или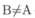 
— третьего не дано ( tertium поп datur). Это основоположение имеет значение в первую очередь для двойственной логики, для множественной же он имеет значение только в модифицированной форме: рггпсгргит exclusiquarti, quintiи так далее.
4. Principiumrationissufficientis — закон достаточного основания: в формулировке Лейбница он гласит: «никогда ничто не случается без
187
какой-либо причины или по крайней мере без достаточного основания».11
По своей структуре традиционная логика подразделяется на три отличных друг от друга части: на учение о понятии, учение о суждении и учение о заключении.
Давайте рассмотрим более подробно прежде всего формы, о которых трактует логика.
УЧЕНИЕ О ПОНЯТИИ
С вопросом, что такое понятие, мы уже сталкивались и при этом провели различие между сущностным и номинальным понятиями. Но мы говорили об унивокальных, эквивокальных и аналогичных понятиях. Под унивокальными понятиями, называемыми также синонимами, понимают разные понятия, которые имеют равное значение, тогда как омонимы являются эквивокальными понятиями, разное значение которых выражается одним и тем же словом. Аналогичные понятия выражают единство в различии и занимают в известном смысле среднее положение между унивокальными (идентичными по смыслу) и эквивокальными понятиями.
Далее, традиционная логика различает индивидуальные и универсальные понятия. Индивидуальные понятия —это имена, а именно имена собственные, которые сказываются об индивидуальном, которое не является общепознаваемым. Но вместо собственного имени могут применяться также и указующие признаки, такие как «этот здесь», «тот там»; например, когда я говорю: «Эта скрипка здесь». Имя «Сократ» означает то, что составляет индивидуальность Сократа, или понятие «греческий мир» подразумевает специфическое в имевшей в истории место греческой культуре. Другими индивидуальными понятиями являются «Дунай», «Рейн», «Неккар». Далее к индивидуальным понятиям причисляются также понятия отдельных вещей, таких как «скрипка, на которой я играл», «камень, о который я споткнулся». Индивидуум как таковой, соответственно отдельную вещь невозможно высказать с помощью универсального понятия, напротив, благодаря ему она может быть только описана; универсальные и всеобщие понятия высказывают об индивидууме лишь что-то. Предложение «Скрипка, на которой я играл» описывает совершенно определенный музыкальный инструмент. Но понятие «скрипка» как универсальное поня-
11 Лейбниц Г. В. Теодицея // Лейбниц Г В. Соч.: В 4 т. Т. 4. М., 1989. С. 157
188
тие не подразумевает лишь один конкретный экземпляр, именно тот, на котором я играл, а подразумевает множество экземпляров, которые принадлежат к определенному виду музыкальных инструментов. Вид музыкальных инструментов, к которым причисляются скрипки, можно определить понятийно, т. е. благодаря родовым характеристикам ( genusproximum). В случае со скрипкой родовое понятие —это «музыкальные инструменты», но ведь могли бы быть и «ударные инструменты», пока мы не выявили их отличительные признаки ( differentiaspecified). Таким образом, мы определяем универсальное понятие в логическом смысле с помощью родовой характеристики и отличительных признаков между понятиями на равной ступени: « definitiofitpergenusproximum et differentiamspecificam».
Отношение между видовыми и родовыми понятиями отчетливо видно на примере дерева Порфирия.12 Здесь следует заметить, что при отсутствии высшего родового понятия любое самое низшее видовое понятие может быть любым из этих понятий — как видовым, так и родовым.
Следующая схема изображает arborporphyrianaи заканчивается на индивидуумах и более не схватываемых в понятиях единичных ве-щах.13
Сам Порфирий описывает это дерево так:
Субстанция сама является также родом; но под нее подпадают тела, под тела — души тел, под которые подпадают чувствующие существа; а под чувствующие существа — разумные чувствующие существа, среди которых находится человек; среди людей наличествуют Сократ, Платон и другие конкретные люди.14
Понятия, говорили мы, следует определить. Но что значит определить? Определение, по-гречески horismos, не может быть словесным или реальным определением. Номинальное определение сводит одно понятие к другому. В нем одно понятие определяется с по-
12 Порфирий («Багряноносец») родился в 233 г. в Тире в Финикии и с 262 г. был учеником Плотина в Риме. Вначале он носил имя Мелек (король), затем сменил его на Базилевс, которое Плотин впоследствии превратил в Порфирия. Из Рима Порфирий уехал на Сицилию и в Карфаген, но после смерти Плотина (270 г.) вернулся назад в Рим, упорядочил его сочинения и руководил его школой, пока не умер в 304 г. Большая часть его сочинений утрачена, остались следующие: «Введение к „Категориям" Аристотеля», «Жизнь Плотина», «Жизнь Пифагора», «О пещере нимф».
13 Само «дерево» в нашем изображении, в противоположность наброску Порфирия, продолжено вплоть до единичного понятия.
14 Porphyries. Einleitung in die Kategorien. 2a.
|
|
| 189
|
190
мощью другого понятия. Так, например, Фома Аквинский утверждал, что определение бога Ансельмом как «то, больше чего нельзя себе представить»,15 есть чисто номинальная дефиниция,16 и это обособление ничего не говорит о существовании бога. Словесная дефиниция стремится объяснить понятие, исходя из его этимологии. Реальная дефиниция есть то, что в конечном счете является не просто объяснением названия, а объяснением вещи, «которое достаточно для знания объекта в его внутренних определениях, так как показывает возможность предмета из [его] внутренних призна-
17 КОВ». '
В плане реального определения как Аристотель, так и Кант учили, что понятие определяет сущее, хотя то, что ограничивается в определении понятием, выглядит отлично от него самого: для Аристотеля это что-бытие, ousiaсущего; трансцендентальная философия занималась не предметами, а способом познания предметов, выясняя, как он возможен apriori. То, что для него ограничено определением, поэтому также не может быть просто ousia, субстанцией, сущим, а, напротив, только способом данности сущего сознанию. В определении того, что дает понятие, отражается, как мы видим, различие новоевропейского и античного мышления.
Формальной же логики это различие не коснулось. Она исходит при формировании понятия из дефиниций, которые возникают или из уже существующего словоупотребления для понятия, или являются установками, которые возникают в результате применения понятия. Поэтому универсальные понятия в логике воспринимаются не как сущностные понятия в смысле реальной дефиниции, а как понятия имен или классов. Классы «есть расширение (объем) всеобщего понятия».18Примеры классов: жители Гейдельберга, чиновники, зеленые столы... Существуют классы отважных, депрессивных, зрителей, водителей автомобилей и так далее. На первом плане логического учения о понятии стоит объем понятия, называемый также расширением. При этом класс всех обозначений, который охватывает понятие, составляет его объем. Так, к объему понятия «музыкальные инструменты» принадлежат струнные инструменты, ударные инструменты, щипковые инструменты, духовые инструменты и так далее. Совокупность
15 Ансельм Кентерберийский. Прослогион // Ансельм Кентерберийский. Сочинения. М., 1995. С. 129.
16 Thomas von Aquin. Summa Theologica. I q.2 a. 1 ad 2.
17 Кант И. Логика // Кант И. Трактаты и письма. М., 1980. С.439.
18МеппеА. Einführung in die Logik. Bern; München, 1966. S. 73.
191
признаков, которые образуют понятие, представляет его содержание.19
УЧЕНИЕ О СУЖДЕНИИ
Что такое суждение? Кант в своей логике дает следующее определение:
Суждение есть представление единства сознания различных представлений или представление об их отношении, поскольку они образуют понятие.20
Он различает форму и материю суждения. Возьмем суждение «Это яблоко»: предмет «яблоко», о котором я говорю, составляет материю суждения, напротив, то, что сказывается об этом предмете «яблоко», а именно что он является яблоком, есть форма. С логической точки зрения форма соответствует понятию.
Таким образом, суждение — это предложение, которое выражает некий факт. А вопросы, просьбы, пожелания, приказы не являются суждениями. Для классической логики суждение возникает из связи понятий, а именно из понятия предиката и понятия субъекта. Коротко это выражается так: S= Р, яблоко спелое. Понятие предиката — это понятие, которое имеет больший объем: груши также могут быть спелыми. Суждение, которое не имеет формы S= Р, должно быть приведено к такой форме. Возьмем пример: выражение «Дерево приносит вкусные яблоки» означает, что дерево является приносящим вкусные яблоки. «Дерево» —это субъект (S), «приносящее вкусные яблоки» — предикат (Р), а «является» —это связка.
Уже в связи с освещением аристотелевских категорий мы указывали на кантовские категории и на то, что Кант формулировал их в соответствии с суждениями. Мы видели там, что суждения различаются в зависимости от своего количества, качества, отношения и модальности. Неясным остался вопрос, что является основанием этого различия.
Из логики мы теперь можем узнать, что количество суждения определяется отношением субъекта и предиката, в зависимости от того, полностью или частично включает или исключает понятие пре-
19 Со времен Фреге в современной логике содержание называется часто смыслом, а объем — значением понятия. О «понятии» см. также: Haller Ft. Begriff // Historisches Wörterbuch der Philosophie. Bd I. S. 780-785.
20 Кант И. Логика. С. 404.
192
диката понятие субъекта. Под количеством понимают объем действия связи, произведенной суждением. Она устанавливается как общая, особенная или единичная: суждение «Все цветы суть растения» является общим суждением; «Некоторые цветы плотоядные», в противоположность этому, особенное суждение. В первом случае понятие предиката признается в полном объеме для всех принадлежащих понятию субъекта предметов, во втором — только для некоторых. В единичном суждении отношение между субъектом и предикатом подобно отношению в общем суждении — предикат, согласно логической форме, как говорит Кант, «применяется» равнозначно общему. В нем понятие, не имеющее сферы, не имеющее объема, заключается как часть в сфере другого понятия. Пример такого суждения: «Цезарь смертен». Единичному суждению настолько же мало свойственно исключение, как и общему.
По качеству суждения бывают утвердительными, отрицательными или бесконечными. Примеры такого рода суждений мы находим в следующих высказываниях: «Цезарь есть курильщик», «Цезарь не есть курильщик», «Цезарь некурящий». В последнем, бесконечном суждении, которое, помимо прочего, так же как и единичное, не всеми логиками принимается за самостоятельное, отрицается в отличие от отрицательного суждения, не связка «есть», а понятие предиката курильщик: не-курящий. Само суждение является позитивным. Кант характеризизует его как суждение, в котором «субъект... полагается в сфере понятия, лежащего вне сферы другого».21 В бесконечном суждении субъект не содержится в сфере своего предиката, напротив,
он находится где-то вне ее22.
В утвердительном суждении понятие предиката принимается за понятие субъекта и приписывается ему; в отрицательном суждении понятие предиката отвергает понятие субъекта. В бесконечном суждении понятие предиката приписывается понятию субъекта, но само является отрицательным.
Согласно отношению различают категорические, гипотетические и дизъюнктивные суждения, при этом речь идет не только об отношении двух понятий. Гипотетическое суждение «Если — то» и дизъюнктивное «Или —или» исходят —в отличие от категорического суждения —
21 Там же. С. 406.
22Бесконечным суждением «за пределами конечной сферы А не определяется, под каким понятием содержится объект, но лишь то, что он относится к сфере вне А, каковая, собственно, и не есть сфера, а лишь ограничение сферы в бесконечном, или само ограничение» (там же).
193
уже не только из двух понятий. Предложение «Если — то» высказывает гипотетическое суждение со ссылкой на связь обоснования, в рамках которой действует то, что в гипотезе находится в предложении «если», а в выводе в предложении «то». Таким образом, в гипотетическом суждении два суждения связаны друг с другом как основание и вывод: «Если правительство избрано в результате свободных выборов, то оно с демократической точки зрения легитимно». Дизъюнктивное суждение характерно логической несвязностью разных возможных понятий предиката. Оно, как гипотетическое суждение, представляет некую взаимосвязь суждений, даже если отдельные члены дизъюнкции исключают друг друга: «Мир существует или благодаря слепому случаю, или внутренней необходимости, или внешней причине». В отличие от гипотетического и дизъюнктивного суждений, категорическое суждение образовано посредством только двух понятий: «Это правительство избрано свободно». В категорическом суждении не высказываются условия, т.е. ограничения, при которых оно действительно. Гипотетическое суждение называет условие своей действенности. В дизъюнктивном суждении называется множество взаимоисключающих условий возможного предиката. Отношение суждения выражает, таким образом, способ отношения между понятием субъекта и предиката.
Четвертый и последний вид суждения —это суждение модальности. В нем различаются проблематические, ассерторические и аподиктические суждения. Такие модальности сущего являются возможностью, действительностью и необходимостью, но они не дополняют определение объекта новым предикатом. Они характеризуют исключительно способ существования объекта. Если Кант в «Критике чистого разума» установил, что модальность нисколько не расширяет содержания понятия относительно его определения объекта, «а выражает только отношение к познавательной способности»,23 то здесь вновь проявляется отличное от античного и нововременного мышления понимание бытия. Примерами для трех видов модального суждения служат следующие: «Треугольник может быть прямоугольным». Это суждение по своему модусу является проблематическим суждением, ибо треугольник может быть также и тупоугольным. Ассерторическим является следующее суждение: «Этот треугольник имеет основание 8,5 см». Аподиктическое суждение: «Сумма углов треугольника должна составлять 180°». В такой форме суждения речь всегда идет
23 Кант И. Критика чистого разума. С. 281.
194
о способе действенности: связь между понятием субъекта и предиката действует возможным, действительным или необходимым образом.
УЧЕНИЕ О ЗАКЛЮЧЕНИИ
Под заключением понимают выведение одного суждения из другого. При этом важна не форма суждения, не его содержание, а исключительно форма связи различных суждений. Заключение трактует уже аристотелевская логика, гласящая в «Первой Аналитике» следующее:
. . силлогизм же есть речь, в которой, если нечто предложено, то с необходимостью вытекает нечто отличное от положенного в силу того, что
положенное есть24.
Как суждение есть связь понятий, так и заключение есть связь суждений. Вместе с тем заключение состоит из первых посылок, главных предложений ( propositio тагог), вторых посылок, второстепенных предложений ( propositiominor) и заключительного предложения (соп- clusio).25Общее для двух первых посылок понятие называется средним термином ( terminusmedius). Условием для связки суждений является то, что они содержат общее понятие, которое находит в них унивокальное применение. Два остальных понятия называют внешними терминами, а именно внешним термином в главном предложении, terminus тагог и внешним термином во второстепенном предложении, terminusminor. Как и прежде, место terminus тагог (Р, предикат), terminusmedius(Μ) и terminusminor(S, субъект) определяется четырьмя различными фигурами заключения:26
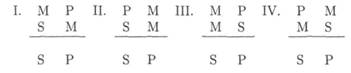
Учение о заключениях, силлогистика, имеет своей задачей гарантировать истинность выводов, т. е. то, что при принятии истинных посылок получаются истинные заключения. Но это не обязательно для всех возможных видов заключений, так что нужно опираться на правила заключений, важнейшие из которых звучат следующим образом:
24 Аристотель. Первая аналитика. С. 120.
25Обычно первая посылка оговаривается и называется главным предложением, которое содержит предикат заключительного предложения. За первой посылкой, содержащей субъект вывода, следует второстепенное предложение.
26Первые три выведены Аристотелем, четвертая — Калинусом. Их примеры приведены далее.
195
— Первые посылки нельзя отрицать в совокупности ( expurls пед- ativisnihilsequitur).
— Первые посылки не могут быть в совокупности частными предложениями ( expurlsparticularibusnihilsequitur).
— Если две первые посылки позитивны, то не последует негативного заключения (ambae affirmantes nequeunt generare negantem).
— Заключение нацелено на более сложные первые посылки (соп clusio sequitur partemdebiliorum).
Традиционная логика отныне занимается составлением заключений. Они формируются из суждений по приведенным ниже формам:
(а) все Sсуть Р (е) все Sсуть не Р (i) некоторые Sсуть Р (о) некоторые Sсуть не Р
а = общеутвердительным суждениям типа: «Все люди смертны», е = общеотрицательным суждениям типа: «Ни один человек не является богом».
i= частноутвердительным суждениям типа: «Некоторые морские животные млекопитающие».
о = частноотрицательным утверждениям типа: «Некоторые водные животные не являются жабродышащими».
а и i— обозначения affirmo(я утверждаю), е и о — обозначения nego(я отрицаю).
«Логический квадрат» должен продемонстрировать, каким образом различные формы суждения могут для заключения комбинироваться друг с другом и насколько они взаимно исключаются.
ЛОГИЧЕСКИЙ КВАДРАТ
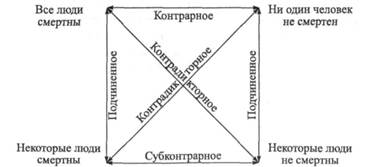
196
В случае комбинирования они образуют подчиненное отношение. В случае взаимного исключения получается контрарная, соответственно, субконтрарная, или контрадикторная, противоположность. Примером контрадикторной противоположности в логике служит: Р и не-Р (курильщик и некурящий). Здесь возникает противоположность благодаря утверждению и одновременному отрицанию одного и того же понятия. Белое и черное, жара и холод образуют контрарные противоположности: два разных понятия принадлежат иногда к одному и тому же роду. Субконтрарную противоположность мы находим в высказывании «Некоторые люди счастливы, некоторые люди несчастны». Подчиненное отношение — это соподчинение высказываний: «Все люди смертны, следовательно, Цезарь также смертен». Из логического квадрата мы теперь можем выяснить, какие комбинации а-, е-, i-, о-предложений дают действительный силлогизм.
Всего насчитывается 64 возможных вида заключения: от ааа, аае, aai... до ооо. Тем не менее на основе правил вывода можно рассматривать в качестве действительных только эти 12 модусов заключения. Помимо этого остаются следущие комбинации: ааа, aai, aee, aeo, aii, аоо, еае, еао, eio, iai, ieo, оао. Если мы модифицируем четыре фигуры заключения посредством этих 12 модусов заключения, то в совокупности получится 19 действительных фигур заключения. Для них есть ключевые слова, в которых гласные звуки а, е, i, о относятся к количеству и качеству первых посылок и выводов. Согласные в этих ключевых словах показывают, в каком заключении первой фигуры могут быть преобразованы в заключения трех других фигур заключения и какие шаги для этого преобразования следует сделать. (Sсогласно гласному звуку требует conversiosimplex, которое является смешением субъекта и предиката. Р требует conversioperaccidens, смешивания субъекта и предиката при преобразовании суждения а в суждение г, и соответственно, е в о. Если в ключевое слово вставить т, то потребуется metathesispraemissarum, т. е. смешение первых посылок. А с потребует conversiosyllogismi, т. е. косвенного доказательства.)
Начальные буквы ключевых слов, не принадлежащих к первой фигуре заключения, сообщают при этом, каким заключением первой фигуры может быть доказано значение.
Ключевые слова восходят к Петру Испанскому27 и сформулированы гекзаметром:
27 Петр Испанский родился между 1210 и 1220 г. в Лиссабоне. Был медиком и философом. Став Папой, взял имя Иоанн XXI. Умерв1277 г. вВиттербо.
197
I. Barbara, Celarent primae, Darii, Ferioque.
II. Cesare, Caemstrens, Festino, Baroco secundae.
III. Tertia grande sonans recital Darapti, Felapton, Disamis, Datisi, Bocardo, Ferison.
IV. Quartae sunt Bamalip, Calemes, Dimatis, Fesaro, Fresison.
Рассмотрим теперь фигуры заключения, чтобы попутно дать примеры преобразования.
/. Фигура:
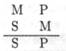
В этой фигуре можно сделать выводы согласно логическому квадрату в следующих комбинациях: ааа, eae, aii, eio.
Примером для фигуры заключения Barbara(ааа) будет: Все люди смертны. Все афиняне — люди. Следовательно, все афиняне смертны.
II. Фигура:
Для этой фигуры заключения возможны в следующих комбинациях: eae, aee, eio, аоо.
Примером для фигуры заключения Caemstres(aee) будет: Все лошади—непарнокопытные. Ни один вол не является непарнокопытным. Следовательно, ни один вол не является лошадью.
III. Фигура:
Здесь возможны следующие фигуры заключения: aai, aii, еао, eio, iai, оао.
Примером для фигуры заключения Darapti(aai) будет:
Все скрипки — смычковые инструменты.
Все скрипки — музыкальные инструменты.
Следовательно, некоторые музыкальные инструменты являются смычковыми инструментами.
198
IV. Фигура:
В этой фигуре могут быть получены заключения в соответствии со следующими комбинациями: aai, aee, iai, еао, eio. Примером для фигуры заключения Bamalip(aai) будет:
Все афиняне —люди.
Все люди смертны.
Следовательно, некоторые смертные — афиняне.
II, IIIи IVфигуры заключения сводимы к Iфигуре заключения и правило, которому здесь нужно следовать, называется соответствующим ключевым словом. Возьмем пример: модус Disamis(iai) IIIфигуры заключения нужно преобразовать в модус Iфигуры. Начальная буква Dуказывает на то, что модус Disamisследует свести к модусу Darii(aii) первой фигуры заключения. Модус Dariiимеет следующий вид:
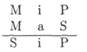
Sв ключевом слове Disamisв соответствии с iтребует для первой посылки conversiosimplex, т. е. ее следует преобразовать в Ρ iΜ. Μ показывает, что нужно предпринять перестановку посылок. Прежнее преобразование дало бы в качестве вывода Ρ iS. Последняя буква в названии Disamis, s, указывает на то, что также нужно предпринять conversiosimplexэтого вывода, так что в качестве результата получится: SiР. Тем самым мы получили силлогизм первой фигуры.
Логика не является теорией истины28 и не стремится ею быть. С отказом от знания содержания и ограничением своих исследований формой понятий, суждений и заключений она получает возможность позитивно говорить об истине. Для определения истины последовательность суждений и заключений может быть conditiosinequa поп, хотя истина не производится и не устанавливается логикой.
28 0 теорииистинысм.: Puntel L. В. Grundlagen einer Theorie der Wahrheit. Berlin; New York, 1990; Simon J. Wahrheit als Freiheit. Berlin; New York, 1978.
199
ЧТО ТАКОЕ ИСТИНА?
Дата: 2019-07-24, просмотров: 234.
