Пусть в банк B1 внесен вклад в S денежных единиц. Будем считать, что свободные резервы банка Bk (k=1,2,...,n-1) в результате ряда операций становятся вкладом в банк Bk+1 (k=1,2,...,n-1), а норма обязательных резервов установлена в p (0<p<100) процентов. Изменить ставку p так, чтобы суммарная величина кредитов, предоставляемых всеми банками, изменилась в a>0 (a¹1) раз, то есть либо увеличилась в a раз при a>1, либо уменьшилась в 1/a раз при 0<a<1.

Решение. Сразу отметим, что как и в предыдущей задаче не предполагается, что все банки Bk (k=1,2,...,n) различны. Задача, по-видимому, не всегда имеет решение. Если решение x есть, то как его искать? На помощь может прийти формула (40). В соответствии с ней имеем:

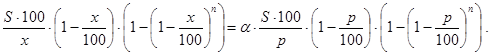
Сократим обе части этого соотношения на S×100 и, обозначив правую часть через b:

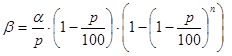
для нахождения решений задачи получим уравнение:

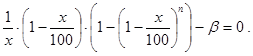 (41)

Последовательно преобразуем правую часть (41):

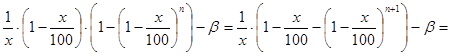
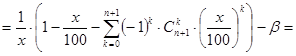
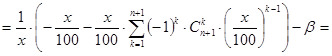
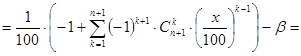
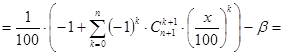
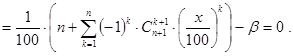
Следовательно, если x есть решение задачи, то его следует искать среди действительных корней многочлена g(t) (t=x/100) степени n, где

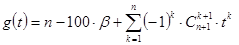 (42)

со следующим вектором коэффициентов:

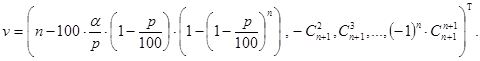 (43)

При этом, по смыслу задачи у многочлена (42) на промежутке (0,1) может быть не более одного корня t=x/100.

Таким образом, решение исходной задачи свелось к нахождению для многочлена g(t) c коэффициентами (43) действительного корня t: 0<t<1. Если такой корень отсутствует, то исходная задача решений не имеет, то есть, только за счет изменения текущей процентной ставки обязательных резервов изменить суммарную величину кредитов системы коммерческих банков в a раз не удастся. Если же корень tÎ(0,1) найден, то решением задачи является величина x=t×100. Иными словами, если назначить процентную ставку обязательных резервов в t×100 процентов, то суммарная величина кредитов измениться в a раз.

Решение исходной задачи может быть найдено с помощью функции times(n,p,a), обращающейся к следующим рекурсивным функциям: pow(a,n), C(n,m), binom2(n,k) и finroo(v). Ниже приведено краткое описание всех этих функций.

pow(a,n) - быстрое возведение действительного или комплексного числа a в целую неотрицательную степень n. Декомпозиция в рекурсии организована с помощью дихотомии - последовательными уменьшениями степени в два раза, то есть представлением a в виде:

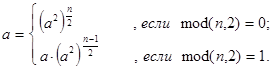
C(n,m) - вычисление количества сочетаний из n элементов по m элементов. Декомпозиция в рекурсии организована в соответствии с известной формулой: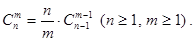

binom2(n,k) - вычисление последовательности биномиальных коэффициентов 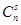 со знаком  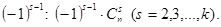Декомпозиция в рекурсии организована по величине аргумента s. База рекурсии соответствует значению s=2.

finroo(v) - нахождение в векторе v первой из компонент t, удовлетворяющей условию (Im(t) =0) ×(Re(t) Î(0,1)). Если таковых компонент не имеется, то возвращается значение, равное ¥. Декомпозиция в рекурсии организована по значению длины меняющегося вектора v.

times(n,p,a) - с помощью функций pow(), С() и binom2() находится вектор v коэффициентов (43) многочлена (42). После этого с использованием встроенной функции polyroots(v) отыскиваются корни многочлена (42). При написании программы-функции times(n,p,a) учтено утверждение критерия существования решения задачи, сформулированное ниже в виде леммы 1:

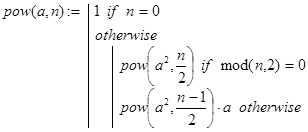
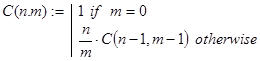
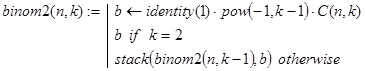
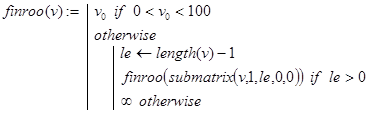
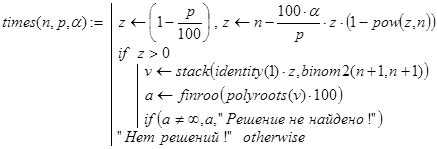
Замечание. Поскольку встроенная функция polyroots() находит значения корней приближенно, то даже при точных коэффициентах многочлена g(t) вместо корня tÎ(0,1) мы можем получить близкий к нему комплексный корень t1 с Re(t1) Î(0,1) и Im(t1) ¹0. Тогда функция times() сообщит об отсутствии решения исходной задачи. Но это может быть и не так. Поэтому получение такого сообщения требует более тщательного анализа корней многочлена (42). Например, искать требуемый вещественный корень в промежутке (0,1) с заданной степенью точности можно методом дихотомии. При этом следует исходить из следующего утверждения.

Лемма 1. Для существования решения исходной задачи необходима и достаточна положительность свободного члена многочлена (42), то есть выполнение условия g(0) >0. Иначе это условие можно записать в виде n>100×b или, по-другому,

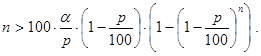
Доказательство. Необходимость. Пусть решение x исходной задачи существует. Тогда, как мы уже отмечали, его следует искать среди действительных корней многочлена g(t) (t=x/100 Î (0,1)). Нам понадобится значение g(t) в нуле: g(0) =n-100×b. Пусть t*Î(0,1) - корень g(t). В этом случае

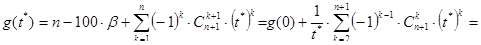
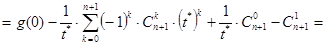
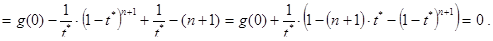 (44)

Но при любом t*Î(0,1) справедливо неравенство:

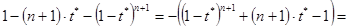
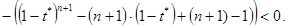 (45)

Последний переход в (45) сделан с использованием одного замечательного неравенства [13, c.24-27]:

xq - q×x + q -1 > 0 (x > 0, q > 1),

легко устанавливаемого с помощью методов дифференциального исчисления и являющегося основой для доказательства многих классических неравенств таких, например, как основные неравенства Гельдера и Минковского. Но тогда из (44) следует, что g(0) >0 и необходимость установлена.

Достаточность. Пусть выполнено условие g(0) >0. Подсчитаем значение функции g(t) в точке 1:

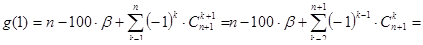
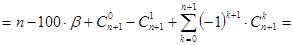
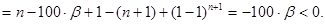
Последнее неравенство вместе с предположением g(0) >0 гарантирует наличие у многочлена g(t) действительного корня t*Î(0,1), а значит и решения x=t*×100 исходной задачи. Тем самым установлена достаточность, и лемма полностью доказана.

Дополнение 1 к задаче 19. Пусть банки Bk (k=1,2,...,n) функционируют так, как это описано в условиях задачи 19. Можно ли на r процентов (-100<r) изменить суммарную величину кредитов, предоставляемую банками? Если это возможно, то найти новую ставку обязательных резервов.

Решение. Заметим, что если r>0, то величина кредитов увеличивается, а если r<0, то она уменьшается. Далее, поскольку изменение суммарной величины кредитов на r процентов равносильно их изменению в 1+r/100 раз, то необходимо просто решать задачу 19 c a=(1+r/100). Условие существования решения (см. лемму 1) в данном случае запишется так:

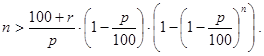
Дополнение 2 к задаче 19. Пусть банки Bk (k=1,2,...,n) функционируют так, как это описано в условиях задачи 19. Определить начальную процентную ставку p обязательных резервов, если её изменение до p1 процентов привело к изменению суммарной величины кредитов в b раз.

Решение. Согласно (40)

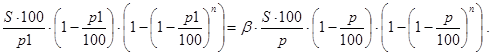
Если считать p неизвестным, то фактически мы опять имеем задачу 19, в которой требуется лишь заменить p на p1 и a на 1/b. Условие существования решения в данном случае запишется так:

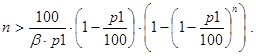
Завершая рассмотрение предложенного цикла задач, отметим, что большая часть из них допускает то или иное естественное обобщение и развитие.

Заключение

Рассмотрение затронутой в этой работе проблемы сейчас очень актуально, поэтому необходимо создание эффективных методик решения практических задач именно с помощью рекурсии, как одного из самых простых, понятных и наглядных методов решения задач. Реализация же рекурсивных алгоритмов в любой вычислительной среде достаточно очевидна, поэтому составление обучающих программ, реализация их в виде Web-узла и публикация их в Internet является очень полезным делом по вышеизложенным причинам. Продолжая освоение рекурсии в рамках данного или иного направления нелишне помнить слова выдающегося математика и педагога Д. Пойа [12, c.13]: “Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь. … Помните: если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их! ”. В вопросах освоения рекурсии именно так и нужно поступать. Только подражая хорошим образцам и постоянно практикуясь, можно освоить рекурсивный метод решения прикладных задач.

Литература

1. Симонов А.С. Экономика на уроках математики. М.: Школа-Пресс, 1999.

2. Борохов Э. Энциклопедия афоризмов (Мысль в слове). М.: изд. АСТ, 1999.

3. Дорофеев Г.В., Седова Е.А. Процентные вычисления. СПб.: Специальная литература, 1997.

4. Доллан Э.Д., Линдсей Д.Б. Рынок. Макроэкономическая модель. СПб., 1992.

5. Макконнелл К.Р., Брю С.Л. Экономикс. Т.1,2. М.: Республика, 1993.

6. Самуэльсон П. Экономика. Т.1,2. М.: Алгон, 1992.

7. Фишер С. и др. Экономика. М.: Алгон, 1992.

8. Ланкастер П. Теория матриц. М.: Наука, 1978.

9. Беллман Р. Введение в теорию матриц. М.: Наука, 1969.

10. Добровольский Н.М., Есаян А.Р., Пихтильков С. A., Стеценко В.Я. Об одном вычислительном эксперименте. Межвузовский сборник статей. Ч.1-Тула: Изд-во Тул. гос. пед. ун-та, 1999.10 с.

11. Есаян А.Р. Фракталы и рекурсия. Учеб. пособие для студентов педвузов. - Тула, 1999. -52с.

12. Пойа Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание. М.: Наука, 1970.

13. Беккенбах Э., Беллман Р. Неравенства. М.: Мир, 1965.

14. Вайскопф Дж. Microsoft FrontPage 2000: учебный курс - СПб.: Питер, 2000.