Вкладчик положил в сбербанк sum денежных единиц под pk (k=0. . n-1) процентов за каждый из n последующих периодов времени. В конце каждого периода k (k=0. . n-1) после начисления pk процентов он снимает со счета Ak денежных единиц. Иными словами, допускается, вообще говоря, и изменение процентной ставки, и величины денежных единиц, снимаемых с вклада. Составить программы, отвечающие на следующие вопросы:
Имеет ли задача решение?
Если задача имеет решение, то какова величина вклада после n периодов?
Если задача не имеет решения, то каков наименьший номер периода, в котором взятие соответствующей суммы оказалось невозможным?
Решение. Рассмотрим векторы процентных ставок и величин уменьшения вклада:
p=(p0,p1,…,pn-1) T, A=(A0,A1,…,An-1) T.
Ответ на первые два вопроса дают рекурсивные программы-функции waste2(sum,p,A) и waste3(sum,p,A). Если задача имеет решение, то они возвращают величину вклада после n периодов, а иначе - отрицательное число. Декомпозиция для функции waste2() проводилась, исходя из того же утверждения, что и для функции waste(), а декомпозиция для функции waste3() - исходя из того же утверждения, что и для функции waste1(). Во втором случае получена более компактная и ясная программа:
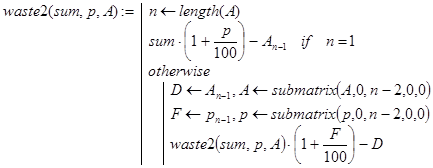
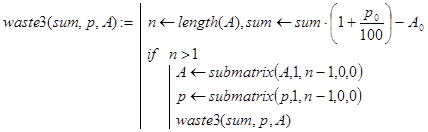
Наряду с этими программами можно вывести и конечную формулу wa(S,p,A) для расчетов. Пусть n=length(p). Тогда:
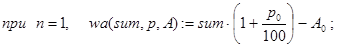
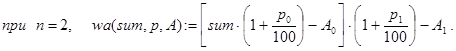
И, наконец, в общем случае:
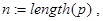
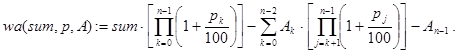
Контрольные примеры.
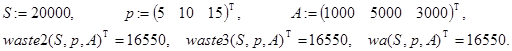
Попробуем теперь составить программу, отвечающую на третий из поставленных вопросов. Будем считать, что она должна возвращать вектор с двумя компонентами, который выглядит так:
[“O’key” решение] T, если задача имеет решение;
[период сальдо] T, если задача не имеет решения.
Во втором случае возвращается период (нумерация от 1 и далее) и отрицательное сальдо – количество денежных единиц, которых недостает для выплаты в данный период.
Всем перечисленным условиям удовлетворяет рекурсивная программа-функция waste4(sum,p,A,k):
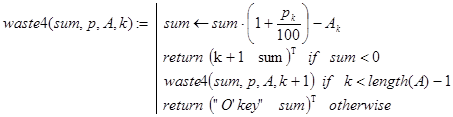
Здесь k - вспомогательный параметр. При первом обращении к waste4() его значение должно быть равно нулю. Далее k используется для организации рекурсивных вычислений, а операторы return - для прекращения рекурсивных вызовов при получении решения задачи.
Контрольные примеры.
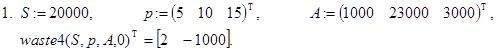
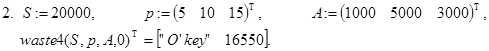
Дисконтирование. Инвестиции. Консолидирование
Задача о дисконтировании
Какую сумму следует внести сегодня в банк при процентной ставке p, чтобы через n периодов получить S денежных единиц?
Решение. Фактически речь идет о вычислении величины, называемой экономистами современной стоимостью отложенного платежа. Если положить в банк сумму в R=S/(1+p/100) n единиц, то через n периодов она превращается в S единиц. Та же самая сумма R через n-1 период превращается в S/(1+p/100) единиц. Таким образом, если discount(S,p,n) - решение исходной задачи, то при n¹0 имеем:
discount(S,p,n) = discount(S/(1+p/100),p,n-1).
Будем проводить рекурсию по количеству периодов n. Тогда последнее соотношение дает нам правило декомпозиции. Отсюда и получаем программу-функцию (5):
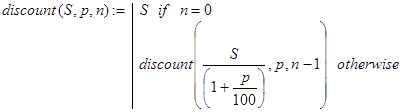 (5)
(5)
На вопросе о том, как проведена декомпозиция в (6), останавливаться не будем:
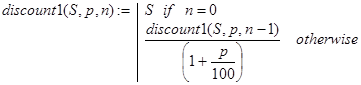 (6)
(6)
Замечание. Из проведенных рассуждений вытекает, что решение задачи может быть получено по конечной формуле:
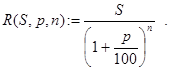
Контрольные примеры.

Задача о современной стоимости потока равных платежей.
Пусть реализация некоторого проекта обеспечивает поток равных платежей по S денежных единиц за каждый из n периодов при банковской ставке p процентов. Подсчитать современную стоимость этого потока.
Решение. Если просуммировать сегодняшнюю стоимость первого, второго и т.д. и, наконец, последнего платежа, то мы и получим современную стоимость всего потока. Пусть она равна payment(S,p,n). Тогда в силу задачи 6 о дисконтировании будем иметь:
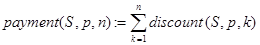
Впрочем, никто не мешает нам вывести и конечную формулу для расчетов, которая выглядит так:
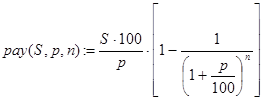
Однако мы займемся написанием рекурсивной программы-функции решения данной задачи. Выделить базу и провести декомпозицию наиболее просто, исходя из таких утверждений. Если n=0, то есть не прошло ни одного периода, то и платежей поступит 0. Далее, современная стоимость всех платежей - это современная стоимость платежей за первые n-1 период плюс современная стоимость последнего n-го платежа, равного S/(1+p/100) n. Отсюда и получаем функцию (7):
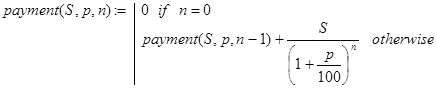 (7)
(7)
Другой вариант рекурсивной функции решения задачи 7 можно записать так:
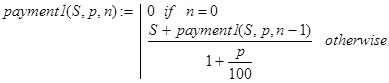 (8)
(8)
Контрольные примеры.
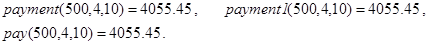
Дата: 2019-07-24, просмотров: 298.