План
Введение. 4
Динамика вклада. 7
Задача о величине вклада. 7
Задача о величине вклада после снятия денег в конце каждого периода 11
Задача о величине вклада после внесения (снятия) денег в конце или начале каждого периода. 13
Задача о изменяющихся процентных ставках. 15
Задача о изменяющихся процентных ставках и величинах снимаемых денег 16
Дисконтирование. Инвестиции. Консолидирование. 19
Задача о дисконтировании. 19
Задача о инвестировании проекта. 21
Задача о консолидировании платежей. 23
Платежи. 25
Задача о равных платежах в конце каждого периода. 25
Задача о платежах с одинаковой современной стоимостью.. 30
Задача о платежах на проценты.. 31
Разные задачи. 34
Задача о величине процентной ставки. 34
Задача о величине процентной ставки 2. 36
Задача о количестве периодов для расчета заемщика с банком.. 38
Задача о суммарной способности к кредитованию.. 41
Задача о минимальном количестве банков. 42
Задача о изменении величины суммарного кредитования. 43
Заключение. 50
Литература. 51
Введение
В электронные таблицы Excel, систему управления базами данных Access, язык программирования Visual Basic и многие другие современные компьютерные технологии встроены так называемые “финансовые функции”: fv(), pv(), pmt(), ppmt(), ipmt(), rate(), nper() и т.д. В повседневной жизни с задачами, в которых они могут быть использованы, приходится сталкиваться достаточно часто. Это заставляет преподавателей информатики педагогических вузов не только знакомить студентов различных специальностей с синтаксисом и семантикой этих функций, но и уделять особое внимание поиску новых методик и технологий обучения, ориентированных на прочное усвоение соответствующих знаний. И здесь на помощь может прийти рекурсия, с помощью которой строятся лаконичные и легко понимаемые алгоритмы, а затем и соответствующие информационные модели в виде рекурсивных программ на том или ином языке программирования [9, 10]. И что особенно важно, набор упомянутых финансовых функций и рекурсивные алгоритмы их вычисления могут служить весьма подходящим фоновым материалом для начального освоения студентами рекурсии как достаточно общего и эффективного метода решения практических задач.
Заметим, что вычисление значений финансовых функций с помощью электронных таблиц Excel или других пакетов прикладных программ можно признать целесообразным лишь при уже полностью сформированном понимании их синтаксиса и семантики. Но при первом знакомстве с этими и другими функциями рекурсивный подход в полной мере демонстрирует все свои дидактические преимущества по сравнению с простым описанием функций и решением по ним соответствующих прикладных задач. Он дает возможность не только всесторонне понять содержание излагаемого материала, но сделать это быстро и эффективно. И что особенно важно, полученные знания становятся достоянием долговременной памяти. Последний вывод убедительно подтверждается результатами проверочной работы, проведенной в двух группах студентов через год после ознакомления их с финансовыми функциями. Результаты эти оказались и удивительными, и убедительными. Более 36 процентов студентов, которым материал преподносился традиционно, с предъявленным заданием не справились. В то же самое время в группе, осваивавшей этот же материал с использованием рекурсии, с заданием не справились лишь 12 процентов студентов (3 человека). Столь разительное различие в уровне усвоения знаний в экспериментальной и контрольной группах заставляет нас по-новому оценить дидактические возможности рекурсии и осознать её роль и место в построении современного курса информатики в педагогических вузах. И эта роль, по-видимому, будет возрастать вместе с дальнейшим развитием компьютерной техники и программного обеспечения. В связи с этим главной задачей данной дипломной работы является разработка методик решения финансовых задач рекурсивными методами и их практическая реализация в виде обучающей программы (Web-узла) по данной теме.
При отборе материала для первоначального знакомства студентов и учащихся с рекурсивными методами решения прикладных задач, ориентированных на экономические специальности, существенную роль играют два фактора: наличие экономического содержания в этих задачах и прозрачность свойств рекурсивности рассматриваемых в них объектов. И то, и другое в полной мере может быть обеспечено рекурсивной реализацией финансовых функций.
Большой выбор содержательных задач, решаемых финансовыми функциями, можно встретить в сфере банковской деятельности [1,3-6]. Причем возникают они здесь на обслуживании всего лишь двух операций. Банк, являясь финансовым посредником между вкладчиками и заемщиками (рис.1), с одной стороны, принимает деньги и платит по ним проценты, а с другой стороны, дает кредиты и получает за них проценты. Разность между той суммой, которую получает банк от заемщиков по процентам за конкретный период, и той, которую он платит вкладчикам по процентам за этот же период, и составляет прибыль банка. Как говорил американский писатель-сатирик Генри Уилер Шоу [2, с.30] “Банковский процент не знает ни отдыха, ни богослужений, он работает и по ночам, и в воскресенье, и даже в дождливые дни”.
 |
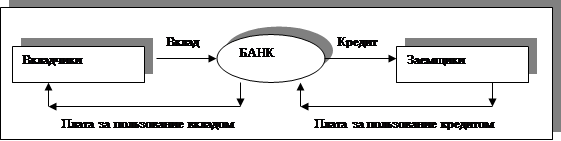Рис.1. Банк как финансовый посредник между вкладчиками и заемщиками
В рассматриваемой ниже серии задач везде речь идет об обычных вкладах и сложных процентах, а решения оформлены в виде рекурсивных программ-функций на языке программирования вычислительной среды Mathcad. Все они делятся на три категории: прямые рекурсивные аналоги, частные случаи и обобщения встроенных в Excel финансовых функций. Для первой категории функций и их аргументов используются стандартные обозначения. В иных ситуациях обозначения произвольны. Наличие почти во всех задачах несложно выводимой при определенных навыках, но обычно громоздкой, конечной формулы-решения позволяет на контрольных примерах легко проверить правильность составленных для них рекурсивных программ. Отметим, что все приведенные программы, благодаря рекурсивности, весьма просты и для их написания не требуется знания соответствующих конечных формул. В дополнении к данной работе дается краткое описание Mathcad и программы Microsoft FrontPage 2000, с помощью которой был создан Web-узел.
Динамика вклада
Начнем упомянутую серию задач с рассмотрения простой и многим знакомой житейской проблемы хранения денег в банке.
Задача о величине вклада
Вкладчик положил в банк сумму в sum денежных единиц под p процентов за один период времени (год, месяц, неделя и т.д.). Составить программу-функцию, возвращающую величину вклада по истечении n периодов времени (n = 1, 2, …).
Решение. Пусть invest(sum,p,n) - искомая функция. Вычисления значений invest() можно проводить по известной формуле:
invest(sum,p,n) = sum×(1+p/100) n.
Однако в учебных целях нас будет интересовать рекурсивный вариант алгоритма решения задачи. Её параметризация реализована в постановке. Рекурсию будем осуществлять по параметру n. База рекурсии очевидна. В самом деле, если вклад положен на хранение и взят сразу, то есть до истечения первого периода времени начисления процентов, то возврату подлежит начальная сумма вклада - sum. Далее, декомпозиция может быть реализована исходя из следующего факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на n – 1 период, взять и снова положить на 1 период. Соответствующий вариант программы-функции решения задачи выглядит так:
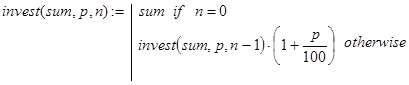(1)
Реализуя декомпозицию иным способом, получим другой вариант рекурсивной программы (1). Например, сделаем это исходя из такого факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на 1 период, взять и снова положить на n-1 период. Соответствующая программа-функция выглядит так:
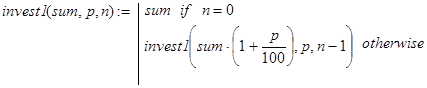(2)
В данной и подобной ей задачах указанные декомпозиционные посылки программно реализуются приблизительно с равной степенью сложности и, тем самым, обе имеют право на существование. Однако может возникнуть ситуация, когда предпочтение должно быть отдано той или иной конкретной посылке. Например, если в последующем имеется необходимость перейти к нерекурсивному варианту программы, то лучше пользоваться посылкой первого типа, а если есть проблемы с доказательством правильности реализуемого алгоритма, то целесообразно работать с посылкой второго типа.
Нетрудно видеть, что общее количество рекурсивных вызовов при вычислении invest(sum,p,n) и invest1(sum,p,n) равно n. Можно было бы уменьшить это значение до величины floor(log2(n)) +1, где floor(a) - целая часть натурального числа a, исходя из следующих двух декомпозиционных посылок.
Пусть сумма sum=m× g денежных единиц помещена на вклад при ставке в p процентов за период. Тогда через n периодов sum возрастет до той же самой величины, что и совокупная сумма m отдельных вкладов по g денежных единиц каждый, также помещенных под р процентов за период. Не ограничивая общности, величину sum можно считать целым неотрицательным числом. В противном случае можно было бы перейти к иному номиналу денежных единиц. Значения m и g также будем считать целыми числами.
Положить некоторую сумму sum в банк на n периодов – это то же самое, что положить эту сумму на k (0£k£n) периодов, взять и снова положить на n-k периодов.
Основанную на этих посылках рекурсивную функцию для решения задачи 1 обозначим через inv(sum,p,n). Указанные посылки обнаруживают такие свойства этой функции.
Первая посылка.
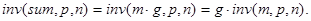
В частности, при m=1 получаем:
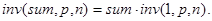
Первая и вторая посылки. Пусть k=floor(n/2), тогда.
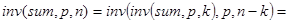
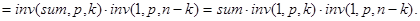
Отсюда при n=2×k сразу же получаем:
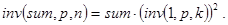
При n=2×k+1 имеем:
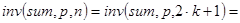
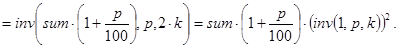
Выведенные соотношения для inv() позволяют записать такую программу для её вычисления:
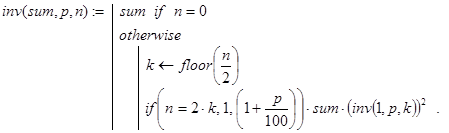
Общее количество рекурсивных вызовов при счете по этой программе-функции можно было бы подсчитать с помощью следующей вспомогательной рекурсивной функции:
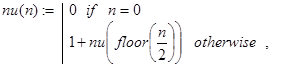
и оно действительно равно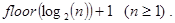 
Контрольные примеры.
Незначительная перестройка структуры функции inv(sum,p,n) позволяет получить еще один вариант её реализации, в котором количество рекурсивных вызовов в точности равно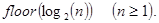 
Сделать это можно так:
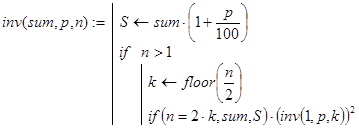
Замечание. В любых ситуациях, в которых возникают вопросы о быстродействии алгоритма, желательно по возможности минимизировать общее количество рекурсивных вызовов. В рассмотренной задаче построить алгоритм с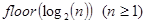 
рекурсивными вызовами можно было бы значительно проще, исходя из конечной формулы для решения задачи и дихотомии. Однако путь, который мы прошли, имеет свои достоинства. Он позволяет в общем случае выявить ограничения на рекурсивную функцию, достаточные для столь малого количества рекурсивных обращений при её вычислении. Фактически, из проведенных рассуждений вытекает такое утверждение.
Пусть функция F(a,n,v) удовлетворяет условиям:
F(a,1,v) =g(a,v),
F(a,n,v) =a×F(1,n,v),
F(a,n,v) =F(F(a,k,v),n-k,v) (1£k£n),
где a - действительное число, n - натуральное число, v=(v1,v2,…,vs) T - вектор с числовыми компонентами, g(a,v) - функция, значения которой для a и v из области определения F(a,n,v) мы вычислять можем. Тогда рекурсивная программа-функция:
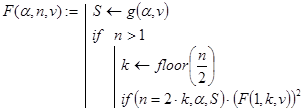
вычисляет значение F(a,n,v) ровно за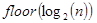 
рекурсивных вызовов.
Доказательство этого факта с использованием свойств A, B и C можно провести так:
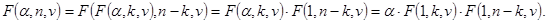
Отсюда, при n=2×k имеем
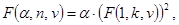
а при n=2×k+1 получаем
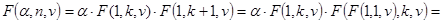
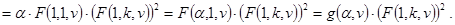
Именно на этих соотношениях и базируется алгоритм, реализуемый программой-функцией F(a,n,v).
И в заключение замечания приведем пример функции, удовлетворяющей условиям A, B и С: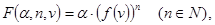 
где в области определения функции f(v) её значения мы вычислят умеем.
Задача о дисконтировании
Какую сумму следует внести сегодня в банк при процентной ставке p, чтобы через n периодов получить S денежных единиц?
Решение. Фактически речь идет о вычислении величины, называемой экономистами современной стоимостью отложенного платежа. Если положить в банк сумму в R=S/(1+p/100) n единиц, то через n периодов она превращается в S единиц. Та же самая сумма R через n-1 период превращается в S/(1+p/100) единиц. Таким образом, если discount(S,p,n) - решение исходной задачи, то при n¹0 имеем:
discount(S,p,n) = discount(S/(1+p/100),p,n-1).
Будем проводить рекурсию по количеству периодов n. Тогда последнее соотношение дает нам правило декомпозиции. Отсюда и получаем программу-функцию 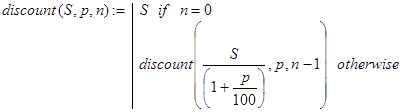(5):
(5)
На вопросе о том, как проведена декомпозиция в (6), останавливаться не будем:
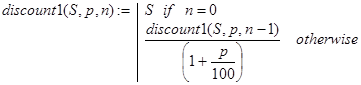(6)
Замечание. Из проведенных рассуждений вытекает, что решение задачи может быть получено по конечной формуле:
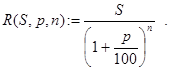
Контрольные примеры.
Задача о современной стоимости потока равных платежей.
Пусть реализация некоторого проекта обеспечивает поток равных платежей по S денежных единиц за каждый из n периодов при банковской ставке p процентов. Подсчитать современную стоимость этого потока.
Решение. Если просуммировать сегодняшнюю стоимость первого, второго и т.д. и, наконец, последнего платежа, то мы и получим современную стоимость всего потока. Пусть она равна payment(S,p,n). Тогда в силу задачи 6 о дисконтировании будем иметь:
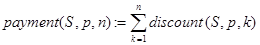
Впрочем, никто не мешает нам вывести и конечную формулу для расчетов, которая выглядит так:
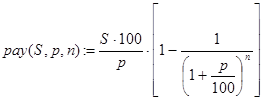
Однако мы займемся написанием рекурсивной программы-функции решения данной задачи. Выделить базу и провести декомпозицию наиболее просто, исходя из таких утверждений. Если n=0, то есть не прошло ни одного периода, то и платежей поступит 0. Далее, современная стоимость всех платежей - это современная стоимость платежей за первые n-1 период плюс современная стоимость последнего n-го платежа, равного S/(1+p/100) n. Отсюда и получаем функцию 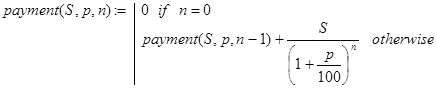(7):
(7)
Другой вариант рекурсивной функции решения задачи 7 можно записать так:
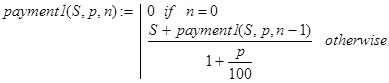(8)
Контрольные примеры.
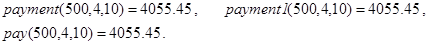
Платежи
Разные задачи
Заключение
Рассмотрение затронутой в этой работе проблемы сейчас очень актуально, поэтому необходимо создание эффективных методик решения практических задач именно с помощью рекурсии, как одного из самых простых, понятных и наглядных методов решения задач. Реализация же рекурсивных алгоритмов в любой вычислительной среде достаточно очевидна, поэтому составление обучающих программ, реализация их в виде Web-узла и публикация их в Internet является очень полезным делом по вышеизложенным причинам. Продолжая освоение рекурсии в рамках данного или иного направления нелишне помнить слова выдающегося математика и педагога Д. Пойа [12, c.13]: “Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь. … Помните: если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их! ”. В вопросах освоения рекурсии именно так и нужно поступать. Только подражая хорошим образцам и постоянно практикуясь, можно освоить рекурсивный метод решения прикладных задач.
Литература
1. Симонов А.С. Экономика на уроках математики. М.: Школа-Пресс, 1999.
2. Борохов Э. Энциклопедия афоризмов (Мысль в слове). М.: изд. АСТ, 1999.
3. Дорофеев Г.В., Седова Е.А. Процентные вычисления. СПб.: Специальная литература, 1997.
4. Доллан Э.Д., Линдсей Д.Б. Рынок. Макроэкономическая модель. СПб., 1992.
5. Макконнелл К.Р., Брю С.Л. Экономикс. Т.1,2. М.: Республика, 1993.
6. Самуэльсон П. Экономика. Т.1,2. М.: Алгон, 1992.
7. Фишер С. и др. Экономика. М.: Алгон, 1992.
8. Ланкастер П. Теория матриц. М.: Наука, 1978.
9. Беллман Р. Введение в теорию матриц. М.: Наука, 1969.
10. Добровольский Н.М., Есаян А.Р., Пихтильков С. A., Стеценко В.Я. Об одном вычислительном эксперименте. Межвузовский сборник статей. Ч.1-Тула: Изд-во Тул. гос. пед. ун-та, 1999.10 с.
11. Есаян А.Р. Фракталы и рекурсия. Учеб. пособие для студентов педвузов. - Тула, 1999. -52с.
12. Пойа Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание. М.: Наука, 1970.
13. Беккенбах Э., Беллман Р. Неравенства. М.: Мир, 1965.
14. Вайскопф Дж. Microsoft FrontPage 2000: учебный курс - СПб.: Питер, 2000.
План
Введение. 4
Динамика вклада. 7
Задача о величине вклада. 7
Задача о величине вклада после снятия денег в конце каждого периода 11
Задача о величине вклада после внесения (снятия) денег в конце или начале каждого периода. 13
Задача о изменяющихся процентных ставках. 15
Задача о изменяющихся процентных ставках и величинах снимаемых денег 16
Дисконтирование. Инвестиции. Консолидирование. 19
Задача о дисконтировании. 19
Задача о инвестировании проекта. 21
Задача о консолидировании платежей. 23
Платежи. 25
Задача о равных платежах в конце каждого периода. 25
Задача о платежах с одинаковой современной стоимостью.. 30
Задача о платежах на проценты.. 31
Разные задачи. 34
Задача о величине процентной ставки. 34
Задача о величине процентной ставки 2. 36
Задача о количестве периодов для расчета заемщика с банком.. 38
Задача о суммарной способности к кредитованию.. 41
Задача о минимальном количестве банков. 42
Задача о изменении величины суммарного кредитования. 43
Заключение. 50
Литература. 51
Введение
В электронные таблицы Excel, систему управления базами данных Access, язык программирования Visual Basic и многие другие современные компьютерные технологии встроены так называемые “финансовые функции”: fv(), pv(), pmt(), ppmt(), ipmt(), rate(), nper() и т.д. В повседневной жизни с задачами, в которых они могут быть использованы, приходится сталкиваться достаточно часто. Это заставляет преподавателей информатики педагогических вузов не только знакомить студентов различных специальностей с синтаксисом и семантикой этих функций, но и уделять особое внимание поиску новых методик и технологий обучения, ориентированных на прочное усвоение соответствующих знаний. И здесь на помощь может прийти рекурсия, с помощью которой строятся лаконичные и легко понимаемые алгоритмы, а затем и соответствующие информационные модели в виде рекурсивных программ на том или ином языке программирования [9, 10]. И что особенно важно, набор упомянутых финансовых функций и рекурсивные алгоритмы их вычисления могут служить весьма подходящим фоновым материалом для начального освоения студентами рекурсии как достаточно общего и эффективного метода решения практических задач.
Заметим, что вычисление значений финансовых функций с помощью электронных таблиц Excel или других пакетов прикладных программ можно признать целесообразным лишь при уже полностью сформированном понимании их синтаксиса и семантики. Но при первом знакомстве с этими и другими функциями рекурсивный подход в полной мере демонстрирует все свои дидактические преимущества по сравнению с простым описанием функций и решением по ним соответствующих прикладных задач. Он дает возможность не только всесторонне понять содержание излагаемого материала, но сделать это быстро и эффективно. И что особенно важно, полученные знания становятся достоянием долговременной памяти. Последний вывод убедительно подтверждается результатами проверочной работы, проведенной в двух группах студентов через год после ознакомления их с финансовыми функциями. Результаты эти оказались и удивительными, и убедительными. Более 36 процентов студентов, которым материал преподносился традиционно, с предъявленным заданием не справились. В то же самое время в группе, осваивавшей этот же материал с использованием рекурсии, с заданием не справились лишь 12 процентов студентов (3 человека). Столь разительное различие в уровне усвоения знаний в экспериментальной и контрольной группах заставляет нас по-новому оценить дидактические возможности рекурсии и осознать её роль и место в построении современного курса информатики в педагогических вузах. И эта роль, по-видимому, будет возрастать вместе с дальнейшим развитием компьютерной техники и программного обеспечения. В связи с этим главной задачей данной дипломной работы является разработка методик решения финансовых задач рекурсивными методами и их практическая реализация в виде обучающей программы (Web-узла) по данной теме.
При отборе материала для первоначального знакомства студентов и учащихся с рекурсивными методами решения прикладных задач, ориентированных на экономические специальности, существенную роль играют два фактора: наличие экономического содержания в этих задачах и прозрачность свойств рекурсивности рассматриваемых в них объектов. И то, и другое в полной мере может быть обеспечено рекурсивной реализацией финансовых функций.
Большой выбор содержательных задач, решаемых финансовыми функциями, можно встретить в сфере банковской деятельности [1,3-6]. Причем возникают они здесь на обслуживании всего лишь двух операций. Банк, являясь финансовым посредником между вкладчиками и заемщиками (рис.1), с одной стороны, принимает деньги и платит по ним проценты, а с другой стороны, дает кредиты и получает за них проценты. Разность между той суммой, которую получает банк от заемщиков по процентам за конкретный период, и той, которую он платит вкладчикам по процентам за этот же период, и составляет прибыль банка. Как говорил американский писатель-сатирик Генри Уилер Шоу [2, с.30] “Банковский процент не знает ни отдыха, ни богослужений, он работает и по ночам, и в воскресенье, и даже в дождливые дни”.
| |
Рис.1. Банк как финансовый посредник между вкладчиками и заемщиками
В рассматриваемой ниже серии задач везде речь идет об обычных вкладах и сложных процентах, а решения оформлены в виде рекурсивных программ-функций на языке программирования вычислительной среды Mathcad. Все они делятся на три категории: прямые рекурсивные аналоги, частные случаи и обобщения встроенных в Excel финансовых функций. Для первой категории функций и их аргументов используются стандартные обозначения. В иных ситуациях обозначения произвольны. Наличие почти во всех задачах несложно выводимой при определенных навыках, но обычно громоздкой, конечной формулы-решения позволяет на контрольных примерах легко проверить правильность составленных для них рекурсивных программ. Отметим, что все приведенные программы, благодаря рекурсивности, весьма просты и для их написания не требуется знания соответствующих конечных формул. В дополнении к данной работе дается краткое описание Mathcad и программы Microsoft FrontPage 2000, с помощью которой был создан Web-узел.
Динамика вклада
Начнем упомянутую серию задач с рассмотрения простой и многим знакомой житейской проблемы хранения денег в банке.
Задача о величине вклада
Вкладчик положил в банк сумму в sum денежных единиц под p процентов за один период времени (год, месяц, неделя и т.д.). Составить программу-функцию, возвращающую величину вклада по истечении n периодов времени (n = 1, 2, …).
Решение. Пусть invest(sum,p,n) - искомая функция. Вычисления значений invest() можно проводить по известной формуле:
invest(sum,p,n) = sum×(1+p/100) n.
Однако в учебных целях нас будет интересовать рекурсивный вариант алгоритма решения задачи. Её параметризация реализована в постановке. Рекурсию будем осуществлять по параметру n. База рекурсии очевидна. В самом деле, если вклад положен на хранение и взят сразу, то есть до истечения первого периода времени начисления процентов, то возврату подлежит начальная сумма вклада - sum. Далее, декомпозиция может быть реализована исходя из следующего факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на n – 1 период, взять и снова положить на 1 период. Соответствующий вариант программы-функции решения задачи выглядит так:
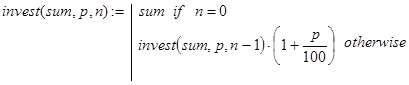(1)
Реализуя декомпозицию иным способом, получим другой вариант рекурсивной программы (1). Например, сделаем это исходя из такого факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на 1 период, взять и снова положить на n-1 период. Соответствующая программа-функция выглядит так:
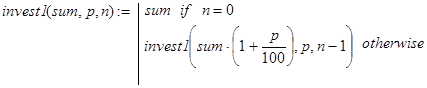(2)
В данной и подобной ей задачах указанные декомпозиционные посылки программно реализуются приблизительно с равной степенью сложности и, тем самым, обе имеют право на существование. Однако может возникнуть ситуация, когда предпочтение должно быть отдано той или иной конкретной посылке. Например, если в последующем имеется необходимость перейти к нерекурсивному варианту программы, то лучше пользоваться посылкой первого типа, а если есть проблемы с доказательством правильности реализуемого алгоритма, то целесообразно работать с посылкой второго типа.
Нетрудно видеть, что общее количество рекурсивных вызовов при вычислении invest(sum,p,n) и invest1(sum,p,n) равно n. Можно было бы уменьшить это значение до величины floor(log2(n)) +1, где floor(a) - целая часть натурального числа a, исходя из следующих двух декомпозиционных посылок.
Пусть сумма sum=m× g денежных единиц помещена на вклад при ставке в p процентов за период. Тогда через n периодов sum возрастет до той же самой величины, что и совокупная сумма m отдельных вкладов по g денежных единиц каждый, также помещенных под р процентов за период. Не ограничивая общности, величину sum можно считать целым неотрицательным числом. В противном случае можно было бы перейти к иному номиналу денежных единиц. Значения m и g также будем считать целыми числами.
Положить некоторую сумму sum в банк на n периодов – это то же самое, что положить эту сумму на k (0£k£n) периодов, взять и снова положить на n-k периодов.
Основанную на этих посылках рекурсивную функцию для решения задачи 1 обозначим через inv(sum,p,n). Указанные посылки обнаруживают такие свойства этой функции.
Первая посылка.
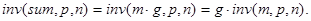
В частности, при m=1 получаем:
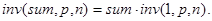
Первая и вторая посылки. Пусть k=floor(n/2), тогда.
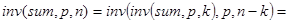
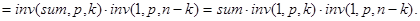
Отсюда при n=2×k сразу же получаем:
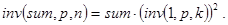
При n=2×k+1 имеем:
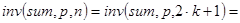
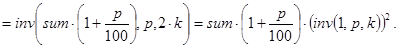
Выведенные соотношения для inv() позволяют записать такую программу для её вычисления:
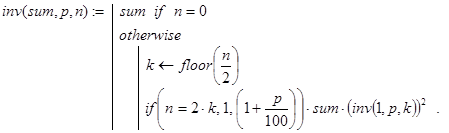
Общее количество рекурсивных вызовов при счете по этой программе-функции можно было бы подсчитать с помощью следующей вспомогательной рекурсивной функции:
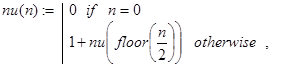
и оно действительно равно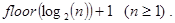
Контрольные примеры.
Незначительная перестройка структуры функции inv(sum,p,n) позволяет получить еще один вариант её реализации, в котором количество рекурсивных вызовов в точности равно 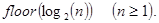Сделать это можно так:
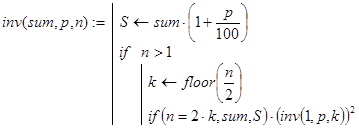
Замечание. В любых ситуациях, в которых возникают вопросы о быстродействии алгоритма, желательно по возможности минимизировать общее количество рекурсивных вызовов. В рассмотренной задаче построить алгоритм с 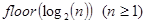рекурсивными вызовами можно было бы значительно проще, исходя из конечной формулы для решения задачи и дихотомии. Однако путь, который мы прошли, имеет свои достоинства. Он позволяет в общем случае выявить ограничения на рекурсивную функцию, достаточные для столь малого количества рекурсивных обращений при её вычислении. Фактически, из проведенных рассуждений вытекает такое утверждение.
Пусть функция F(a,n,v) удовлетворяет условиям:
F(a,1,v) =g(a,v),
F(a,n,v) =a×F(1,n,v),
F(a,n,v) =F(F(a,k,v),n-k,v) (1£k£n),
где a - действительное число, n - натуральное число, v=(v1,v2,…,vs) T - вектор с числовыми компонентами, g(a,v) - функция, значения которой для a и v из области определения F(a,n,v) мы вычислять можем. Тогда рекурсивная программа-функция:
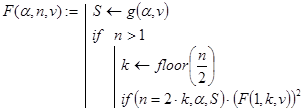
вычисляет значение F(a,n,v) ровно за 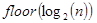рекурсивных вызовов.
Доказательство этого факта с использованием свойств A, B и C можно провести так:
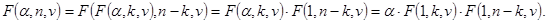
Отсюда, при n=2×k имеем
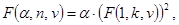
а при n=2×k+1 получаем
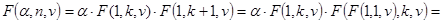
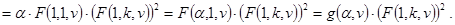
Именно на этих соотношениях и базируется алгоритм, реализуемый программой-функцией F(a,n,v).
И в заключение замечания приведем пример функции, удовлетворяющей условиям A, B и С: 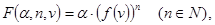где в области определения функции f(v) её значения мы вычислят умеем.
Задача о величине вклада после снятия денег в конце каждого периода
Вкладчик положил в банк сумму в sum денежных единиц под p процентов за один период времени. В конце каждого периода вкладчик после начисления процентов снимает со счета A денежных единиц. Определить сумму вклада через n периодов времени.
Решение. Данная задача весьма похожа на задачу 1. Рекурсивная программа-функция waste(sum,p,A,n) реализует декомпозицию, исходя из такого утверждения. Положить сумму sum в банк на n периодов со снятием в конце каждого периода по A денежных единиц – это то же самое, что положить данную сумму на тех же условиях на n – 1 период, взять, снова положить на 1 период и затем снять A единиц.
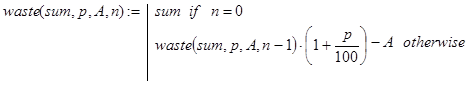(3)
Нетрудно понять, на какую посылку опирается при декомпозиции рекурсивная программа-функция waste1(sum,p,A,n), решающая ту же самую задачу о динамике вклада.
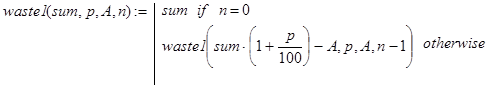(4)
Замечание 1. Конечная формула для решения задачи 2 выглядит так:
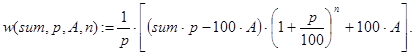
Выводится она следующим образом.
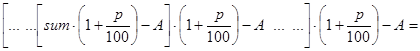
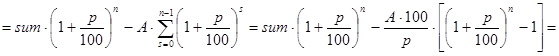
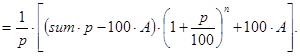
Одно из преимуществ “формул” waste() и waste1() в том, что они выписываются без всякого вывода и практически без затруднений.
Контрольные примеры.
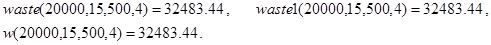
Замечание 2. В связи с задачей о динамике вклада может быть поставлен и такой вопрос. Сколько лет подряд вкладчик может снимать со счета по A денежных единиц в конце каждого периода после начисления процентов, если он положил в банк сумму в S единиц при ставке p процентов. Ответ на него может дать рекурсивная функция year(S,p,A):
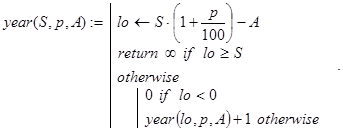
Здесь случай неубывания величины вклада выделен отдельно (lo³S), рекурсия организована по остаткам вклада после периодов, в которых хватило денег на очередную выплату в A единиц.
Контрольные примеры.
Дата: 2019-07-24, просмотров: 180.
