Місто StatVillage
StatVillage – це гіпотетичне місто, яке складається з окремих домогосподарств і використовується як база даних для студентів та аспірантів, що вивчають вибіркові методи.
Дані домогосподарств для StatVillage обирались навмання з результатів перепису сімей, що мешкали в домогосподарствах у місті Ванкувері, Британській Колумбії, Канаді у 1991 році. Сам перепис населення проходив шляхом анонімного анкетування. Бралися до уваги наступні характеристики:
· демографічні показники – розмір домогосподарства та його склад за віком та статтю;
· показники доходу – зайнятість, інвестиції, валові витрати, різні доходи домогосподарств та інші;
· житлові характеристики – тип житла, рік побудови, своє житло чи орендоване, оціночна вартість, щомісячні витрати на розміщення та інші;
· характеристика двох головних членів сім’ї, які відповідають за добробут сім’ї – вік, стать, професія, рідна мова, освіта, зайнятість і т.д;
Існують три конфігурації міста StatVillage:
· Maximal village – складається зі 128 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств - 1024).
· Mini village – складається з 60 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств – 480).
· Micro village – складається з 36 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств – 288).
Кожен блок домогосподарств нумерується в певному порядку, а саме
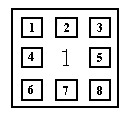
Рис. 2.1.1 Нумерування блоку домогосподарств
Для того, щоб отримати дані з міста StatVillage, необхідно спочатку відмітити домогосподарства позначкою як показано на рисунку 2.1.2 (відмічено кожне 8-ме домогосподарство)
Рис. 2.1.2 Систематичної вибірка кожного восьмого домогосподарства
Після цього натискаємо кнопку «Get the sample units» і отримуємо код, який представлений на рис. 2.1.3
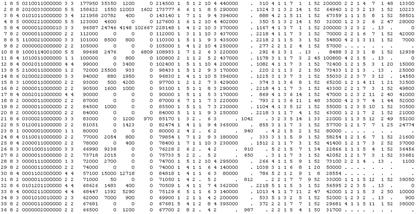
Рис. 2.1.3 Код отриманої вибірки
Отриманий код містить 36 стовбців, кожен з яких відповідає за окрему характеристику домогосподарства. Розшифровка коду наведена в додатку А.
Порівняння відборів
В своїй роботі я використовую другу конфігурацією StatVillage, а саме Mini Village, яка складається з 60-ти блоків. Для того, щоб порівняти точності систематичного, простого випадкового та стратифікованого відборів, я буду використовувати вибірки, добуті з 11-го та 13-го стовпців коду. Ці стовпці називаються TOTINCH та BUILTH, що є загальним доходом домогосподарства (включає в себе заробітну плату, пенсії, дівіденти та відсотки за депозитами і т.д.) та періодом побудови домогосподарства відповідно.
В результаті дослідження виявилось, що домогосподарства в StatVillage впорядковані за загальним доходом, а саме загальний дохід зменшується зі зростанням номеру домогосподарства. Логарифмічна регресія значуща. На рисунку 2.2.1 представлена діаграма розсіювання та логарифмічна регресія.
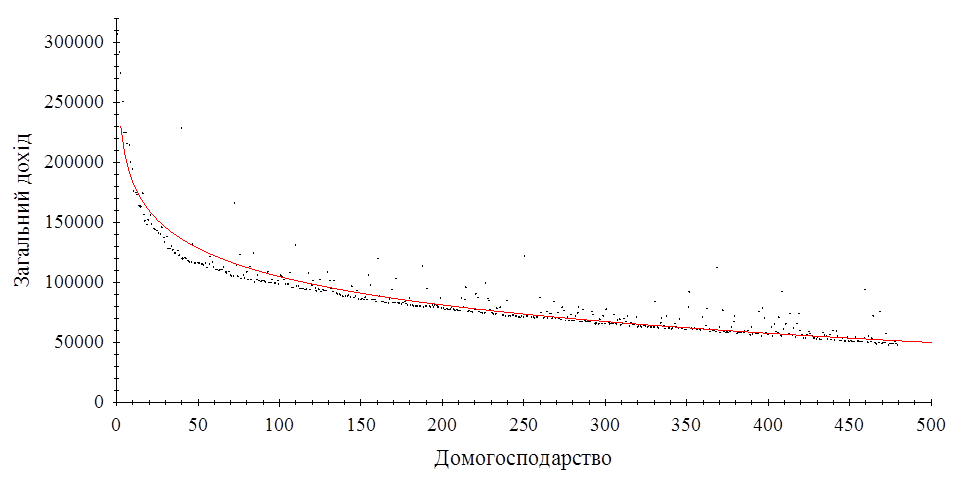Рис. 2.2.1 Діаграма розсіювання
Рівняння регресії: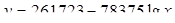 
F-статистика: 
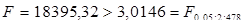Логарифмічна регресія значуща.
Порівняємо дисперсії середнього доходу домогосподарств при систематичному відборі кожного восьмого домогосподарства, простому випадковому відборі та стратифікованому відборі. Після отримання коду з 11-го стовпця (див. рис 2.1.3) запишемо дані в таблицю 2.2.1, розділивши на 60 страт.
Таблиця 2.2.1 Дані по 8-ми систематичним вибіркам
| Страта | Номер систематичної вибірки (k=8) |
| |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 214500 | 306000 | 291178 | 274200 | 250000 | 224230 | 224308 | 215448 | 249983 |
| 2 | 173777 | 200000 | 194322 | 175879 | 175000 | 173058 | 163673 | 162425 | 177266,8 |
| 3 | 143140 | 156667 | 150750 | 148433 | 151774 | 155215 | 147700 | 144781 | 149807,5 |
| 4 | 127600 | 142800 | 140900 | 140000 | 145148 | 137400 | 132998 | 137526 | 138046,5 |
| 5 | 228148 | 127706 | 129400 | 127109 | 124365 | 124324 | 126280 | 122300 | 138704 |
| 6 | 116200 | 120000 | 120393 | 120021 | 117561 | 116876 | 116400 | 131253 | 119838 |
| 7 | 112000 | 116000 | 116000 | 116000 | 115000 | 115400 | 114497 | 115936 | 115104,1 |
| 8 | 110300 | 114766 | 121294 | 117000 | 112100 | 110000 | 110000 | 109600 | 113132,5 |
| 9 | 105000 | 110830 | 112144 | 108481 | 108000 | 108601 | 105493 | 105000 | 107943,6 |
| 10 | 108953 | 165544 | 114427 | 105200 | 122916 | 102865 | 105664 | 102900 | 116058,6 |
| 11 | 100800 | 102400 | 113340 | 101800 | 124400 | 100702 | 102567 | 105400 | 106426,1 |
| 12 | 102400 | 100400 | 101300 | 101000 | 100333 | 108470 | 99070 | 99800 | 101596,6 |
| 13 | 98433 | 99400 | 98957 | 100871 | 98719 | 105833 | 104889 | 101700 | 101100,3 |
| 14 | 96830 | 98100 | 98000 | 107589 | 96050 | 96000 | 130797 | 96193 | 102444,9 |
| 15 | 97700 | 94728 | 94600 | 94542 | 93929 | 93728 | 107275 | 93933 | 96304,38 |
| 16 | 93100 | 100850 | 95029 | 93000 | 93626 | 101800 | 92312 | 93610 | 95415,88 |
| 17 | 90000 | 93082 | 108632 | 101221 | 94304 | 92100 | 101150 | 90800 | 96411,13 |
| 18 | 87000 | 90000 | 88846 | 88697 | 92593 | 88400 | 88000 | 88800 | 89042 |
| 19 | 85500 | 96348 | 87483 | 88615 | 92728 | 86028 | 86000 | 86257 | 88619,88 |
| 20 | 84000 | 87073 | 85320 | 105548 | 97503 | 85800 | 85691 | 85120 | 89506,88 |
| 21 | 85170 | 120000 | 87893 | 83514 | 84134 | 83201 | 83080 | 83000 | 88749 |
| 22 | 82474 | 93489 | 82720 | 82530 | 102614 | 82800 | 82986 | 82080 | 86461,63 |
| 23 | 80000 | 84000 | 81777 | 80539 | 86759 | 81200 | 80800 | 80000 | 81884,38 |
| 24 | 79854 | 80000 | 80400 | 80000 | 113400 | 79350 | 80050 | 94375 | 85928,63 |
| 25 | 78400 | 79000 | 81268 | 79400 | 80800 | 79800 | 79532 | 86117 | 80539,63 |
| 26 | 76228 | 78075 | 77600 | 77985 | 77650 | 77359 | 79122 | 77096 | 77639,38 |
| 27 | 75733 | 77000 | 76149 | 76000 | 86069 | 78974 | 85351 | 95990 | 81408,25 |
| 28 | 74700 | 76400 | 75853 | 75000 | 76983 | 90305 | 87022 | 75528 | 78973,88 |
| 29 | 74000 | 74946 | 74961 | 99015 | 86590 | 84569 | 77300 | 74800 | 80772,63 |
| 30 | 84818 | 73587 | 77909 | 75210 | 79193 | 72400 | 73000 | 72110 | 76028,38 |
| 31 | 71050 | 72093 | 72200 | 72800 | 72800 | 71856 | 72174 | 71238 | 72026,38 |
| 32 | 70509 | 71400 | 71000 | 121762 | 71647 | 71397 | 72458 | 70750 | 77615,38 |
| 33 | 75129 | 70000 | 70800 | 70400 | 87400 | 74915 | 70000 | 70800 | 73680,5 |
| 34 | 69900 | 69731 | 73282 | 73792 | 69470 | 83568 | 69833 | 74300 | 72984,5 |
| 35 | 67681 | 69105 | 79079 | 76779 | 68550 | 71178 | 68033 | 72400 | 71600,63 |
| 36 | 67700 | 68400 | 71570 | 74400 | 78843 | 67400 | 67000 | 77141 | 71556,75 |
| 37 | 65659 | 66703 | 67217 | 66800 | 75000 | 72439 | 65400 | 66132 | 68168,75 |
| 38 | 65000 | 69320 | 65000 | 71800 | 65000 | 76890 | 66154 | 65500 | 68083 |
| 39 | 69600 | 65300 | 73111 | 65065 | 68457 | 69200 | 64400 | 65229 | 67545,25 |
| 40 | 63000 | 67200 | 71943 | 63652 | 66020 | 64400 | 63993 | 70740 | 66368,5 |
| 41 | 62900 | 63800 | 63800 | 62893 | 63200 | 63200 | 62697 | 63306 | 63224,5 |
| 42 | 63519 | 62500 | 62763 | 83643 | 62400 | 62095 | 65900 | 69725 | 66568,13 |
| 43 | 62364 | 61611 | 71443 | 61304 | 61300 | 61200 | 61908 | 65000 | 63266,25 |
| 44 | 92240 | 61400 | 68700 | 61355 | 61623 | 60468 | 61151 | 79534 | 68308,88 |
| 45 | 71233 | 61612 | 60800 | 61800 | 62000 | 60800 | 60910 | 60000 | 62394,38 |
| 46 | 58988 | 60374 | 63684 | 78065 | 60733 | 59000 | 59400 | 59400 | 62455,5 |
| 47 | 58400 | 111951 | 62227 | 58224 | 76761 | 58975 | 58000 | 58450 | 67873,5 |
| 48 | 57800 | 58500 | 62910 | 66981 | 71500 | 57400 | 57600 | 57800 | 61311,38 |
| 49 | 58354 | 57800 | 58871 | 58544 | 60217 | 56358 | 62763 | 57060 | 58745,88 |
| 50 | 55900 | 56800 | 57467 | 75196 | 55479 | 78122 | 69699 | 57527 | 63273,75 |
| 51 | 55350 | 56685 | 62369 | 55000 | 65300 | 59148 | 58400 | 71000 | 60406,5 |
| 52 | 61671 | 91516 | 61052 | 65277 | 56550 | 56850 | 73512 | 56000 | 65303,5 |
| 53 | 56467 | 54000 | 65700 | 73998 | 59781 | 55788 | 53530 | 53000 | 59033 |
| 54 | 52191 | 58700 | 57219 | 55441 | 53533 | 53300 | 52163 | 53879 | 54553,25 |
| 55 | 59391 | 52621 | 58086 | 55800 | 55500 | 52475 | 55818 | 52335 | 55253,25 |
| 56 | 51000 | 51713 | 59277 | 55347 | 51333 | 51600 | 53465 | 51857 | 53199 |
| 57 | 50527 | 54560 | 51000 | 51857 | 50859 | 50800 | 54540 | 50700 | 51855,38 |
| 58 | 53475 | 50500 | 50460 | 53426 | 93669 | 50000 | 55000 | 50800 | 57166,25 |
| 59 | 49517 | 71853 | 49400 | 49000 | 49214 | 75349 | 48594 | 49582 | 55313,63 |
| 60 | 47900 | 57499 | 48000 | 48992 | 48360 | 48400 | 50649 | 49105 | 49863,13 |
| 83852,88 | 88407,3 | 86154,58 | 86896,53 | 87045,67 | 83855,98 | 83469,18 | 83002,8 | 5120137 |
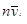
| 5031173 | 5304438 | 5169275 | 5213792 | 5222740 | 5031359 | 5008151 | 4980168 | |
У кожній страті міститься 1 блок, тобто 8 домогосподарств.
Знайдемо середнє та дисперсію для всієї популяції:
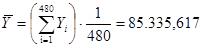
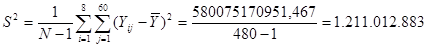
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
.
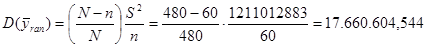Середнє значення систематичної вибірки має розподіл
~ 
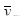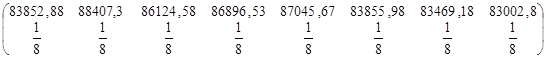
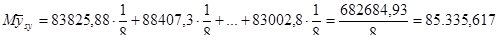
Оцінка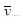 
є незміщеною оцінкою для 
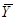, дійсно 
.
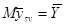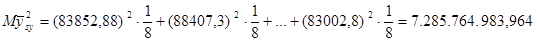
Дисперсія систематичної вибірки дорівнює
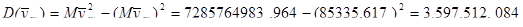
Тепер знайдемо дисперсію одиниць, що належать до однієї і тієї самої страти:
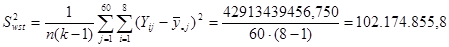
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
.
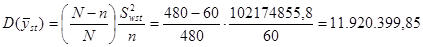Отже, ми отримали такі результати:
.
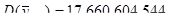
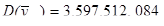
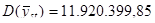Це означає, що
.
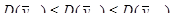При наявності логарифмічної залежності між загальним доходом та номером домогосподарства систематичний відбір виявився точнішим за простий випадковий та стратифікований відбори.
Тепер розглянемо дані, в яких відсутній тренд. Використовуємо вибірки, добуті з 13-го стовпця коду. Цей стовбець має назву BUILTH і відповідає за період побудови домогосподарства.
В результаті дослідження даної вибірки, виявилось, що залежність між періодом побудови та номером домогосподарства відсутня. Лінійна регресія не значуща. На рисунку 2.2.2 представлена діаграма розсіювання та відсутність лінійної регресії.
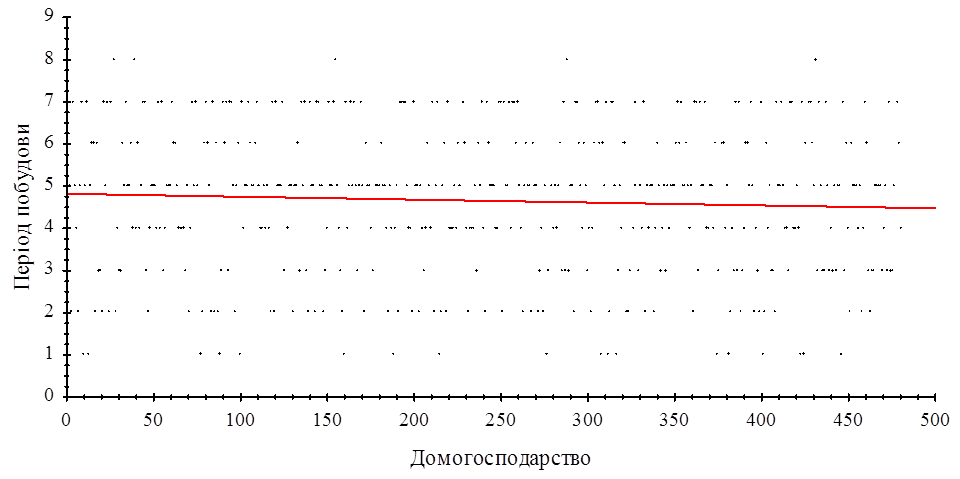Рис. 2.2.2 Діаграма розсіювання
Рівняння регресії: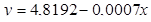 
F-статистика: 
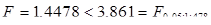Лінійна регресія не значуща
Порівняємо дисперсії середнього періоду побудови домогосподарства при систематичному відборі кожного восьмого домогосподарства, простому випадковому відборі та стратифікованому відборі. Після отримання коду з 13-го стовпця (див. рис 2.1.3) запишемо дані в таблицю 2.2.2, розділивши на 60 страт.
Таблиця 2.2.2 Дані по 8-ми систематичним вибіркам
| Страта | Номер систематичної вибірки (k=8) |
| |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 5 | 7 | 5 | 2 | 7 | 5 | 4 | 2 | 4,625 |
| 2 | 6 | 7 | 1 | 5 | 7 | 1 | 5 | 6 | 4,75 |
| 3 | 7 | 2 | 6 | 3 | 3 | 2 | 7 | 5 | 4,375 |
| 4 | 6 | 2 | 7 | 8 | 2 | 4 | 3 | 3 | 4,375 |
| 5 | 4 | 5 | 7 | 5 | 5 | 6 | 4 | 8 | 5,5 |
| 6 | 4 | 6 | 4 | 5 | 7 | 7 | 3 | 2 | 4,75 |
| 7 | 3 | 5 | 5 | 5 | 4 | 7 | 4 | 7 | 5 |
| 8 | 5 | 4 | 5 | 5 | 5 | 7 | 6 | 6 | 5,375 |
| 9 | 4 | 4 | 4 | 4 | 4 | 3 | 5 | 2 | 3,75 |
| 10 | 7 | 7 | 5 | 7 | 5 | 1 | 2 | 6 | 5 |
| 11 | 1 | 6 | 5 | 2 | 7 | 2 | 6 | 2 | 3,875 |
| 12 | 5 | 3 | 7 | 6 | 7 | 3 | 7 | 7 | 5,625 |
| 13 | 5 | 2 | 5 | 6 | 1 | 7 | 4 | 5 | 4,375 |
| 14 | 4 | 7 | 6 | 5 | 5 | 6 | 7 | 5 | 5,625 |
| 15 | 2 | 4 | 5 | 4 | 5 | 4 | 2 | 7 | 4,125 |
| 16 | 5 | 7 | 5 | 5 | 5 | 7 | 3 | 4 | 5,125 |
| 17 | 5 | 5 | 2 | 5 | 5 | 6 | 3 | 7 | 4,75 |
| 18 | 7 | 7 | 3 | 2 | 7 | 5 | 5 | 2 | 4,75 |
| 19 | 5 | 7 | 5 | 5 | 2 | 3 | 4 | 7 | 4,75 |
| 20 | 1 | 5 | 7 | 8 | 5 | 4 | 3 | 2 | 4,375 |
| 21 | 3 | 7 | 4 | 5 | 7 | 5 | 7 | 5 | 5,375 |
| 22 | 4 | 5 | 7 | 5 | 2 | 6 | 5 | 5 | 4,875 |
| 23 | 4 | 3 | 5 | 5 | 5 | 6 | 5 | 5 | 4,75 |
| 24 | 7 | 2 | 5 | 4 | 1 | 4 | 5 | 2 | 3,75 |
| 25 | 7 | 7 | 7 | 7 | 5 | 4 | 4 | 2 | 5,375 |
| 26 | 6 | 5 | 5 | 2 | 5 | 4 | 3 | 4 | 4,25 |
| 27 | 2 | 5 | 4 | 7 | 2 | 5 | 7 | 1 | 4,125 |
| 28 | 5 | 5 | 6 | 2 | 7 | 4 | 4 | 4 | 4,625 |
| 29 | 4 | 4 | 6 | 5 | 7 | 6 | 4 | 2 | 4,75 |
| 30 | 4 | 4 | 4 | 5 | 3 | 6 | 5 | 7 | 4,75 |
| 31 | 4 | 2 | 7 | 6 | 5 | 5 | 5 | 4 | 4,75 |
| 32 | 4 | 7 | 7 | 2 | 7 | 5 | 5 | 7 | 5,5 |
| 33 | 5 | 7 | 7 | 6 | 7 | 5 | 4 | 2 | 5,375 |
| 34 | 2 | 6 | 5 | 5 | 2 | 6 | 5 | 5 | 4,5 |
| 35 | 4 | 3 | 4 | 2 | 5 | 1 | 3 | 5 | 3,375 |
| 36 | 8 | 5 | 4 | 5 | 6 | 3 | 7 | 3 | 5,125 |
| 37 | 5 | 3 | 5 | 5 | 2 | 7 | 7 | 6 | 5 |
| 38 | 6 | 4 | 6 | 5 | 3 | 4 | 2 | 4 | 4,25 |
| 39 | 1 | 7 | 7 | 6 | 1 | 6 | 5 | 7 | 5 |
| 40 | 4 | 2 | 7 | 7 | 5 | 1 | 3 | 5 | 4,25 |
| 41 | 7 | 6 | 6 | 2 | 2 | 3 | 4 | 5 | 4,375 |
| 42 | 5 | 3 | 5 | 4 | 7 | 2 | 5 | 4 | 4,375 |
| 43 | 5 | 5 | 2 | 4 | 6 | 5 | 3 | 4 | 4,25 |
| 44 | 7 | 3 | 5 | 4 | 5 | 5 | 5 | 6 | 5 |
| 45 | 5 | 6 | 7 | 5 | 5 | 6 | 5 | 4 | 5,375 |
| 46 | 7 | 2 | 7 | 7 | 3 | 7 | 5 | 5 | 5,375 |
| 47 | 3 | 4 | 4 | 5 | 5 | 4 | 6 | 1 | 4 |
| 48 | 3 | 6 | 6 | 4 | 5 | 1 | 2 | 4 | 3,875 |
| 49 | 6 | 7 | 3 | 7 | 2 | 3 | 4 | 6 | 4,75 |
| 50 | 7 | 5 | 7 | 5 | 2 | 4 | 3 | 2 | 4,375 |
| 51 | 2 | 1 | 2 | 6 | 4 | 5 | 3 | 3 | 3,25 |
| 52 | 3 | 7 | 5 | 5 | 7 | 5 | 4 | 4 | 5 |
| 53 | 7 | 7 | 7 | 4 | 4 | 5 | 4 | 1 | 4,875 |
| 54 | 3 | 1 | 6 | 7 | 7 | 6 | 5 | 8 | 5,375 |
| 55 | 4 | 7 | 5 | 3 | 3 | 7 | 5 | 3 | 4,625 |
| 56 | 3 | 3 | 5 | 3 | 5 | 5 | 1 | 7 | 4 |
| 57 | 4 | 6 | 4 | 2 | 6 | 5 | 5 | 5 | 4,625 |
| 58 | 3 | 5 | 2 | 4 | 7 | 6 | 3 | 2 | 4 |
| 59 | 5 | 3 | 5 | 5 | 5 | 5 | 3 | 4 | 4,375 |
| 60 | 4 | 3 | 7 | 3 | 3 | 5 | 7 | 6 | 4,75 |
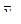
| 4,55 | 4,75 | 5,18 | 4,7 | 4,63 | 4,62 | 4,4 | 4,4 | 279,25 |
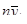
| 273 | 285 | 311 | 282 | 278 | 277 | 264 | 264 | |
Знайдемо середнє та дисперсію для всієї популяції:
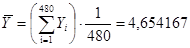
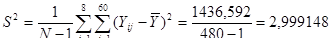
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
.
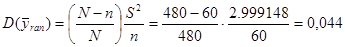Середнє значення систематичної вибірки має розподіл
~ 
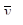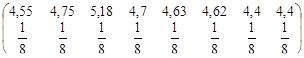
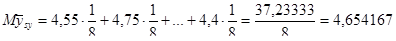
Також отримали, що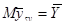 
.
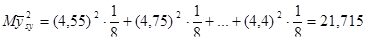
Дисперсія систематичної вибірки дорівнює
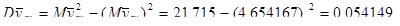
Тепер знайдемо дисперсію одиниць, що належать до однієї і тієї самої страти:
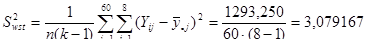
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
.
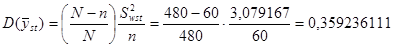Отже, ми отримали такі результати:
.
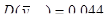
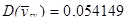
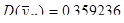Це означає, що
.
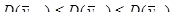При відсутності тренду систематичний відбір виявився ефективнішим ніж стратифікований відбір, але менш точним ніж простий випадковий відбір. Якщо порівняти дисперсії систематичної та простої випадкової вибірок, то виявиться що вони дуже мало відрізняються. При випадковому порядку розміщення одиниць систематичний відбір в середньому рівносильний простому випадковому відбору (останнє підтверджує теоретичні положення підрозділу 1.3).
Для підвищення точності систематичного відбору, при дослідженні періоду побудови домогосподарства, застосуємо стратифікований систематичний відбір. Основна його ідея розглядалась у підрозділі 1.9. Отже, всю популяцію, яка складається з 60-ти блоків (по 8 домогосподарств у кожному), ділимо на 2 страти. В першій страті розміщуються з 1-го по 32-й блоки (тобто 256 домогосподарств), а в другій – з 33-го по 60-й блоки (224 домогосподарства). З кожної страти здобуваємо систематичні вибірки кожної 8-ї одиниці. Всього комбінацій здобуття таких систематичних вибірок з двох страт – 64 (8 комбінацій з першої страти та 8 – з другої страти). Середнє значення стратифікованої систематичної вибірки рахується за формулою
,
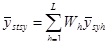де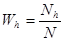 
- це вага страти 
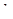, а 
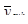- середнє значення систематичної вибірки у страті 
.
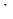Так як я буду розглядати 2 страти, то середнє значення стратифікованої систематичної вибірки має вигляд:
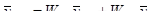
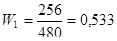
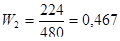
а для кожної систематичної вибірки у першій або другій страті своє.
Після розглядання всіх стратифікованих систематичних вибірок кожної 8-ї одиниці запишемо розподіл 
:
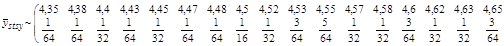
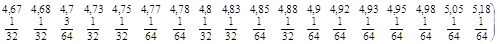
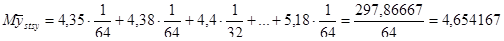
Також має місце рівність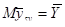 
.
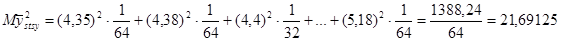
Дисперсія середнього стратифікованої систематичної вибірки дорівнює:
.
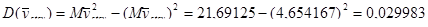При застосуванні стратифікованого систематичного відбору для періоду побудови домогосподарства маємо наступні результати:
.
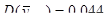
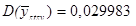
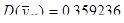Це означає, що
.
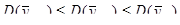При відсутності тренду стратифікований систематичний відбір є точнішим за простий випадковий та стратифікований відбори. Тобто стратифікований систематичний відбір дає більш точну оцінку ніж звичайний систематичний відбір.
Висновки
Вибірковий метод – метод дослідження, що дозволяє робити висновок про характер розподілу досліджуваних ознак популяції на основі розгляду деякої її частини (тобто вибірки). Прикладом вибіркових обстежень може бути визначення середнього рівня доходів населення, визначення переліку споживчих переваг, визначення рейтингу кандидата на виборах та інші. Існують різні методи вибіркового обстеження: простий випадковий відбір, стратифікований відбір, систематичний відбір, кластерний та інші. Для різних популяцій різні методи відбору можуть бути більш точними або менш точними.
Розглянемо простий, систематичний та стратифікований відбори. Простим випадковим відбором називається спосіб добування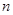 
одиниць вибірки з 
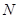одиниць популяції так, що кожна з 
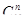вибірок має рівну імовірність бути відібраною. За допомогою таблиці або датчика випадкових чисел добуваємо вибірку обсягом .
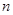Систематичний відбір полягає у тому, що з популяції, одиниці якої перенумеровані від 1 до 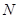, для здобуття вибірки обсягу 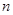спочатку навмання вибираємо будь-яку одиницю з перших 
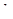одиниць популяції (наприклад, п’яту одиницю з 8-ми одиниць). Після вибору першої одиниці вибираємо кожну 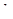-ту одиницю популяції (тобто 10-ту, 15-ту, 20-ту, 25-ту,…., 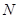-ту). Таку вибірку називають систематичною вибіркою кожної 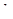-ї одиниці.
Стратифікований відбір полягає в тому, що вся популяція поділяється на менші під популяції (страти), які не мають спільних одиниць і кожна з яких внутрішньо однорідна. Потім за допомогою простого випадкового відбору з кожної страти здобувається вибірка. Такий відбір називається стратифікованим випадковим відбором. Наприклад, популяція з 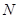одиниць поділена на 
страт, по 8 одиниць у кожній страті. З кожної страти здобуваємо по 2 одиниці за допомогою таблиці або датчика випадкових чисел. В результаті отримаємо: в першій страті числа 2, 7; в другій страті - 13, 16; і т.д.
В роботі ставиться задача порівняння точності систематичного відбору, простого випадкового та стратифікованого відбору.
Для розв’язання цієї задачі використано наступні теоретичні положення.
1. Середнє значення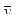 
систематичної вибірки є незміщеною оцінкою для середнього значення популяції .
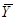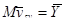(1)
2. Дисперсія середнього значення систематичної вибірки визначається формулою 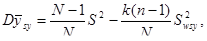(2)
(2)
де дисперсія одиниць, які належать одній систематичній вибірці визначається формулою 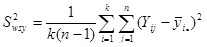(3),
(3)
а дисперсія популяції визначається формулою 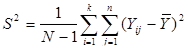(4)
(4)
3. Середнє значення для систематичної вибірки більш точне, ніж середнє для простої випадкової вибірки
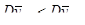
тоді і тільки тоді, коли справедлива нерівність 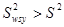(5)
. (5)
4. Дисперсія середнього значення систематичної вибірки може визначатись й формулою 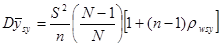(6)
, (6)
де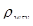 
- коефіцієнт кореляції між парами одиниць, що належать до однієї й тієї самої систематичної вибірки.
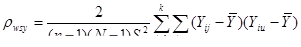(7)
5. Дисперсія середнього значення систематичної вибірки може ще визначатись формулою 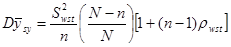(8)
, (8)
де дисперсія одиниць, що належать до однієї й тієї самої страти визначається формулою 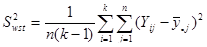(9)
. (9)
Величина
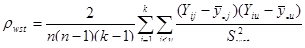. (10)
є коефіцієнтом кореляції між відхиленнями від середнього значення для страти по всім парам одиниць, що належать до однієї й тієї ж систематичної вибірки.
Зауважимо, що формули 2, 6, 8 - еквівалентні
6. Якщо в популяції одиниці розташовані навмання розглянемо всі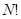 
скінчених популяцій, що утворюються за допомогою 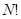перестановок деякого набору чисел 
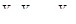. Тоді в середньому по всім цим скінченим популяціям справедлива формула (11)
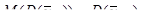. (11)
Тобто, коли одиниці вибірки розташовані випадково систематичний відбір в середньому рівносильний простому випадковому відбору.
Якщо між деякими характеристиками популяції наявна лінійна залежність, то справедлива нерівність (12).
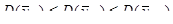. (12)
Тобто, стратифікований відбір точніший за систематичний відбір, який в свою чергу точніший простого випадкового відбору.
В своїй роботі я порівнювала точність систематичного відбору, простого випадкового та стратифікованого відбору, користуючись програмою StatVillage.
StatVillage – це гіпотетичне місто, яке складається з окремих домогосподарств і використовується як база даних для студентів та аспірантів, що вивчають вибіркові методи.
Дані домогосподарств для StatVillage обирались навмання з результатів перепису сімей, що мешкали у місті Ванкувері, Британській Колумбії, Канаді у 1991 році. Сам перепис населення проходив шляхом анонімного анкетування. Бралися до уваги наступні характеристики:
· демографічні показники (розмір домогосподарства та його склад за віком та статтю);
· показники доходу (зайнятість, інвестиції, валові витрати, різні доходи домогосподарств та інші);
· житлові характеристики (тип житла, рік побудови, своє житло чи орендоване, оціночна вартість, щомісячні витрати на розміщення та інші);
· характеристика двох членів сім’ї, які відповідають за добробут сім’ї (вік, стать, професія, рідна мова, освіта, зайнятість і т.д;)
Домогосподарства були розташовані згідно з загальним доходом від найбільшого до найменшого.
Існують три конфігурації міста StatVillage: Maximal village – складається зі 128 блоків, Mini village – складається з 60 блоків, та Micro village – складається з 36 блоків.
Для того, щоб отримати дані з міста StatVillage, необхідно спочатку відмітити домогосподарства позначкою. Після чого натискаючи кнопку «Get the sample units», отримуємо код. Отриманий код містить стовпці, кожен з яких відповідає за окрему характеристику домогосподарства
Порівнювати точності систематичного, простого та стратифікованого відборів, я буду використовувати вибірки, добуті з 11 та 13 стовпців коду. Ці стовпці відповідають – загальним доходам домогосподарства (включають в себе заробітну плату, пенсії, дівіденти та відсотки за депозитами) та періоду побудови домогосподарства.
В результаті дослідження виявилося, що загальний дохід зменшується зі зростанням номеру домогосподарства. Логарифмічна регресія значуща. Для загального доходу систематичний відбір виявився точнішим за простий випадковий та стратифікований відбори.
При дослідженні періоду побудови домогосподарства виявилося, що будь-яка залежність відсутня. Лінійна регресія не значуща. Систематичний відбір виявився більш точним ніж стратифікований випадковий відбір, але менш точним у порівнянні з простим випадковим відбором. Але можна помітити, що дисперсії простої випадкової та систематичної відбірок відрізняються мало. Отже, коли одиниці вибірки розташовані випадково систематичний відбір майже рівносильний простому випадковому відбору.
Останню оцінку можна покращити, застосувавши стратифікований систематичний відбір. Для цього всю популяцію ділимо на 2 страти. З кожної страти здобуваємо систематичні вибірки. Всього комбінацій здобуття вибірок з обох страт – 64. Дисперсія середнього стратифікованої систематичної вибірки виявилась меншою за відповідну дисперсію звичайної систематичної вибірки. Отже стратифікований систематичний відбір є точнішим за простий випадковий та стратифікований відбори.
Ефективність систематичного відбору в порівнянні зі стратифікованим або простим випадковим відбором суттєво залежить від особливостей популяції. Існують такі популяції, в яких систематичний відбір дає високу точність, але є й такі, для яких простий випадковий відбір є більш точним ніж систематичний. В будь-якому випадку для того, щоб застосування систематичного відбору було ефективним, необхідно знати будову популяції, з якої проводиться відбір.
Систематичні вибірки зручно намічати та вилучати. У більшості досліджень як по штучним, так і по реальним популяціям, вони вигравали в точності у порівнянні зі стратифікованими випадковими вибірками. Недоліки систематичної вибірки полягають в тому, що її точність може виявитись невисокою, якщо існує несподівана періодичність, і в тому, що невідомий надійний метод оцінювання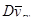 
за даними вибірки. Але не дивлячись на це, систематичний відбір рекомендований у наступних ситуаціях.
1. Якщо одиниці популяції розташовані в основному навмання або якщо стратифікування в популяції намічено досить слабо. В цьому випадку систематичний відбір застосовується, оскільки він зручний і не можна розраховувати на виграш в точності. Є вибіркові оцінки похибки, зміщення яких знаходиться у допустимих границях.
2. Якщо застосовується стратифікування з великим числом страт і систематична вибірка вилучається незалежно з кожній страти. В цьому випадку вплив прихованої періодичності має тенденцію нейтралізуватися і можна одержати оцінку похибки, яка заздалегідь перевищена. При іншому способі можна скористатися лише половиною страт та вилучити з кожної страти по дві систематичні вибірки з незалежним випадковим початком відліку. Такий спосіб забезпечує незміщену оцінку похибки.
3. При підвідборі одиниць. В цьому випадку виявляється, що у більшості практичних додатків можна отримати незміщену оцінку похибки вибірки.
4. При вибірковому вивчені популяцій з варіацією неперервного характеру за умови, що оцінка похибки вибірки звичайно не вимагається. Якщо проводиться ряд обстежень такого типу, то може виявитись достатнім перевіряти похибки вибірки лише від випадку до випадку. Йейтс (1948) вказує, що можна робити таку перевірку за допомогою додаткових спостережень.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Кокрен У. Методы выборочного исследования. Пер. с англ. И.М. Сонина. Под ред. А.Г. Волкова. – М.: Статистика, 1976. – 440 с. с ил.
2. Черняк О.І. Техніка вибіркових досліджень. – К.: МІВВЦ, 2001. – 248 с.
3. Пархоменко В.М. Методи вибіркових обстежень. Навчальний посібник. – К.,2001. – 148 с.
4. Govindarajulu Z. “Elements of sampling theory and methods”
5. Sharon L. Lohr Sampling: Design and Analysis – Duxbury Press, 1999. – 253c.
Дата: 2019-07-24, просмотров: 278.
