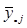Введемо поняття кластеру. Кластер – це група одиниць популяції, яка розглядається як вихідна одиниця вибірки. Нехай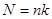 
. Популяцію можна розбити на 
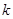кластерів, у кожному з яких знаходиться n одиниць. Тоді процедура випадкового відбору систематичної вибірки 
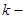го порядку така ж сама, як і процедура вибору одного із 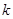кластерів (див. табл. 1.1.1).
Таблиця 1.1.1 Можливі систематичні вибірки 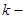го порядку
| Страти | Кластер | Середнє страти | |||||
| 1 | 2 | … | i | … | k | ||
| 1 |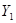 
| 
| … | 
| … | 
| 
|
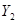
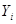
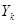
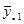
| 2 |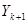 
| 
| … | 
| … | 
| 
|
| … | … | … | … | … | … | … | … |
| 
| 
| … | 
| … | 
| 
|
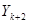
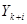
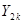
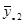
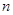
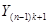
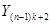
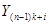
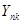
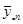
| Середнє систематичної вибірки |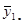 
| 
| … | 
| … | 
| |
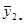
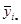
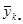
Нехай випадкова величина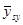 
– середнє значення систематичної вибірки, тобто 
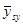з імовірністю 
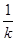дорівнює значенню , 
.
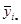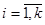Розподіл 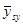має вигляд
~ 
.
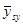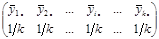Теорема 1.1.1. Середнє значення 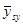систематичної вибірки є незміщеною оцінкою для середнього значення популяції 
.
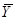Доведення.
,
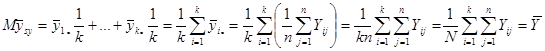де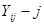 
-ий член 
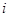-тої систематичної вибірки, 
, 
,
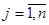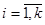зокрема, дисперсія 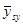дорівнює
.
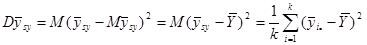Теорема доведена.
Теорема 1.1.2. Дисперсія середнього значення систематичної вибірки визначається формулою
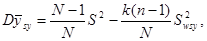(1.1.1)
Де
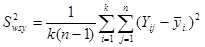
є дисперсією одиниць, які належать одній систематичній вибірці (wsy − від англ. within − всередині та systematic − систематичний).
Доведення.
Дисперсія популяції з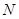 
одиниць визначається формулою
.
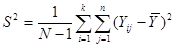Розглянемо тотожність
.
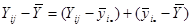Піднесемо обидві частини рівності до квадрату
.
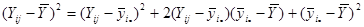Підсумуємо праву та ліву частини рівності за 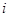та 
:
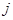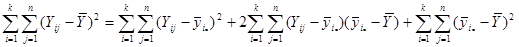
Покажемо, що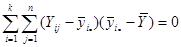 
:
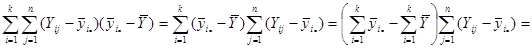
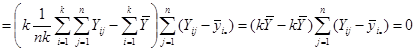
Отже, маємо
,
.
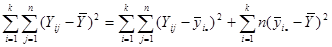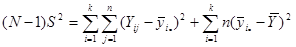Дисперсія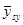 
дорівнює
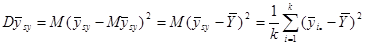
(обчислена за таблицею розподілу 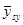). Тоді
.
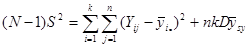Звідси
,
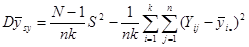або, що теж саме,
.
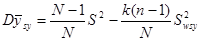Теорема доведена.
Наслідок. Середнє значення для систематичної вибірки більш точне, ніж середнє для простої випадкової вибірки, тобто
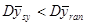
тоді і тільки тоді, коли
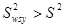. (1.1.2)
Доведення.
Дисперсія середнього значення простої випадкової вибірки дорівнює
.
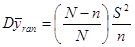Тоді з (1.1.1) випливає, що 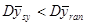тоді і тільки тоді, коли
.
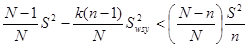Звідси маємо
.
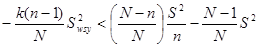Домножимо обидві частини нерівності на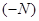 
та праворуч винесемо 
:
.
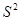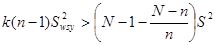Враховуючи, щ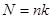о 
маємо
,
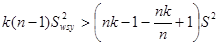або,
.
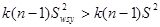Отже ,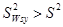 
.
Наслідок доведено.
Таким чином, систематичний відбір точніший, ніж простий випадковий відбір, якщо дисперсія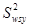 
одиниць систематичних вибірок більша дисперсії 
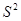всієї популяції. Систематичний відбір точний, коли одиниці всередині однієї й тієї ж вибірки неоднорідні, та неточний, коли вони однорідні. До цього можна прийти інтуїтивно. Якщо всередині систематичної вибірки варіація у порівнянні з варіацією популяції невелика, то послідовно вибрані одиниці вибірки несуть більш або менш однакову інформацію. Інший вираз для дисперсії наведемо у теоремі 1.1.3.
Теорема 1.1.3.
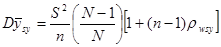, (1.1.3)
де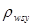 
- коефіцієнт кореляції між парами одиниць, що належать до однієї й тієї самої систематичної вибірки. Цей коефіцієнт визначається за формулою
,
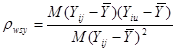де чисельник є середнім по всім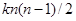 
різним парам, а знаменник – середнє по всім 
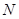значенням 
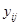. Розпишемо чисельник і знаменник:
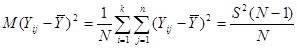
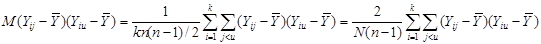
Підставивши отримані вирази у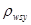 
отримаємо:
.
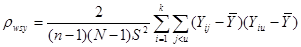Доведення.
Дисперсія середнього значення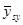 
систематичної вибірки дорівнює
.
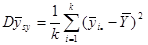Звідси маємо
.
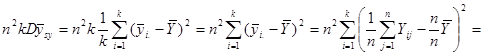
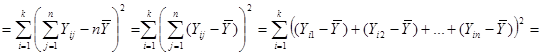
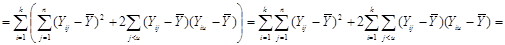
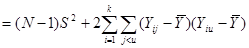Отже,
.
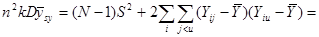
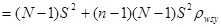Ділимо обидві частини на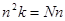 
і отримуємо вираз для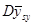 
.
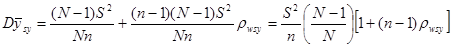
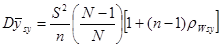Останній результат показує, що додатна кореляція між одиницями в одній і тій самій вибірці збільшує дисперсію вибіркового середнього. Навіть мала додатна кореляція може мати великий ефект за рахунок множника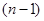 
.
Теорема доведена.
Дві попередні теореми виражали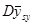 
через дисперсію популяції 
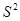, тобто співвідносили дисперсію 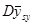з дисперсією для простої випадкової вибірки
.
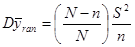Існує аналог теореми 1.1.3, в якому 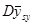виражена через дисперсію стратифікованої випадкової вибірки, де страти складалися з перших 
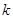одиниць, других 
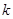одиниць і т.п. При позначеннях індекс 
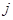при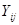 
відповідає номеру страти. Середнє для страти будемо записувати так 
.
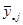Теорема 1.1.4.
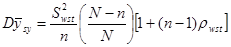, (1.1.4)
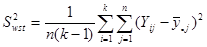
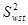– дисперсія одиниць, що належать до однієї й тієї самої страти. В знаменнику стоїть 
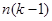, тому що кожна з 
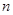страт вносить 
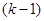ступінь вільності. Величина
.
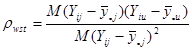є коефіцієнтом кореляції між відхиленнями від середнього значення для страти по всім парам одиниць, що належать до однієї й тієї ж систематичної вибірки.
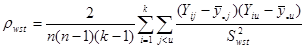. (1.1.5)
Доведення.
Доведення цієї теореми аналогічно доведенню теореми 1.1.3.
Дисперсія середнього значення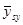 
систематичної вибірки дорівнює
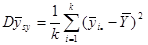
Розпишемо середнє значення популяції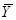 
через середнє стратифікованої вибірки :
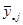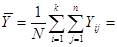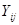{ - це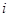 
-та одиниця 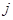-ї страти}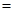 
.
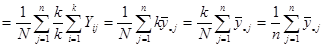Отже маємо
.
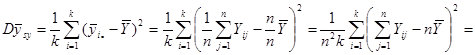
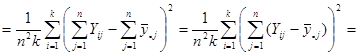
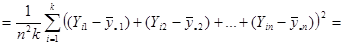
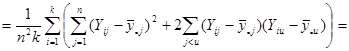
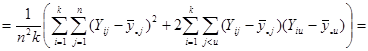
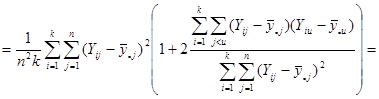
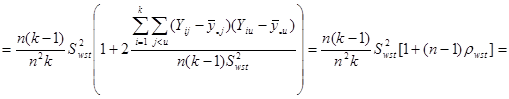
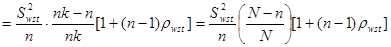Отже,
.
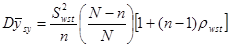Теорема доведена.
Наслідок. Якщо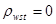 
, то систематична вибірка має ту саму точність, що й відповідна стратифікована випадкова вибірка з однією одиницею у кожній страті.
Це твердження випливає з того, що для такої стратифікованої випадкової вибірки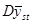 
дорівнює:
.
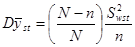Теорема 1.1.5. Дисперсія величини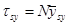 
, яка використовується для оцінювання сумарного значення популяції 
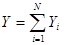, дорівнює
.
Приклад. У таблиці 1.1.2 наведені данні для невеликої штучної популяції, яка показує тенденцію до досить стійкого зростання значень ознаки у послідовності одиниць. Маємо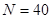 
, 
, 
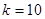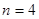. Кожний стовпчик відповідає деякій систематичній вибірці, а рядки є стратами. Приклад ілюструє ситуацію, коли кореляція «всередині страт» додатна. Наприклад, у першій вибірці кожне з чотирьох чисел (0, 6, 18, 26) менше середнього значення у страті, до якого воно належить. Це справедливо, з невеликим винятком, для перших п’яти систематичних вибірок. В останніх п’яти вибірках відхилення від середніх значень для страт в основному додатне. Таким чином, члени суми у виразі для 
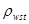переважно додатні. Відповідно до теореми 1.1.4 можна очікувати, що систематичний відбір буде менш точним, ніж стратифікований випадковий відбір з однією одиницею у кожній страті.
Таблиця 1.1.2 Данні по 10 систематичним вибіркам при обсязі вибірок 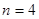та обсязі популяції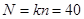 
| Страта | Номер систематичної вибірки ( |
| |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| I II III IV | 0 6 18 26 | 1 8 19 30 | 1 9 20 31 | 2 10 20 31 | 5 13 24 33 | 4 12 23 32 | 7 15 25 35 | 7 16 28 37 | 8 16 29 38 | 6 17 27 38 | 4,1 12,2 23,3 33,1 |
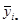
| 12, 5 | 14, 75 | 15, 25 | 15, 75 | 18, 75 | 17, 75 | 20, 5 | 22 | 22, 75 | 22 | 72,7 |
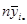
| 50 | 58 | 61 | 63 | 75 | 71 | 82 | 88 | 91 | 88 | |
Середнє значення систематичної вибірки має розподіл
~ 
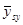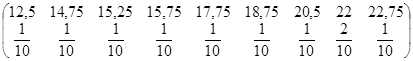
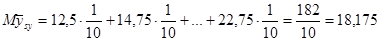
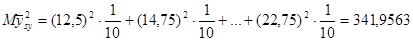
Дисперсія систематичної вибірки дорівнює
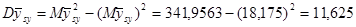
Знайдемо середнє та дисперсію для всієї популяції:
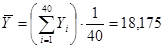
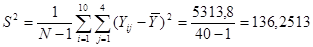
Тепер знайдемо дисперсію одиниць, що належать до однієї й тієї самої страти:
,
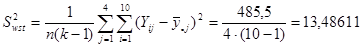де 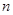- число страт, 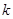- обсяг стратифікованої вибірки.
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
,
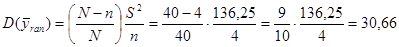де 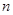- обсяг простої випадкової вибірки.
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
,
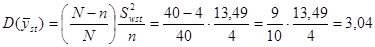де 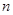- число страт.
Стратифікований випадковий відбір та систематичний відбір виявились набагато ефективнішими, ніж простий випадковий відбір, причому, як і очікувалось, систематичний відбір менш точний, ніж стратифікований випадковий відбір.
Дата: 2019-07-24, просмотров: 219.
