Систематичний відбір, оскільки він зручний, застосовується іноді до популяцій, в яких одиниці дійсно розташовані навмання. Наприклад, так буває при відборі з картотеки, що складена в алфавітному порядку за прізвищами, якщо змінюється ознака, яка ніяк не пов’язана з прізвищем того, кого обстежують. В цьому випадку не буде ніякої тенденції чи стратифікування по 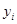 в розташуванні карток, ні кореляції між сусідніми одиницями.

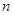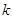У такій ситуації ми могли б очікувати, що систематичний відбір буде, по суті, рівносильний простому випадковому відбору та буде мати ту саму дисперсію. Для конкретної скінченої популяції при заданих значеннях  і  це не завжди вірно, тому що 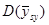, яка має  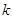ступенів вільності, при малих  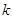досить нестійка і може виявитись як більше так і менше, ніж 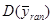. Але існують дві теореми, які показують, що в середньому ці дисперсії рівні.

Теорема 1.3.1. Розглянемо всі 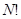 скінчених популяцій, що утворюються за допомогою  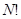перестановок деякого набору чисел 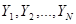. Тоді в середньому по всім цим скінченим популяціям

.

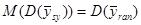Зауважимо, що 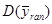 для усіх перестановок однакова.

Ця теорема стверджує, що якщо перестановку, яка визначає порядок значень у деякій конкретній скінченій популяції, можна вважати обраною навмання із можливих 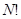 перестановок, то в середньому систематичний відбір еквівалентний простому випадковому відбору.

При іншому підході скінчену популяцію вважають добутою навмання з деякої нескінченої надпопуляції, що має певні властивості. Теорема 1.3.1 відноситься не до будь-якої скінченої популяції, а до середнього по всім скінченим популяціям, які можуть бути добуті із даної нескінченої надпопуляції.

Позначимо через 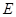- середнє по всім скінченним популяціям, які можуть бути добуті з даної надпопуляції.

Теорема 1.3.2. Якщо змінні 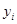 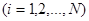добуті за допомогою випадкового відбору із надпопуляції, для якої

, ,

.

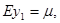
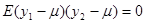
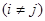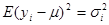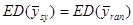Головну роль відіграють дві умови:

1) всі 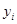 мають одне і теж середнє 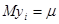, тобто в їх змінах відсутній будь-який тренд;

2) між значеннями 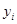 та 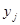 у двох різних точках відсутня лінійна кореляція. Дисперсія 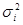може бути різною для різних .

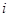Доведення. Для будь-якої визначеної скінченої популяції

.

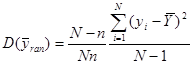Далі,

.

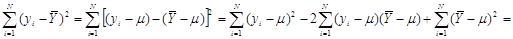
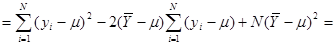
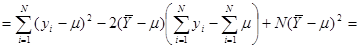
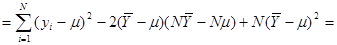
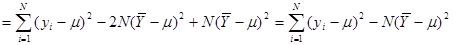Оскільки 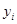 та 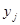 некорельовані 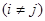, то

.

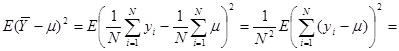
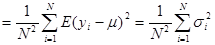Отже,

.

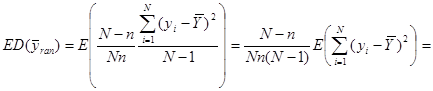
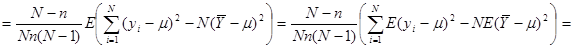
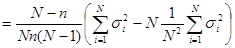Звідси

.

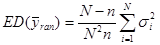Повертаючись до 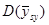 позначимо через  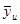середнє значення ознаки для 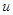-тої систематичної вибірки. Для будь-якої визначеної скінченої популяції

.

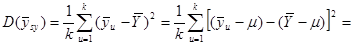
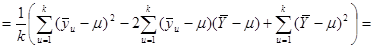
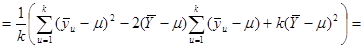
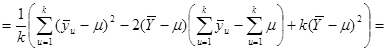
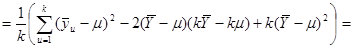
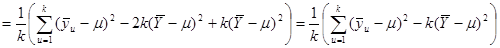За теоремою про дисперсію середнього для некорельованої вибірки, добутої з нескінченої популяції

~ ,

,

.

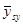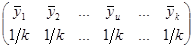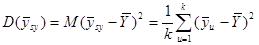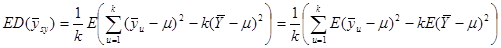Розглянемо докладніше вираз у дужках

.

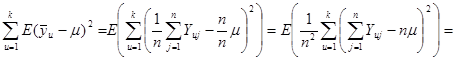
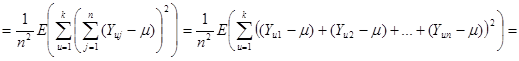
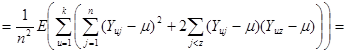
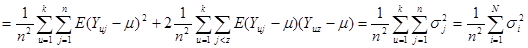Раніше було показано, що

.

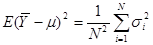Отже маємо

.

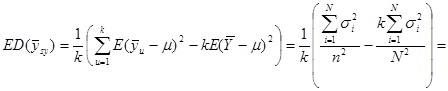
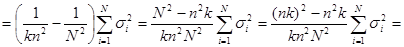
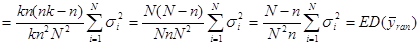Теорема доведена.