Динамика процентных ставок определяется взаимодействием целого ряда факторов: денежно-кредитной и налогово-бюджетной политики государства, состояния ликвидности банковской системы, тенденций развития инфляционных процессов, спроса на кредитные ресурсы со стороны реального сектора экономики, конъюнктуры смежных секторов финансового рынка и степени их интегрированности с сектором долговых финансовых инструментов, а также зависит от потока информационных сообщений, отражающих перспективы изменения состояния этих факторов, которые поступают рыночным агентам и определяют характер их последующих действий. Одни из факторов определяют долгосрочные тенденции изменения уровня процентных ставок, другие вызывают краткосрочные колебания, затухающие через несколько дней после первичной реакции рынка.
Автор полагает, что исследуя реакцию процентных ставок на изменения значений макроэкономических и финансовых показателей, отражающие перемены в состоянии экономики страны и конъюнктуре финансового рынка, можно построить модель прогнозирования, способную предсказывать направление движения процентных ставок более, чем в 50% случаев. Конечно, намерение добиться чрезвычайно высокой точности прогнозов является утопией. Набор доступных индикаторов, сколь бы широким он ни был, не может дать полностью адекватную картину комплекса сил, определяющих траекторию движения процентных ставок. Кроме того, эффективные рынки оперативно реагируют на вновь поступающую информацию, поэтому лаговые значения доступных индикаторов могут объяснить лишь часть вариации будущих изменений прогнозируемого показателя. В этой связи любая, даже самая эффективная модель прогнозирования обречена на ошибки; она не может гарантировать тесной корреляции между предсказанными и фактическими значениями объясняемой случайной переменной.
Однако попытка построить модель, верно определяющую направление движения рынка немногим более, чем в 50% случаев, и обеспечивающую небольшую положительную корреляцию между прогнозируемыми и фактическими изменениями, при определенных обстоятельствах может увенчаться успехом. По мнению автора, степень эффективности прогнозирования зависит от трех основных факторов: степени устойчивости тенденций, определявших динамику процентных ставок в недавнем прошлом, степени эффективности рынка, или скорости его адаптации к новым состояниям факторов среды, а также качества используемой модели. Два первых фактора находятся вне рамок контроля исследователя; они задают условия, в которых решается задача. Однако третий фактор поддается контролю: исследователь может выбирать различные концептуальные подходы к построению модели, вводить в рамки анализа или исключать из них различные переменные, сужать или расширять диапазон исторических данных, на основе которых оцениваются параметры модели.
В настоящей работе осуществляется проверка гипотезы о существовании сложной нелинейной зависимости между прошлыми значениями индикаторов российского финансового рынка и последующими изменениями спот-ставки рынка ГКО–ОФЗ для срока один год, отвечающей за часть вариации этих изменений. В качестве инструмента идентификации данной зависимости диссертантом используются нейронные сети – гибкие непараметрические модели, нашедшие широкое применение в различных финансовых приложениях.
Выбор нейронных сетей в качестве инструментального средства решения задачи прогнозирования динамики процентных ставок обусловлен их уникальной способностью к аппроксимации нелинейных зависимостей. Согласно следствию из теоремы Колмогорова–Арнольда, доказанному Хехт-Нильсеном, произвольная непрерывная функция нескольких переменных может быть аппроксимирована нейронной сетью с любой наперед заданной степенью точности.[80] Важным аргументом, послужившим основанием выбора нейронных сетей в качестве инструмента моделирования, стали успехи целого ряда исследователей в решении различных проблем анализа финансовых рынков на основе разработки нейросетевых приложений.
Обработка информации в нейронной сети осуществляется при помощи особых структурных элементов – искусственных нейронов. В нейрон поступает набор входных сигналов Xi. Каждый входной сигнал корректируется на соответствующий ему вес Wi. Потенциал нейрона рассчитывается по формуле
V = W0 + S Xi ´ Wi. (2.4.1)
Выходной сигнал нейрона формируется в результате преобразования потенциала нелинейной передаточной функцией f(V). Обычно для этого используется сигмоидальная функция вида
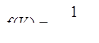. (2.4.2)
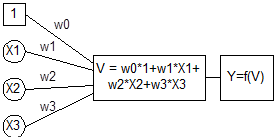
Рис.2.4.1. Математическая модель нейрона.
Объединяя искусственные нейроны в сети, можно получить различные варианты архитектуры. Но в финансовых приложениях чаще всего используются многослойные персептроны (multilayer perceptrons). Это нейронные сети, позволяющие моделировать зависимости между векторами входных и выходных переменных. В многослойных персептронах нейроны объединяются в слои, каждый из которых обрабатывает одинаковые входные сигналы.
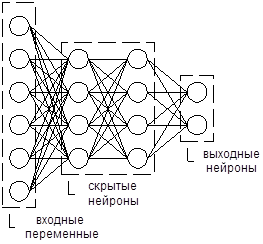
Рис.2.4.2. Архитектура многослойного персептрона.
Входной слой формируют независимые переменные, выходной – зависимые. Между ними располагаются скрытые слои. Выходы нейронов предыдущего слоя направляются на вход нейронов последующего слоя. База знаний нейронной сети представляет собой матрицу весов связей между нейронами.
Процесс настройки весов многослойного персептрона называется обучением. Для этого используется обучающая выборка – множество векторов значений объясняющих и объясняемых переменных. Цель обучения заключается в минимизации ошибки оценки объясняемых переменных на основе информации о значениях объясняющих переменных.
Итеративный алгоритм обучения многослойных персептронов, ставший впоследствии классическим и получивший название алгоритма обратного распространения ошибки (error backpropagation), впервые был разработан Полом Вербосом в 1974 г. в рамках работы над магистерской диссертацией в Гарвардском университете[81]. Однако работа Вербоса не была должным образом оценена и долгое время оставалась неизвестной крупнейшим ученым. В 1986 г. алгоритм обратного распространения был заново открыт и популяризирован Д.Румельхартом, Г.Хинтоном и Р.Вильямсом[82]. С начала 1990-х гг. алгоритм обратного распространения стал активно применяться в прикладных разработках.
Алгоритм обратного распространения осуществляет минимизацию функции ошибки, определенной на множестве возможных значений весов сети. Функция ошибки обычно задается как
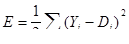, (2.4.3)
где 1/2 – константа, введенная для удобства при вычислении производных, i – порядковый номер выходного нейрона, Y – размер сигнала выходного нейрона, D – обучающее значение объясняемой переменной.
На каждой итерации работы алгоритма осуществляется переход к новой точке пространства весов сети. Для этого используется метод градиентного спуска, позволяющий выбрать направление, в котором скорость уменьшения значения функции ошибки является максимальной. Коррекция весов производится по правилу
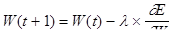, (2.4.4)
где E – функция ошибки, W – вес, l – коэффициент обучения (размер шага корректировки), t – порядковый номер итерации.
Вычисление производных функции ошибки по весам сети осуществляется по формуле
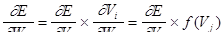, (2.4.5)
где j – номер нейрона предыдущего слоя, i – номер нейрона последующего слоя, W – вес, V – потенциал, f – передаточная функция.
Производные ошибки по потенциалам вычисляются по правилу цепи, которое и обеспечивает процесс обратного распространения ошибки из нейронов выходного слоя в нейроны предыдущих слоев.
Для выходных нейронов
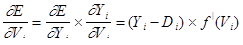. (2.4.6)
Для скрытых нейронов
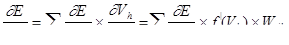, (2.4.7)
где h – номер нейрона последующего слоя, i – номер нейрона обрабатываемого слоя.
В целях ускорения процесса обучения часто используется модификация алгоритма обратного распространения, которая обеспечивает большую стабильность процесса корректировки за счет применения оператора экспоненциального сглаживания. В этом случае уравнение обучения принимает вид
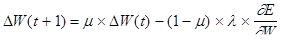, (2.4.8)
где m – момент, l – коэффициент обучения.
В ходе обучения сети многократно предъявляется один и тот же набор обучающих примеров. Чем дольше продолжается процесс обучения, тем лучше качество аппроксимации, демонстрируемое сетью при оценке значений выходных переменных по обучающей выборке. Однако через определенное число эпох обучения (под эпохой понимается однократное предъявление сети используемого набора обучающих примеров) улучшение качества аппроксимации начинает обеспечиваться не в результате правильной идентификации нелинейной зависимости между объясняющими и объясняемыми переменными, а за счет точности настройки на специфические особенности обучающих примеров. Этот феномен, получивший название переобучения (overtraining), находит отражение в падении способности сети к обобщению, то есть к адекватной оценке значений выходных переменных по наблюдениям, не предъявленным в ходе обучения.
Для того, чтобы разрешить проблему переобучения, массив исходных данных разбивается на обучающую и тестовую выборки. Обучающая выборка используется в процессе работы алгоритма коррекции матрицы весов сети. Тестовая выборка используется для контроля состояния обученности сети. Процесс обучения прекращается, когда значение ошибки оценки значений выходных переменных по тестовой выборке достигает минимума.
В первой половине 1990-х годов целый ряд исследователей обратился к методологии нейронных сетей как к инструментальному средству анализа финансовых рынков. Однако основные усилия обошли стороной сферу изучения процессов функционирования рынков облигаций. Большинство работ, опубликованных в этот период, посвящены прогнозированию динамики рынков акций и иностранных валют, определению рейтингов кредитоспособности заемщиков, оценке опционов.[83]
Первая попытка разработки нейросетевой модели прогнозирования конъюнктуры рынка облигаций была предпринята В.Ченгом, Л.Вагнером и Ч.Лином[84]. Их усилия были направлены на построение модели, прогнозирующей направление изменения цены тридцатилетней облигации Казначейства США через одну неделю. Используя в качестве объясняющих переменных спот-ставки для различных сроков вложений, индексы рынка акций, денежный агрегат M2, курсы доллара к японской иене и немецкой марке, а также цены на нефть и золото, они сконструировали нейронную сеть, оказавшуюся способной правильно определять направление изменения цены в 67% случаев.
Результаты, полученные Ченгом, Вагнером и Лином, показали, что задача краткосрочного прогнозирования конъюнктуры стабильного высоколиквидного рынка государственных облигаций с использованием нейросетевых моделей вполне разрешима. Однако российский рынок государственных ценных бумаг существенно отличен от американского, что ставит под сомнение возможность эффективного применения нейросетевых алгоритмов в целях поддержки принятия решений по управлению портфелем ГКО–ОФЗ.
Во-первых, очень сильное влияние на конъюнктуру рынка ГКО–ОФЗ оказывают политические события, которые практически не поддаются формализованному анализу и прогнозированию. Во-вторых, уровень ликвидности инструментов рынка ГКО-ОФЗ и объем совершаемых на нем операций крайне низок. По некоторым инструментам в течение торговой сессии вообще не заключается ни одной сделки, что совершенно нетипично для развитых рынков государственных ценных бумаг. В результате цены облигаций оказываются чувствительными к непредсказуемым колебаниям спроса и предложения со стороны отдельных операторов. В-третьих, макроэкономическое положение России характеризуется частыми и существенными изменениями, что не позволяет использовать в ходе анализа достаточно продолжительные исторические выборки.
В то же время все вышеизложенное позволяет предположить, что российский рынок ГКО–ОФЗ не является эффективным. Вполне возможно, что сигналы со смежных секторов финансового рынка отражаются на ценах государственных облигаций с небольшим лагом. Если эта гипотеза соответствует действительности, модель прогнозирования краткосрочных колебаний процентных ставок может оказаться способной обеспечить правильное определение направления движения рынка более, чем в 50% случаев. Изучение кросс-корреляций между темпом прироста спот-ставки рынка ГКО–ОФЗ для срока один год за одну неделю и темпами прироста некоторых индикаторов российского финансового рынка, оцененных по данным за период с 1 июня по 27 декабря 2000 г., позволило получить ряд свидетельств в пользу сделанного предположения.
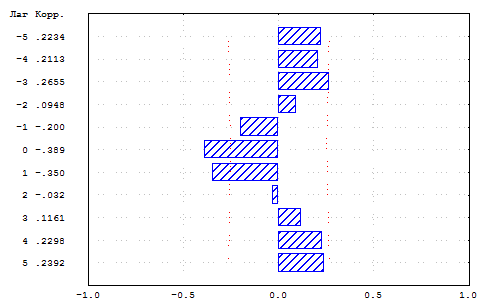
Рис.2.4.3. Кросс-корреляция между недельным темпом прироста спот-ставки рынка ГКО–ОФЗ для срока один год и недельным темпом прироста денежных остатков на корреспондентских счетах коммерческих банков в Банке России.
Рис.2.4.3 показывает, что темп прироста денежных остатков на корреспондентских счетах коммерческих банков в Банке России является опережающим индикатором для темпа прироста спот-ставки рынка ГКО–ОФЗ для срока один год. Коэффициенты корреляции для лагов в 0 и 1 неделю отрицательны и статистически значимы на 5% уровне. Повышение уровня ликвидности банковской системы сопровождается ростом спроса на государственные облигации, который приводит к снижению процентных ставок на рынке ГКО–ОФЗ. Уменьшение уровня ликвидности банковской системы вынуждает банки производить сокращение своих портфелей государственных облигаций, что влечет рост предложения на рынке и повышение уровня процентных ставок.
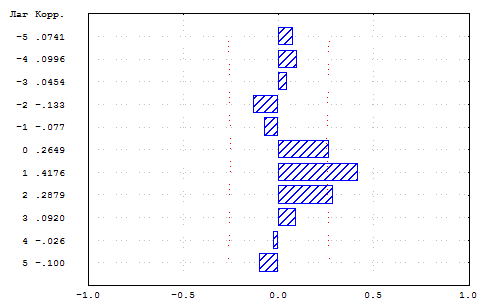
Рис.2.4.4. Кросс-корреляция между недельным темпом прироста спот-ставки рынка ГКО–ОФЗ для срока один год и недельным темпом прироста курса доллара США к российскому рублю.
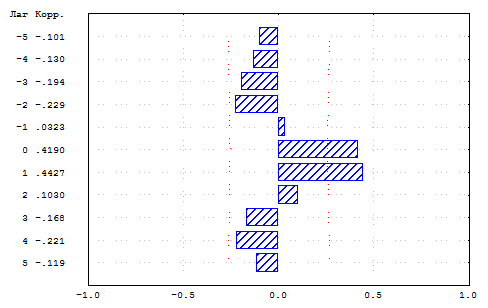
Рис.2.4.5. Кросс-корреляция между недельным темпом прироста спот-ставки рынка ГКО–ОФЗ для срока один год и недельным темпом прироста средневзвешенной процентной ставки по краткосрочным межбанковским кредитам (индикатора MIACR ).
Рис.2.4.4 показывает, что темп прироста курса доллара США также служит опережающим индикатором. Коэффициенты корреляции между темпом прироста спот-ставки рынка ГКО–ОФЗ для срока один год и этим показателем отрицательны и статистически значимы для задержек в 0, 1 и 2 недели. Ускорение темпов обесценения рубля влечет переток средств на валютный рынок, усиливает инфляционные ожидания и понижает цены рублевых облигаций. Укрепление рубля делает валютные операции непривлекательными и стимулирует спрос на государственные облигации, что вызывает падение процентных ставок.
Рис.2.4.5 демонстрирует тесную связь между рынком ГКО–ОФЗ и рынком межбанковских кредитов. Дефицит ресурсов на межбанковском кредитном рынке преодолевается за счет продажи части портфелей ГКО–ОФЗ; избыток ресурсов межбанковского кредитного рынка направляется на другие сегменты финансового рынка, в том числе на рынок государственных облигаций. Поэтому между процентными ставками рынков межбанковских кредитов и ГКО–ОФЗ наблюдается положительная корреляция, причем темп прироста ставки MIACR (средневзвешенной ставки по фактически предоставленным межбанковским кредитам) может использоваться для прогнозирования направления изменения ставок на рынке ГКО–ОФЗ через одну неделю.
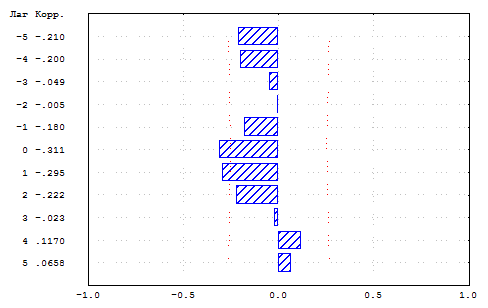
Рис.2.4.6. Кросс-корреляция между недельным темпом прироста спот-ставки рынка ГКО–ОФЗ для срока один год и недельным темпом прироста индекса РТС.
Рис.2.4.6 свидетельствует, что между темпом прироста капитализации рынка акций и процентными ставками на рынке ГКО–ОФЗ наблюдается статистически значимая отрицательная корреляция. Улучшение конъюнктуры рынка акций, вызванное позитивными сдвигами в ожиданиях инвесторов по поводу перспектив изменения макроэкономического положения страны, сопровождается снижением уровня процентных ставок. Ускорение падения цен на рынке акций может выступать фактором падения цен и на рынке ГКО–ОФЗ.
Анализ кросс-корреляционных функций показывает, что последующие изменения процентных ставок рынка ГКО–ОФЗ тесно связаны лишь с самыми последними изменениями на других сегментах российского финансового рынка. Поэтому при выборе объясняющих переменных модели прогнозирования целесообразно ограничиться несколькими последними значениями потенциальных опережающих индикаторов.
Между значениями различных объясняющих переменных может существовать тесная корреляционная зависимость, что делает использование некоторых из них в рамках модели прогнозирования нецелесообразным в связи с эффектом мультиколлинеарности. Для того, чтобы отобрать наиболее значимые опережающие индикаторы для модели прогнозирования темпа прироста спот-ставки рынка ГКО–ОФЗ для срока один год, диссертант воспользовался методом пошагового регрессионного анализа с последовательным включением наиболее значимых объясняющих переменных. В первоначальный набор объясняющих переменных были включены недельные темпы прироста пяти различных индикаторов: спот-ставки рынка ГКО–ОФЗ для срока один год, денежных остатков на корреспондентских счетах коммерческих банков в Банке России, обменного курса доллара США к российскому рублю, средневзвешенной ставки по фактически предоставленным краткосрочным межбанковским кредитам и индекса Российской торговой системы, взятые с задержками в 1, 2 и 3 недели относительно прогнозируемого показателя. В результате было получено следующее уравнение регрессии:
Rt= –0.0169 + 0.1957 Rt-1 – 0.0779 Bt-1 + 2.9992 Dt-1 + 1.8582 Dt-2 + 0.0270 Ct-1 – 0.2141 St-1 – 0.1351St-2 ,
(t) (-3.0121) (1.7080) (-1.2154) (1.8511) (1.1442) (2.1570) (-2.5473) (-1.7412)
где Rt – темп прироста спот-ставки рынка ГКО–ОФЗ для срока один год за неделю t, Bt – темп прироста остатков на корреспондентских счетах коммерческих банков в Банке России за неделю t, Dt – темп прироста обменного курса доллара США к российскому рублю за неделю t, Сt – темп прироста ставки MIACR за неделю t, St – темп прироста индекса РТС за неделю t.
В полученное уравнение регрессии вошли 7 объясняющих переменных, коэффициент детерминации R2 составил 0.4399. Таким образом, значительная часть последующих изменений процентных ставок рынка ГКО–ОФЗ получила объяснение при помощи модели множественной регрессии.
Однако в действительности характер зависимости между опережающими индикаторами и прогнозируемым показателем может являться нелинейным. Тогда использование нейронной сети вместо множественной регрессии позволяет существенно повысить качество модели. В этой связи автором было произведено обучение трехслойного персептрона с семью нейронами во входном слое (соответствующих семи объясняющим переменным регрессионной модели), четырьмя нейронами в единственном скрытом слое и одним нейроном в выходном слое (соответствующим прогнозируемому показателю).
Массив исходных данных за период с 1 июня по 27 декабря 2000 г., включающий значения переменных по состоянию на вторник и пятницу каждой недели, был разбит на обучающую и тестовую выборки. В состав обучающей выборки были включены 48 наблюдений, в состав тестовой выборки – 12 наблюдений (20% от их общего количества).
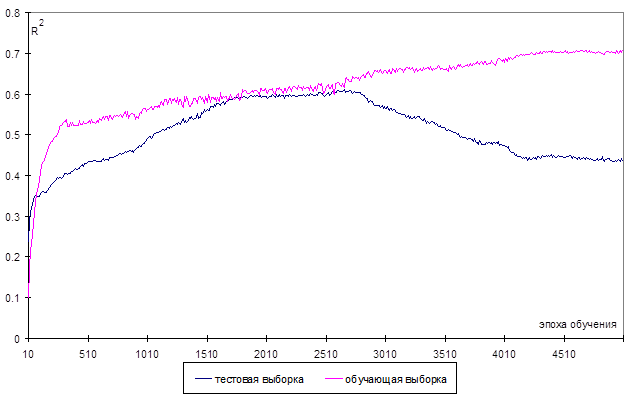
Рис.2.4.7. Кривая обучения нейросетевой модели прогнозирования недельного темпа прироста спот-ставки рынка ГКО–ОФЗ для срока один год.
В течение примерно 2500 эпох обучения коэффициент детерминации между фактическими и спрогнозированными изменениями процентной ставки повышался как по обучающей, так и по тестовой выборке, достигнув соответственно отметок 0.6033 и 0.5950. В последующем коэффициент детерминации по обучающей выборке продолжил увеличиваться, а коэффициент детерминации по тестовой выборке начал снижаться. Таким образом, оптимальное состояние обученности сети было достигнуто после 2500 эпох обучения. При этом были выявлены нелинейные зависимости между опережающими индикаторами и прогнозируемой переменной, что позволило автору добиться повышения коэффициента детерминации примерно на 36.5% по сравнению с линейной регрессионной моделью.
Для изучения характера влияния опережающих индикаторов на прогноз нейронной сети были построены профили чувствительности выходной переменной к изменению значения свободной входной переменной. При построении профилей чувствительности значения несвободных входных переменных фиксировались на уровне средних по выборке. Значения единственной свободной переменной варьировались в диапазоне (-2s; 2s), где s – среднеквадратическое отклонение ее выборочного распределения.
Рис.2.4.8. Профили чувствительности выходной переменной к изменению значений входных переменных.
Анализ профилей чувствительности показывает, что зависимости между лаговым значением темпа прироста процентной ставки, а также темпами прироста курса доллара и прогнозируемым показателем являются нелинейными. Небольшие колебания курса доллара практически не отражаются на последующих изменениях процентных ставок, в то время как в случае резких скачков обменного курса влияние валютного рынка на рынок государственных облигаций резко возрастает. Чувствительность прогнозируемой переменной к последним изменениям на рынках акций и иностранных валют выше по сравнению с ее чувствительностью к предшествующим изменениям. Направления воздействия опережающих индикаторов на прогнозируемую переменную соответствуют оценкам, полученным при рассмотрении кросс-корреляционных функций и построении линейной регрессионной модели.
Эффективность применения нейронной сети для краткосрочного прогнозирования конъюнктуры рынка ГКО–ОФЗ оценивалась автором путем сравнения предсказаний, сделанных обученной сетью каждую среду в течение периода с начала января по конец марта 2001 г., с фактическими изменениями процентной ставки, а также с прогнозами линейной регрессионной модели.
Ra – фактический темп прироста спот-ставки, Rp – прогноз темпа прироста спот-ставки
Рис.2.4.9. Результаты прогнозирования недельного темпа прироста спот-ставки
рынка ГКО–ОФЗ для срока один год в январе–марте 2001 г.
И нейронная сеть, и множественная регрессия смогли обеспечить положительное значение коэффициента корреляции между предсказанными и фактическими изменениями, но точность прогнозирования с использованием нейронной сети оказалась более высокой. Регрессионная модель верно определила направление изменения процентной ставки в семи случаях из двенадцати, в то время как нейронная сеть – в восьми случаях из двенадцати. Коэффициент корреляции между спрогнозированными и фактическими изменениями составил 0.3613 для регрессионной модели и 0.4268 для нейронной сети.
Значения коэффициентов детерминации существенно упали по сравнению с периодом, использованным для настройки параметров моделей (с 0.4399 до 0.1306 для линейной регрессии и с 0.5950 до 0.1822 для нейронной сети). Этот результат вполне объясним. Во-первых, механизм реагирования операторов рынка государственных облигаций на события, происходящие на других сегментах финансового рынка, претерпевает изменения с течением времени. Во-вторых, большое влияние на колебания процентных ставок оказывают факторы, не учитываемые в рамках модели прогнозирования и действующие различным образом в течение периодов настройки параметров модели и построения прогнозов.
В то же время обе построенные модели смогли превзойти по эффективности наивную модель отсутствия изменений. Нейронная сеть справилась с задачей определения направления движения процентных ставок в 67% случаев, то есть обеспечила такую же точность оценок, как и модель Ченга–Вагнера–Лина для американского рынка. Используя поступающую информацию о траектории движения процентной ставки, конъюнктуре смежных секторов финансового рынка и состоянии ликвидности банковской системы, удалось объяснить более 18% вариации последующих изменений спот-ставки рынка ГКО–ОФЗ для срока один год.
Полученные результаты позволяют заключить, что на рынке ГКО–ОФЗ нейросетевые модели прогнозирования обладают реальной предсказательной силой. Однако их использование в качестве одного из инструментов поддержки принятия решений можно рекомендовать лишь наиболее агрессивным инвесторам, характеризующимся высокой склонностью к риску и осуществляющим частый пересмотр структуры управляемого портфеля государственных облигаций.
Дата: 2019-07-24, просмотров: 247.
