Процентный риск владельца портфеля облигаций существенно зависит от того, в какой мере используемая модель управления соответствует реальным процессам, протекающим на конкретном рынке. Поэтому автор предлагает выделять такие составляющие процентного риска, как управляемый риск и остаточный риск. Управляемый процентный риск обусловлен такими сдвигами временной структуры процентных ставок, которые учитываются в рамках модели управления и используются при выводе рекомендаций по формированию структуры портфеля. Остаточный процентный риск обусловлен такими сдвигами временной структуры процентных ставок, которые не учитываются в рамках используемой модели управления, но наблюдаются в условиях данного рынка.

Инвесторы, осуществляющие операции на рынке ГКО–ОФЗ, испытывают объективную потребность в модели поддержки принятия решений, позволяющей обеспечить максимально полное устранение остаточного процентного риска. В этой связи диссертантом была поставлена и решена задача разработки модели иммунизации от непараллельных сдвигов временной структуры процентных ставок, адаптированной к условиям рынка ГКО–ОФЗ.

Максимизация зоны управляемого риска при иммунизации портфеля ГКО–ОФЗ определяет необходимость использования гибкой модели допустимых перемещений временной структуры процентных ставок. Такая модель должна включать непараллельные сдвиги, а также предоставлять возможность быстрой перенастройки параметров по мере поступления новой информации. По мнению диссертанта, эти условия выполняются в случае использования модели метода главных компонент

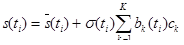,                                                                                     (2.1.1)

где s(t_i) – спот-ставка для срока вложений t_i, 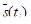 – среднее значение спот-ставки для срока вложений t_i, s(t_i) – среднеквадратическое отклонение cпот-ставки s(t_i), c_k – главная компонента временной структуры процентных ставок c порядковым номером k, K ­– число используемых главных компонент временной структуры процентных ставок, b_k(t_i) – коэффициент чувствительности спот-ставки s(t_i) к изменению значения главной компоненты временной структуры процентных ставок c_k (нагрузка по главной компоненте c_k).

Используя уравнение (2.1.1), можно выразить форвардные ставки через главные компоненты временной структуры спот-ставок. Действительно,

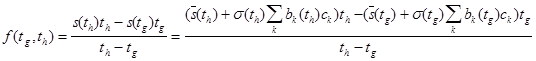,  (2.1.2)

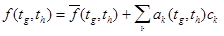,                                                                           (2.1.3)

где

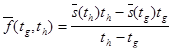,                                                                                        (2.1.4)

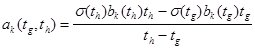.                                                                   (2.1.5)

В момент формирования портфеля состояние рынка описывается временной структурой процентных ставок s(t_i). Распространение среди операторов новой значимой информации (в частности, сообщений о неожиданных изменениях значений макроэкономических показателей или новых политических инициативах) ведет к изменению цен облигаций и временной структуры процентных ставок. После того, как рынок обработает поступившие сигналы, его состояние будет описываться новой временной структурой спот-ставок s*(t_i), которой соответствуют новые значения главных компонент 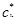 и форвардных ставок f*(t_g,t_h), причем

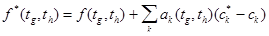.                                                                (2.1.6)

В результате рыночная стоимость портфеля через период времени m окажется равной

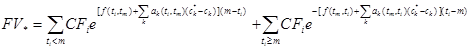.             (2.1.7)

Доходность портфеля за период времени m иммунизирована от колебаний главной компоненты временной структуры процентных ставок c_k, если изменение значения этой компоненты в начальный момент времени не может привести к падению доходности вложений ниже уровня s(m). Поэтому стоимость иммунизированного портфеля через период m не может упасть ниже уровня, определяемого начальной временной структурой форвардных ставок f(t_g,t_h). Отсюда для любого портфеля, иммунизированного от неблагоприятных изменений главной компоненты временной структуры процентных ставок c_k, должно выполняться неравенство

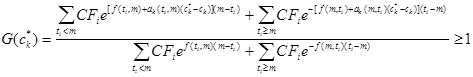.             (2.1.8)

При 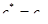 это неравенство выполняется для любого сформированного портфеля, т.к. G(c_k)=1. Поэтому оно выполняется и на всей области определения функции 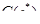, если в точке  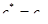достигается глобальный минимум данной функции. Для этого достаточно выполнения условий иммунизации первого и второго порядка

1) 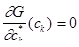;                                                                                                           (2.1.9)

2) 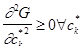.                                                                                                          (2.1.10)

Дифференцируя функцию 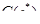, имеем

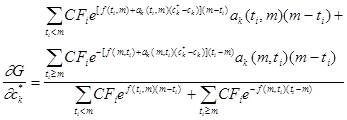,                                            (2.1.11)

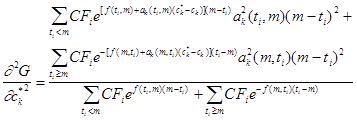.                                          (2.1.12)

Поскольку и числитель, и знаменатель формулы (2.1.12) не содержат отрицательных членов, условие иммунизации второго порядка выполняется для любого портфеля. Условие иммунизации первого порядка выполняется лишь для подмножества портфелей, структура которых удовлетворяет ограничению вида

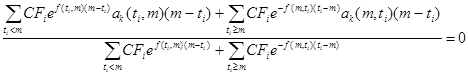.              (2.1.13)

Отсюда

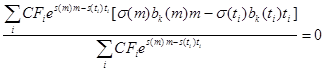,                                                  (2.1.14)

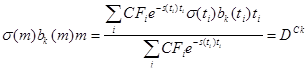,                                                      (2.1.15)

где D^Ck – дюрация портфеля по главной компоненте временной структуры процентных ставок с_k.

Повышение степени гибкости модели описания допустимых сдвигов временной структуры процентных ставок влечет переход от скалярного показателя дюрации Фишера-Вейла D^FW к векторному показателю дюрации D^C, каждая компонента которого D^Ck определяет меру подверженности портфеля воздействию главной компоненты временной структуры процентных ставок с_k. Поэтому структура допустимых портфелей, иммунизированных от непараллельных сдвигов временной структуры процентных ставок, определяется системой не двух, а K+1 уравнений вида

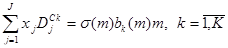,                                                                          (2.1.16)

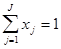,                                                                                                                    (2.1.17)

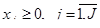,                                                                                                          (2.1.18)

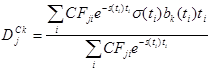,                                                                              (2.1.19)

где 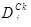 – дюрация облигации выпуска j по главной компоненте временной структуры процентных ставок с_k.

Использование автором векторного показателя дюрации по главным компонентам временной структуры процентных ставок позволяет расширить спектр характеристик рынка, учитываемых в модели иммунизации. Включение диссертантом в рамки анализа таких параметров, как среднеквадратические отклонения спот-ставок для различных сроков вложений s(t_i), а также коэффициенты чувствительности спот-ставок к изменению значений главных компонент временной структуры b_k(t_i), дает возможность использования информации о специфических особенностях рынка ГКО–ОФЗ при определении структуры иммунизирующего портфеля.

Эффективность модели иммунизации определяется степенью точности, с которой портфель, построенный в результате ее использования, аппроксимирует бескупонную облигацию с заданным сроком до погашения. Чем ближе лежит траектория роста рыночной стоимости иммунизированного портфеля к траектории роста цены бескупонной облигации, тем выше степень защиты инвестора от процентного риска. Если даже на коротких временных интервалах доходности иммунизированного портфеля и бескупонной облигации существенно расходятся, то необходимо производить регулярные ребалансировки, то есть часто корректировать структуру портфеля при изменении рыночной конъюнктуры. Эта процедура сопряжена с высокими трансакционными издержками, отрицательно отражающимися на инвестиционной привлекательности стратегии иммунизации. Поэтому оценку эффективности различных моделей иммунизации можно провести путем сравнения характеристик распределения доходностей портфелей, иммунизированных для фиксированных сроков вложений при помощи различных методов, за небольшие промежутки времени, соответствующие различным интервалам ребалансировки.

Для того, чтобы дать оценку эффективности применения моделей иммунизации от параллельных и непараллельных сдвигов временной структуры процентных ставок на российском рынке ГКО–ОФЗ, по данным рыночных торгов, проводимых по средам в течение периода с 6 января 2000 г. по 27 декабря 2000 г., автором были рассчитаны структуры портфелей, иммунизирующих процентный риск для периодов вложений продолжительностью 26, 52, 78 и 104 недели.[65] Если по каким-то причинам торги в среду не проводились, для расчета структур иммунизированных портфелей использовались результаты торгов за четверг. Доли вложений в облигации различных выпусков рассчитывались с использованием трех различных оптимизационных моделей.

Две модели иммунизации опирались на систему уравнений Фишера–Вейла (1.2.20)–(1.2.23), но использовали различные критерии оптимизации структуры портфеля. Первая из них максимизировала значение показателя M², вторая – минимизировала. Исходя из используемого критерия выбора структуры портфеля, первая модель иммунизации получила условное наименование модели Фишера–Вейла, а вторая – модели Фонга–Васичека. Третья модель минимизировала значение показателя M² для портфеля, удовлетворяющего системе ограничений (2.1.16)–(2.1.19), полученной диссертантом. При этом использовалась двухфакторная модель временной структуры, в которой спот-ставки для различных сроков вложений выражались через две первые главные компоненты. Поэтому данная модель получила название двухкомпонентной модели иммунизации.

Определение структур иммунизированных портфелей потребовало предварительного построения временных структур процентных ставок рынка ГКО–ОФЗ по итогам каждой торговой сессии. Для этого были использованы данные Банка России о ценах закрытия облигаций и их купонных характеристиках[66].

Цена каждой облигации P_j выражается через временную структуру процентных ставок s(t) при помощи уравнения

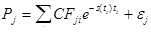,                                                                                             (2.1.20)

где j – порядковый номер выпуска, CF_ji – денежный платеж по облигации выпуска j в момент времени t_i, e_j – случайная ошибка.

Смоделировав временную структуру процентных ставок при помощи нелинейной функции s(t)=f(t, q) с вектором параметров q, можно получить систему уравнений

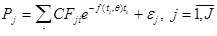,                                                                             (2.1.21)

где J – число выпусков облигаций, данные о ценах которых используются при построении временной структуры процентных ставок.

Оценкой рыночной временной структуры процентных ставок является функция из параметрического семейства f(t,q), обеспечивающая минимальное значение среднеквадратической ошибки при расчете цен облигаций. Поэтому задача построения временной структуры процентных ставок представляет собой задачу оптимизации вектора параметров q с критерием оптимальности

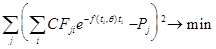.                                                                             (2.1.22)

Расчеты автора показывают, что вполне удовлетворительное качество аппроксимации временной структуры процентных ставок рынка ГКО–ОФЗ достигается при помощи параметрической модели

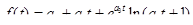.                                                                                   (2.1.23)

Коэффициент детерминации между расчетными и рыночными ценами облигаций превысил 0.99 по итогам 95.44% торговых сессий, состоявшихся в период с 1 мая 1999 г. по 1 апреля 2001 г., а его среднее значение оказалось равным 0.9941. Данные о ценах выпуска 26003, срок до погашения которого существенно превышает сроки до погашения всех остальных инструментов рынка ГКО–ОФЗ, при построении временных структур не использовались.

Значения показателей s(t_i) и b_k(t_i), необходимые при применении двухкомпонентной модели иммунизации, пересчитывались один раз в месяц по данным за последние шесть месяцев. Для этого использовалась выборка 10 спот-ставок для сроков вложений от 0.02 до 4 лет. Построенный ряд коэффициентов чувствительности s(t_i)b_k(t_i) аппроксимировался полиномом шестой степени. Оцененные параметры полинома применялись при расчете показателей дюрации по двум первым главным компонентам временной структуры.

 В ряде случаев система уравнений (2.1.16)–(2.1.19) оказалась неразрешимой. Тогда портфель, иммунизирующий от непараллельных перемещений временной структуры процентных ставок, определялся автором как решение задачи оптимизации

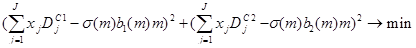,                           (2.1.24)

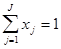,                                                                                                                    (2.1.25)

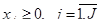.                                                                                                          (2.1.26)

Для каждого иммунизированного портфеля рассчитывалась его рыночная стоимость на дату ребалансировки, наступающую через 4, 8 и 12 недель после момента формирования. При этом автор использовал допущение, что все денежные поступления реинвестируются по спот­-ставкам, установившимся в момент выплаты купона или погашения облигации, для срока, остающегося до момента ребалансировки. Дальнейший анализ проводился путем сравнения выборок доходностей иммунизированных портфелей h_p и доходностей бескупонных облигаций с заданными сроками до погашения h_b за интервал ребалансировки, которые рассчитывались по формулам

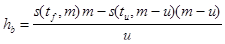,                                                                           (2.1.27)

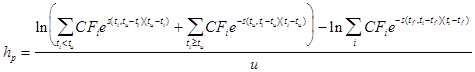,            (2.1.28)

где u – продолжительность интервала ребалансировки, m – срок иммунизации, t_f – момент формирования иммунизированного портфеля, t_u – момент ребалансировки, s(t,t) – спот-ставка для срока вложений t в момент времени t, СF_i – денежное поступление от иммунизированного портфеля в момент времени t_i.

В целях изучения характера связи между доходностями иммунизированных портфелей и доходностями бескупонных облигаций автором были оценены параметры линейного уравнения регрессии

h_p = a + b h_b + e.                                                                                                         (2.1.29)

Оценки параметров a и b, а также коэффициенты корреляции r(h_b,h_p) и основные статистические характеристики распределений доходностей иммунизированных портфелей  и s_p приведены в таблице 2.1.1.

Таблица 2.1.1.

Результаты тестирования эффективности применения моделей иммунизации процентного риска портфелей ГКО–ОФЗ от параллельных и непараллельных сдвигов временной структуры процентных ставок в январе 2000 – марте 2001 г.

название модели	u	m		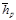sp	r	a	b
Фишера-Вейла	4	26	0.28	0.21	0.7935	0.0575	0.6697
Фишера-Вейла	4	52	0.48	0.43	0.8233	0.0666	0.7273
Фишера-Вейла	4	78	0.65	0.63	0.8539	0.0561	0.7905
Фишера-Вейла	4	104	0.79	0.80	0.8733	0.0517	0.8237
Фишера-Вейла	8	26	0.28	0.20	0.8434	-0.0045	0.9790
Фишера-Вейла	8	52	0.48	0.38	0.8815	-0.0245	1.0013
Фишера-Вейла	8	78	0.63	0.53	0.9020	-0.0117	0.9640
Фишера-Вейла	8	104	0.74	0.64	0.9083	0.0186	0.8928
Фишера-Вейла	12	26	0.28	0.17	0.8835	-0.0288	1.1814
Фишера-Вейла	12	52	0.47	0.32	0.9126	-0.0463	1.1533
Фишера-Вейла	12	78	0.61	0.44	0.9292	-0.0436	1.0932
Фишера-Вейла	12	104	0.71	0.52	0.9354	-0.0180	0.9939
Фонга-Васичека	4	26	0.33	0.22	0.9919	-0.0026	0.9864
Фонга-Васичека	4	52	0.56	0.44	0.9953	0.0152	0.9571
Фонга-Васичека	4	78	0.74	0.66	0.9956	0.0154	0.9570
Фонга-Васичека	4	104	0.88	0.87	0.9896	0.0381	0.9365
Фонга-Васичека	8	26	0.29	0.15	0.9844	-0.0054	0.9970
Фонга-Васичека	8	52	0.49	0.33	0.9914	-0.0006	0.9794
Фонга-Васичека	8	78	0.65	0.52	0.9913	-0.0104	0.9878
Фонга-Васичека	8	104	0.78	0.67	0.9902	0.0227	0.9415
Фонга-Васичека	12	26	0.26	0.12	0.9835	-0.0133	1.0265
Фонга-Васичека	12	52	0.44	0.23	0.9847	0.0288	0.9148
Фонга-Васичека	12	78	0.58	0.35	0.9748	0.0381	0.9006
Фонга-Васичека	12	104	0.73	0.53	0.9890	-0.0060	1.0216
двухкомпонентая	4	26	0.34	0.22	0.9971	0.0044	0.9841
двухкомпонентая	4	52	0.56	0.45	0.9973	0.0054	0.9758
двухкомпонентая	4	78	0.74	0.67	0.9958	0.0121	0.9592
двухкомпонентая	4	104	0.84	0.82	0.9918	0.0410	0.8942
двухкомпонентая	8	26	0.29	0.15	0.9929	0.0037	0.9894
двухкомпонентая	8	52	0.50	0.33	0.9964	0.0002	0.9895
двухкомпонентая	8	78	0.65	0.51	0.9924	-0.0092	0.9851
двухкомпонентая	8	104	0.77	0.64	0.9924	0.0339	0.9178
двухкомпонентая	12	26	0.26	0.11	0.9990	-0.0038	1.0163
двухкомпонентая	12	52	0.45	0.24	0.9981	0.0047	0.9763
двухкомпонентая	12	78	0.59	0.38	0.9971	-0.0097	0.9966
двухкомпонентая	12	104	0.70	0.49	0.9964	0.0116	0.9504

Расчеты автора показывают, что самые низкие значения коэффициента корреляции между доходностями бескупонной облигации и иммунизированного портфеля характерны для модели Фишера–Вейла, критерий оптимальности которой заключается в максимизации показателя M². Это наблюдение свидетельствует о том, что значительная часть перемещений временной структуры процентных ставок на рынке ГКО–ОФЗ достаточно далека от параллельных сдвигов. Портфели с широко распределенными во времени денежными поступлениями, иммунизированные от параллельных перемещений временной структуры, не обеспечивают на рынке ГКО–ОФЗ надежной защиты инвестора от процентного риска. При этом повышенный уровень риска не компенсируется приращением доходности вложений. По итогам проведенных тестов средняя доходность портфелей, иммунизированных с использованием критерия Фонга–Васичека, оказалась равной 55.99%, а средняя доходность портфелей, иммунизированных с использованием критерия максимизации показателя M², составила лишь 53.30%.

Двухкомпонентная модель иммунизации и модель защиты от параллельных сдвигов временной структуры процентных ставок, использующая критерий Фонга–Васичека, оказались способными обеспечить гораздо более высокий уровень эффективности. Коэффициент корреляции между доходностями бескупонных облигаций и иммунизированных портфелей составил 0.9956 при использовании двухкомпонентной модели и 0.9885 при использовании модели Фонга–Васичека. При этом меньшая точность аппроксимации траектории роста цены бескупонной облигации при использовании модели Фонга–Васичека частично компенсировалась небольшим (на 0.25%) превышением средней доходности вложений над аналогичным показателем для портфелей, иммунизированных при помощи двухкомпонентной модели.

Таблица 2.1.1 показывает, что при увеличении интервала ребалансировки коэффициент корреляции между доходностями иммунизированного портфеля и бескупонной облигации возрастает при использовании модели Фишера–Вейла, убывает при использовании модели Фонга–Васичека и остается на приблизительно постоянном уровне при использовании двухкомпонентной модели. Стратегия защиты от непараллельных сдвигов временной структуры процентных ставок, ограничивающаяся использованием критерия Фонга–Васичека, оказывается эффективной лишь при размещении средств на короткие сроки и осуществлении частых ребалансировок, сопряженных с высокими трансакционными издержками. При выборе «гантельных» портфелей, формируемых на основе критерия максимизации показателя M², частые корректировки структуры не требуются, но уровень остаточного риска недопустимо велик. Наиболее эффективное решение проблемы иммунизации обеспечивается двухкомпонентной моделью, при использовании которой можно обойтись без многочисленных ребалансировок при поддержании остаточного процентного риска на минимальном уровне.

Значительная часть перемещений временной структуры процентных ставок рынка ГКО–ОФЗ не соответствует предположению о параллельном сдвиге, использованному в модели иммунизации Фишера–Вейла. Поэтому портфели ГКО–ОФЗ, иммунизированные по методу Фишера–Вейла, не обеспечивают надежной защиты инвестора от процентного риска. Практическое применение разработанной диссертантом модели иммунизации портфеля ГКО–ОФЗ от непараллельных перемещений временной структуры процентных ставок, которая базируется на использовании вектора показателей дюрации по двум первым главным компонентам временной структуры и критерия оптимизации Фонга–Васичека, позволяет инвесторам добиваться более высокого уровня защищенности от процентного риска.

Оптимальная стратегия действий наиболее осторожных участников рынка ГКО–ОФЗ, размещающих свои средства на достаточно продолжительные сроки, заключается в минимизации чувствительности портфеля к воздействию общих факторов сдвига временной структуры процентных ставок. Мы рекомендуем таким инвесторам использовать двухкомпонентную модель иммунизации и осуществлять регулирование остаточного риска в соответствии с критерием Фонга–Васичека.