Для того, чтобы произвести расчет предложенного метода обработки (см. рис. 1.24), предлагается следующий подход к решению данной задачи:

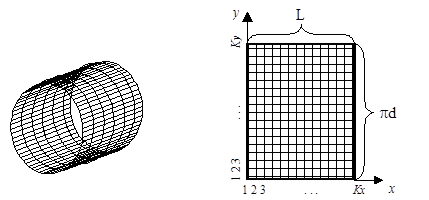
1. обрабатываемую шейку вала, которая является цилиндрической поверхностью разбить на K_x точек по ширине поверхности, и на K_у точек по окружности детали (см. рис. 4.1.а);

2. далее для упрощения расчета произвести развертку цилиндрической поверхности так, как показано на рис. 4.1.б;

а)                                                  б)

Рис. 4.1. Математическая модель обрабатываемой поверхности

Для того чтобы получить геометрию поверхности, необходимо рассчитать координаты каждой точки модели, представленной на рис. 4.1.б. Для более наглядного интерпретации результатов расчета целесообразнее представит результат в виде матрицы размером Кх ´Ку, где каждый элемент матрицы будет численно выражать координаты точки поверхности, относительно максимально углубленной точки в процесс ППД.

При разбиение цилиндрической развертки на точки (Кх ´Ку) следует учесть, что необходимо возможно будет рассчитать геометрию после нескольких оборотов, тогда исходя из рис. 4.1.б., точки (1; 1¼Кх) совпадут с точками (Ку; 1¼Кх), поэтому разбиение целесообразнее производить так, как показано на примере рис. 4.2.

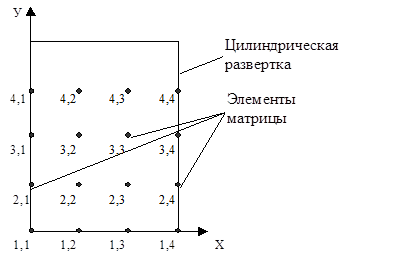
Рис. 4.2. Пример представления цилиндрической развертки в виде матрицы

На рис 4.2 показан пример графической интерпретации матрицы размером 4´4. Очевидно, что для представления микропрофиля поверхности разбиение на такое количество точек неэффективно, значения Кх и Ку должны как минимум быть на порядок выше, но следует также учесть, что увеличение количества рассчитываемых точек приводит к более громоздким расчетам. Детальность расчета микропрофиля можно оценить величинами:

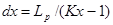;(4.1)

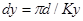,(4.2)

где L_р – ширина обрабатываемого участка, Kx – количество точек рассчитываемых по оси х, Kу – количество точек рассчитываемых по оси у, d – диаметр обрабатываемой детали, dx, dy – интервал между рассчитываемыми точками по оси х, у соответственно, мм.

Как видно из схемы обработки, целесообразнее расчету подвергать расчету геометрию поверхности показанной на рис. 4.3, так как другая часть обработанной поверхности будет идентична, но смещена по оси У на величину:

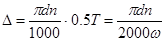,(4.3)

где w – частота колебания инструмента, Гц; Т – период колебания инструмента, с; n – частота вращения детали, об/c.

Поскоку значения Kx – количество точек рассчитываемых по оси х и Kу – количество точек рассчитываемых по оси у не отражают заранее дискретность расчета поверхности, то в качестве исходных данных изначально целесообразнее задавать следующие параметры:

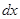 – шаг по ширине детали, мм;

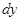– шаг по окружности детали, мм.

Так как параметры Kx и Ky необходимы для проведения дальнейших расчетов, то их значения могут быть найдены по формулам:

,

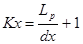где L_р – ширина обрабатываемого участка;

,

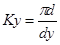где d – диаметр обрабатываемой детали.

Используя все вышесказанное формулу 4.1 можно записать в виде:

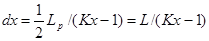,(4.4)

где L – ширина рассчитываемого участка.

Из выше сказанного следует, что элементы матрицы, характеризующие геометрию поверхности обработанной детали численно выражают координаты точек по оси z см. рис. 4.4.

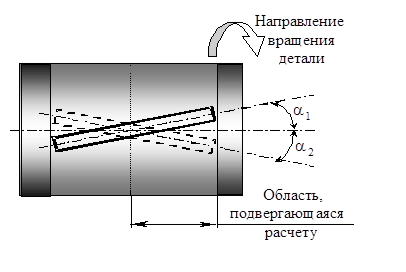
Рис. 4.3. Схема обработки с изображением области, подвергаемой расчету

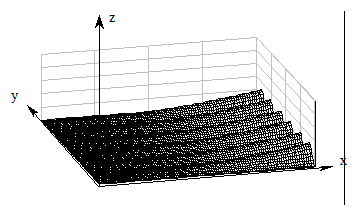
Рис. 4.4. Графическое представление элементов матрицы

Поэтому для того, чтобы рассчитать глубину внедрения индентора, необходимо знать, в каком положении будет находиться инструмент относительно горизонтальной оси во время обработки рассчитываемой точки обрабатываемой поверхности. При этом нас интересуют только те точки инструмента, которые максимально приближены к оси детали (на рис. 4.3 эти точки лежат на оси инструмента), так как именно они будут максимально внедряться в обрабатываемую поверхность, формируя микрорельеф. Поэтому искомое положение инструмента в дальнейшем будем выражать в качестве координаты y, мм см. рис. 4.5.

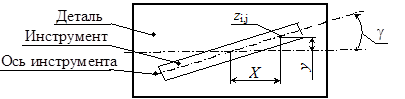
Рис. 4.5. Пояснительная схема к формуле 4.5

Для нахождения y можно использовать выражение:

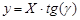.(4.5)

Учитывая то, что инструмент в процессе обработки совершает колебательные движения уравнение 4.5 можно представить в виде функции:

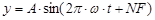,(4.6)

где 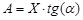 – амплитуда колебания, мм; Х – координата рассчитываемой точки по оси х; a – угол колебания инструмента относительно горизонтальной оси, град.; w – частота колебаний инструмента, Гц; NF – начальная фаза колебания ( характеризует положение инструмента в начальный момент времени); t – время, в которое определяется значение y, с.

Согласно схеме обработке (рис. 4.1.б), инструмент может совершать колебания относительно негоризонтальной оси, а относительно оси, находящейся под определенным углом 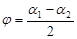, град. (рис. 4.6).

Отрезок AB (рис. 4.6) характеризует интервал, на котором попадают в зону обработку точки с постоянной координатой по оси x равной X. Тогда, чтобы рассчитать значения у, можно задать положение точек инструмента участвующих в процессе обработки на отрезке AB гармоническим колебанием «точки» O согласно рис. 4.7 с амплитудой OA.

Поэтому уравнение 4.6. запишется в следующем виде:

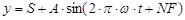,(4.7)

где 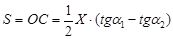 – параметр уравнения, вводимый из-за неравенства углов a₁ и a₂; 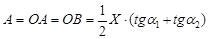– амплитуда колебания, мм; a₁ и a₂ – максимальное отклонения инструмента относительно горизонтальной оси в процессе колебания по часовой и против часовой стрелки соответственно, град.

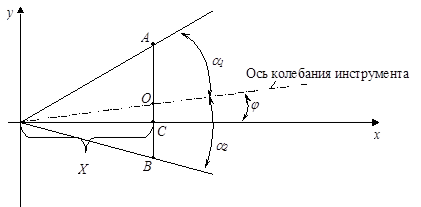
Рис. 4.6. Пояснительная схема для интерпретации колебания инструмента

Но расчет значения координаты y усложняется тем, что помимо колебания инструмента в процессе обработки имеет место вращательное движение детали. Зная частоту вращения детали и координаты рассчитываемой точки значение координаты y можно записать в следующем виде:

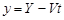,(4.8)

где Y – координата рассчитываемой точки по оси y; 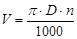 – окружная скорость детали, мм/с; D – диаметр детали, мм; n – частота вращения детали об/с.

Объединяя формулы 4.7 и 4.8 для расчета положения инструмента при обработке рассматриваемой точки можно воспользоваться следующей системой нелинейных уравнений:

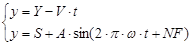(4.9)

где y, t – неизвестные.

Анализируя систему нелинейных уравнений, можно прейти к выводу, что при отыскании ее решений может получиться несколько ответов, поскольку во втором уравнении системы присутствует периодическая тригонометрическая функция sin (см. рис. 4.7).

Для нахождения всех элементов матрицы, характеризующей развертку геометрии обработанной поверхности, систему уравнений 4.9 представится в следующем виде:

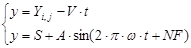,(4.10)

где 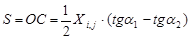 – параметр уравнения, вводимый из-за неравенства углов a₁ и a₂; 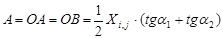– амплитуда колебания, мм.

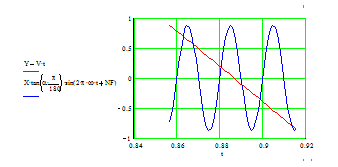
Рис. 4.7. Графическое решение системы 4.9 при: X=10 мм, Y=25 мм, n=20 об/с, w=50 Гц, a=5 град, D=2 мм, NF=0 рад

Для расчета координаты рассматриваемой точки используем выражение:

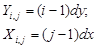,(4.11)

где i, j – индексы элементов матрицы.

Значение у непосредственно влияет на глубину внедрения индентора. Поэтому координату z обрабатываемой точки (см. рис. 4.8) можно определить из следующего выражения:

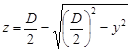(4.12)

Учитывая то обстоятельство, что в процессе обработки, каждая точка может обработаться не один, а несколько раз (данное высказывание следует из того, что нелинейная система уравнений 4.9 имеет несколько корней (см рис. 4.7) необходимо найти максимальное внедрение инструмента в обрабатываемую поверхность детали, подходя к этой задаче с математической точки зрения необходимо найти минимальные значения z_i,j, так как они и будут формировать геометрию детали после обработки.

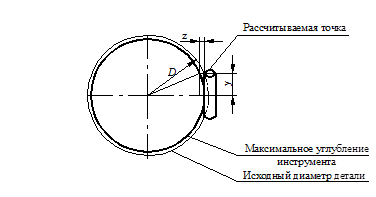
Рис. 4.8. Схема для вывода формулы 4.12