Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Натуральными называют числа, которые были придуманы людьми для счета элементов реальных множеств (животных, людей, различных предметов), а также для Фиксированиярезультатовиз^рения~величин?длинт,т_г масзсы, времени, пло­щади и ДР0Г

Как и многие математические понятия, понятие натураль­ного числа возникло из потребностей практики. Уже в глубо­кой древности нужно было сравнивать между собой различные множества. Простейшим способом такого сравнения было ус­тановление взаимно однозначного соответствия между множе­ствами, при котором каждому элементу из одного множества ставился в соответствие единственный элемент из другого. Ес­ли такое соответствие имело место, то множества считались равночисленными (все пары — полные). Если часть элементов второго множества оставалась без пары, то считали, что в пер­вом множестве меньше элементов, чем во втором.

Со временем для сравнения стали применять множества-по­средники (пальцы, камешки, узелки...) — их называют «чис­ловые фигуры»; на следующем этапе в результате процесса абстрагирования появилось понятие числа: один, два и т. п.

После того как понятие натурального числа сформирова­лось, числа стали самостоятельными объектами науки «мате­матика» и появилась возможность изучать числа и действия с ними, независимо от характера породивших их множеств. В математике говорят: число — это общее свойство класса конечных равномощных (т. е. равночисленных) множеств. Наука, изучающая числа и действия с ними, получила назва­ние «арифметика» («агШшюз» в переводе с греческого означает «число»).

Каждое множество равномощно только одному числу сюда мы знаем, что если при повторном пересчете объе* получаются различные результаты, это означает ош» счета). Поскольку число обозначает количественную хара ристику множества, его называют — количественное ни ральное число. (Если мы хотим получить ответ на вощ «Сколько?», речь идет о количественном числе.)

При счете элементов множества происходит процесс нумерации. Счет — это процесс упорядочивания множе путем присвоения каждому элементу определенного номе

В этом случае натуральное число обозначает собой пог ковый номер некоторого элемента и называется в силу Э1 числом порядковым. Эти две роли натурального числа на отражение в русском языке: порядковые натуральные 41 выражаются порядковыми числительными — первый, вте третий т. д.; количественные — количественными числш ными один, два и т. д.

 

 

Правила счета. Принцип построения натурального ряда чисел

Итак, счет — это процесс нумерации элементов множеств. Этот процесс подчиняется определенным правилам:

• первому отмеченному предмету ставится в соответствии число 1;

• на каждом следующем шаге выбирается предмет, ещ< отмеченный ранее;

• ему ставится в соответствие число, следующее за пос ним из уже названных.

В основе построения множества натуральных чисел (обоа начается Ш) лежит следующий принцип: каждое число начиная со второго, на единицу больше предыдущего.

Усвоение ребенком этого принципа является центрально задачей изучения нумерации первого десятка в школе. П скольку тема «Числа в пределах 10» изучается в любой совре менной альтернативной дошкольной математической програм ме, с точки зрения преемственных связей имеет смысл сделать усвоение этого принципа центральной задачей изучения это: темы в ДОУ.

 

Этапы изучения темы «Числа в пределах 10». Примеры заданий

Прежде всего отметим, что с методической точки зрения изучение темы «Числа в пределах 10» целесообразно разделить на два этапа:

1-й этап (подготовительный): основное внимание уделя­ется формированию умения устанавливать взаимно одно­значное соответствие между сравниваемыми множествами. Следует предлагать детям сравненивать равночисленные (эквивалентные) и неравночисленные множества путем уста­новления взаимно однозначного соответствия, что постепенно подводит ребенка к пониманию смысла количественной харак­теристики множества, которую мы называем числом.

Приведем примеры заданий, которые воспитатель может использовать для всех возрастов, варьируя количество пред­метов от 5-6 для младшей и средней группы до 10 в старшей группе.

Упражнение 1

Материалы. Фланелеграф и картонные модели фигур. Способ выполнения. Педагог выкладывает на фланелегра-фе несколько фигур двух видов: кружки и квадраты. Задание.

Определить, чего больше, кружков или квадратов?

Фигурки надо выставлять на фланелеграф вразброс, чтобы ребенок сам понял необходимость установления взаимно од­нозначного соответствия и самостоятельно выполнил его лю­бым способом, и их должно быть достаточное количество для того, чтобы ответ нельзя было дать сразу, опираясь на визу­альное восприятие, без установления взаимно однозначного соответствия. Например, так:

Подобная ситуация необходимо выводит ребенка на п способа сравнения количественного состава множеств без ресчета элементов. Если в группе есть хорошо считающие до ти, то следует взять еще больше предметов и сделать их визу ально похожими, чтобы затруднить счет (например, сдела их разноцветными и т. п.). Работа на фланелеграфе удобна те что дети могут составлять пары любым образом — выстраив парные предметы напротив друг друга или расставляя пре меты произвольными парами:

При этом хорошо видно, что считать пары нет надобности оставшиеся без пары фигуры («лишние») покажут, каких бы ло больше (и на сколько больше).

Данные задания являются также базовыми для подготовка к пониманию ребенком смысла отношений «больше на «меньше на», «столько же».

К выводу «столько же» ребенок подведен самим процессо выполнения действий по образованию пар: если все фигур имеют пару, то их — равное количество: «одинаково», «круж ков столько же, сколько квадратиков»; если остались фиг ки без пары, то этих фигур больше, и больше именно на сталг ко, сколько осталось без пары.

Не следует форсировать или сокращать этот этап и старать быстрее перейти на способ сравнения множеств на основе п ресчета. Должно пройти достаточно времени, чтобы у ребен сформировался устойчивый стереотип правильных действи в подобных ситуациях и чтобы этот стереотип успел интериори зироваться, т. е. перейти во внутренний план действий, чтоб ребенок легко мог выполнять эти действия «в уме» и четко пред ставлял себе смысл и образ ситуации (т. е. легко образовыв пары в уме в любых заданных ситуациях).

Полезно предлагать детям уравнять сравниваемые множества.

Упражнение 2

Материалы. Фланелеграф и модели фигур Способ выполнения. Педагог предлагает предметную ситуацию.

□ □□□□□□□

О О о о о о

Задание. Как сделать, чтобы кружков стало столько же, сколько квадратов (квадратов столько же, сколько кружков)?

Уравнять эти множества можно двумя способами: убрать два квадратика или добавить два кружка. Понимание и «виде­ние» вариантов выполнения такого задания поможет ребенку в дальнейшем без проблем справляться с простыми задачами вида «больше на», «меньше на», «на сколько больше?», «на сколько меньше? ».

Приведем примеры упражнений для младшей группы (3-4 года).

Упражнение 1

Цель. Подготовить ребенка к восприятию сравнения по типу «один к одному» (взаимно однозначное соответствие). Развивать координацию, соласованность движений рук, формировать соревновательную мотива­цию и учить ребенка активному общению со взрослым, понимать словес­ную инструкцию и действовать по правилам.

Воспитатель играет с одним или двумя-тремя детьми. Он учит ребят прятать руки за спиной и одновременно с командой: «Один... Много...» выбрасывать их перед собой с соответствующим количеством пальцев. Играйте с детьми, пока им весело (1-2 мин). Постепенно воспитатель до­бавляет сравнение количества пальцев прикладыванием. Например, по команде «Много!» у воспитателя — три пальца, у ребенка — пять пальцев. Выиграл тот, кто «выкинул» больше. Проверяя, воспитатель поясняет ребен­ку, как узнать, у кого больше (прикладывает один палец к одному: у меня — больше нет, а у тебя еще два пальца осталось, значит, у тебя больше...).

Упражнение 2

Цель. Учить различать размер предметов, готовить к пониманию смыс­ла взаимно однозначного соответствия при сравнении множеств. Разви­вать деятельность общения и учить действовать по инструкции. Учить са­мостоятельно проводить сравнение разнородных множеств по количеству.

Воспитатель, используя подходящие игрушки, разыгрывает с детьми сюжет: мама-гусыня привела гусят домой и кормит их обедом. На столе большие и маленькие миски (кукольный набор). Какую миску дадим маме-гусыне? {Большую.) Почему? (Она — большая.) Какую гусенку? (Малень­кую.) Почему? (Он — маленький.)

— Маша, собери все остальные большие миски и поставь их в ш они не нужны маленьким гусятам.

— Ваня, помоги Маше. Где еще лишняя большая миска?

— Петя, возьми все маленькие миски для гусят. Дай каждому гус миску.

— Дети, всем гусятам хватило мисок? {Нет. Одному еще нужно.)

— Сколько нужно мисок? (Одна.) Вариант:

— Пришел папа-гусь (соседка-гусыня). Какую ему миску поста большую или маленькую? (Большую.)

— Сколько надо добавить больших мисок? (Одну.)

Упражнение 3

Цель. Готовить к пониманию смысла сравнения множеств с помощью взаимно однозначного соответствия. Устанавливать причинно-следствен ■ ную связь. Развивать мелкую мускулатуру руки, тактильную чувствитель ность и координацию.

Для организации упражнения необходимы таз с влажным песком и ку сок клеенки, дети на полу (на клеенке) делают «куличи» для гусыни и гусят, Пользуются большой и маленькой формами. При их изготовлении воспита­тель помогает детям провести предварительное соотнесение размера и формы будущего «кулича»: из большой формы получится большой кулич для гусыни. Из маленькой формы получится маленький «кулич»—для гусенка,

— Какой кулич получится из этой мисочки? Из этой? Сделай, сравни их. Сколько надо больших куличей? (Один.) Маленьких? (Много.) Сделай каждому гусенку один кулич. Какому гусенку этот «кулич»? Этот? Этот?

Упражнение 4

Цель. Учить сравнивать предметы по цвету, сравнивать множества с помощью взаимно однозначного соответствия. Включать ребенка в сю­жетное игровое взаимодействие с персонажами на основе принятия учеб­но-игровой задачи.

Воспитатель, используя подходящие игрушки, разыгрывает с детьми сюжет:

— Сегодня Мы снова играем с Мишей и Мишуткой. У Миши красный фартук (кепка, рубашка), у Мишутки — желтый. Миша любит все красное, Мишутка — все желтое. Разделите им игрушки.

Игрушки должны быть подобраны по цветам и оттенкам красного и жел­того. Дети по очереди подходят и, выбирая подходящую игрушку, ставят ее возле медведя, объясняя свой выбор. (Мяч — красный. Это для Миши. Кегля — желтая. Это — для Мишутки.)

Затем подводится итог: почему у Миши этот мяч? (Потому что он крас­ный. У Миши все игрушки красные. У Мишутки — желтые.)

А теперь медведи дадут игрушки детям: каждый — по одной. Воспита­тель предлагает каждому ребенку взять одну игрушку у Миши, одну — у Мишутки.

Когда игрушки разобраны, ситуация анализируется. Подбор игрушек должен быть таким, чтобы у всех детей оказалось по две игрушки: крас­ная и желтая — в этом случае делается вывод, что игрушек поровну.

Вариант. У последнего ребенка оказались две красных игрушки, и боль­ше игрушек нет, значит, красных — больше (и наоборот).

Упражнение 5

Цель. Учить сравнивать предметы по цвету, сравнивать множества с помощью взаимно однозначного соответствия. Включать ребенка в сю­жетное игровое взаимодействие с персонажами на основе принятия учеб­но-игровой задачи.

Используя подходящие игрушки, воспитатель разыгрывает сюр­призную ситуацию: персонажи нашли коробку. В ней игрушки двух цве­тов: синие и зеленые. С этими игрушками выполняем действия, анало­гичные предыдущему упражнению. Можно использовать любую другую пару кукол, обозначив цвета (синий и зеленый).

Вариант. У кого игрушек больше? Воспитатель показывает детям дру­гой прием сравнения множеств по количеству: путем выкладывания пара­ми. Не следует выкладывать игрушки в два ряда: один напротив другого — это может привести к тому, что ребенок будет оценивать не количество, а их пространственное расположение:

 

О О О О О

 

Выкладывайте хорошо опознаваемые пары:

 

После того как все пары определены, подводится итог: зеленые игру! > • ки закончились, а синие еще остались. Каких было больше?

Упражнение 6

Цель. Подготовить к восприятию смысла взаимно однозначного со<н ветствия при сравнении разнородных множеств.

Упражнение подобного типа можно провести с водой. Органинун игровую ситуацию, педагог просит ребенка налить воду в одинакошиЩ!! ведерки: для одно персонажа сделать ведерко легче, для другого — тял | лее. Воду наливать в два ведерка одной кружечкой, чтобы ребенок сам отмеривал количество воды для получения более тяжелого и более л§К| кого ведерка.

Вариант. Можно предложить ребенку подумать, как сделать ведерки одинаковыми по тяжести. Для этого не нужно уметь считать. Если реб§< нок догадается, что нужно наливать воду по очереди в каждое ведерко, м> он сможет самостоятельно сделать вывод: надо налить в них одинаково» количество кружек воды, тогда ведерки будут одинаковыми по тяжести.

Упражнение 7

Цель. Обучать установлению взаимно однозначного соответствия м« жду множествами.

Разыгрывается игровая ситуация «Гости». Ставим стол и стулья. (Если нет игрушечной мебели, можно использовать подходящие коробки.) При­ходят гости (куклы). Дети рассаживают их на стулья, приговаривая: «Не один стул — одна кукла».

Воспитатель предлагает детям расставить на столе тарелки, чашки, разложить яблоки, произнося при этом:

— Каждому по одной тарелке. Тарелок столько же, сколько гостей.

— Каждому по одной чашке. Чашек столько же, сколько гостей.

— Каждому по одному яблоку. Яблок столько же, сколько гостей.

2-й этап — активное использование приема пересчета. Про­водится с опорой на определение числа как характеристики класса эквивалентных множеств, т. е. их общего свойства, не­зависимого от характера входящих в них объектов.

Полезны задания:

а) Что общего у данных множеств? Чем они похожи?

б) Выберите похожие множества. Чем они похожи?

В процессе выполнения таких заданий у ребенка постепен­но формируется понятие о некоторой общей, абстрактной характеристике множеств разнородных объектов (предме­тов ) — количестве. Эту характеристику называют словом «число».

Символом числа является цифра. После знакомства ребен­ка с цифрами упражнения приобретают традиционный вид: «Найди число, соответствующее даньому множеству».

 

 

Следует помнить, что выполнение задания в таком виде предполагает умение считать;

Умение считать подразумевает: знание слов-числительных, знание их порядка при счете, понимание смысла процесса нумерации элементов множества, понимание того, что по­следний названный номер является характеристикой количе­ственного состава множества, и умение соблюдать правила счета.

Как видно, большая часть нагрузки при освоении счета при­ходится на механическую память, т. е. процесс обучения счету в большой мере репродуктивен (опирается на память, а не на мыслительные операции). Для того чтобы ребенок не осваи­вал его на формальном уровне, на первых порах этот процесс следует обязательно сопровождать предметными действиями: откладыванием, показыванием, а также проговариванием вслух.

 

При формировании операции счета полезно такое задание. Посмотрите на круги на фланелеграфе:

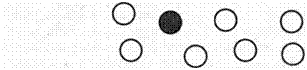
а) Можно ли посчитать круги так, чтобы темный кружок
был третьим? Пятым? Седьмым?

б) Который пО счету темный кружок?

В традиционной методике, давая подобное задание, педагог обычно выстраивает модель так:

 

 

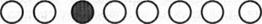
Вопрос формулируется следующим образом: «Который по счету темный кружок? Какой он по счету справа? Слева? и т. п.».

Чтобы ответить на поставленный таким образом вопрос, ре­бенку надо всего лишь вспомнить названия числительных по порядку. Смысл процесса нумерации предметов множества, процесса счета здесь не затрагивается и потому ребенком не осмысливается. Не случайно дети, незнакомые с приведенной выше формой упражнения, обычно спрашивают: «Ас какой стороны считать? » — и еще чаще пытаются сначала располо­жить предметы в ряд, будучи твердо убеждены, что считать их можно только в таком положении и причем единственным способом — слева направо.

Это показывает, что процесс счета сформирован у ребенка в «механическом» формальном виде, главные свойства опера­ции счета и ее смысл ребенком не понят.

Следует помнить, что можно предлагать ребенку посчитать двойками, десятками и т. п., но нельзя говорить: «Посчитай от 10 обратно». Процесс счета «векторный», т. е. возможен по определению только в сторону увеличения номеров, и слово — числительное, названное при счете последним, является отве­том на вопрос «Сколько?», т. е. характеризует количество пред­метов данной совокупности. Перечисление названий чисел в обратном порядке не является счетом.

Умение называть числительные в обратном порядке явля­ется базовым для обучения ребенка процессу отсчитывания, поэтому формировать такое умение необходимо, но форму­лировать задание следует в виде: «Назови числа в обратном порядке». (А не «посчитай»!) Таким же образом формулиру­ются задания: «Назови числа от 6 до 9» и т. п. (А не «посчитай от 6 до 9».)

В период обучения счету для ребенка очень важна непосред­ственная работа руками с сосчитываемыми предметами. Желательно дать детям возможность прикасаться к сосчиты­ваемым предметам, двигать их, составляя уже сосчитанную группу, или показывать пальцем на каждый сосчитываемый предмет. Это позволит формировать правильное представление о самом процессе на уровне кинестетики, на уровне «памяти ощущения».

Уже при запоминании правильной последовательности на­зывания числительных полезно обращать внимание ребенка на изменение количественного состава сосчитываемой группы, показывая ее руками:

 

 

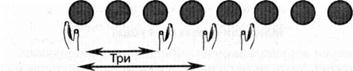
Четыре

Пять

При этом ребенок сначала проговаривает:

— Три да еще один — четыре.

— Да еще один — пять...

Затем речевое сопровождение заменяется только движени­ем руки: либо «еще один» придвигается к сосчитываемому мно­жеству (на столе), либо производится охватывающее движе­ние руками новой совокупности (с «еще одним»). Эти приемы готовят ребенка к пониманию на уровне кинестетики основно­го принципа построения натурального ряда — каждое следую­щее число на единицу больше предыдущего.

Следствием этого принципа является идея бесконечности ряда натуральных чисел (как бы ни было велико число, все­гда можно найти следующее, добавив к нему единицу), а так­же способ нахождения значений выражений вида 5 + 1,8 + 1; 6-1, 7 - 1 и т. п. путем называния либо следующего, л предыдущего числа. Иными словами, для нахождения зняч ния данных выражений нет необходимости выполнять какой то прием арифметических действий, достаточно понимать, чт добавление 1 ведет к получению следующего по счету числи, а убавление 1 — к появлению предыдущего по счету числи Именно для получения результатов в таких выражениях р#к' бенок заучивал наизусть названия чисел в прямом и обратном порядке.

Методическое выделение двух этапов при работе над темой «Числа в пределах 10» не означает, что первый этап необходи мо реализовывать на младшем возрасте, а второй — на стар­шем. Речь идет о необходимой последовательности заданий, которая может быть реализована как на серии тематически взаимосвязанных занятий, так и внутри одного занятия. По­кажем, как может быть организована такая последователь­ность действий ребенка на серии взаимосвязанных упражне­ний (фрагменте занятия):

 

Младшая группа (3-4 года)

Цель занятий. Учить детей соотносить количественный состав мно­жества с обозначающим его словом — числительным.

Фрагмент 1 .Упражнение 1

Цель. Развивать внимание и активизировать мыслительную деятель-
ность детей. Учить умению сравнивать предметы по самостоятельно вы-
бранному признаку «размер» и на этой основе производить классифика-
цию множества. _ч

Материалы. Две коробочки — побольше и поменьше, а также горсть пуговиц или камешков. Пуговицы (камешки) двух размеров: крупные и мелкие.

Задание. Разложить пуговицы в две коробочки.

— Как вы думаете, какие пуговицы нужно сложить в маленькую коро­бочку? В коробочку большего размера?

Способ выполнения. Педагог подводит детей к самостоятельному вы­бору основания для классификации, в данном случае — по размеру.

Упражнение 2

Цель. Учить соотносить слово — числительное с количественным со­ставом множества.

Способ выполнения. Используя коробку с большими пуговицами, пе­дагог играет с детьми в «Оладушки». Читая текст потешки, раздает играю­щим по одной пуговице, называя детей по имени.

Бабушка, бабушка Испекла оладушки. Один — Ванечке, Один — Мишеньке и т. д.

Затем пуговицы возвращаются в коробку (съели оладушки), при этом их можно считать (пока этот счет в устах педагога звучит для детей как еще одна приговорка: одна, две, три...).

Варианты. Детям раздают по 2, затем по 3 пуговицы в соответствии с текстом:

Бабушка, бабушка Бабушка, бабушка

Испекла оладушки. Испекла оладушки.
Ване — два, Ване — три,

Мише —два... Мише —три...

Каждому ребенку дают столько пуговиц, сколько он попросит:

Бабушка, бабушка Испекла оладушки. Ване? (Ребенок отвечает.)

— Три! Мише?

— Два! и т. д.

Фрагмент 2 . Упражнение 1

Цель. Формировать счетную деятельность, развивать конструктивные умения, восприятие и внимание. Формировать умение работать по об­разцу и по представлению.

Материалы. Счетные палочки.

Способ выполнения. Дети используют счетные палочки для воспроиз­ведения сложенных педагогом на фланелеграфе фигурок (педагог исполь­зует узкие полоски бархатной бумаги вместо палочек).

Задание. Взять из коробочки одну палочку.

— Ваня, сколько у тебя палочек? (Одна.) А в коробке? (Много.)

— Возьмите еще одну папочку. Кто сосчитает, сколько у него пал (Две.) А в коробке? (Много.)

— Возьмите еще одну палочку. Сосчитаем палочки. (Педагог пом детям, подсказывая название числительного.) Сколько у Вани пал (Три.) У Пети? И т. п.

— Сложите из палочек такую фигурку:

 

      Дети складывают фигурки, дают им названия или придумывают, на это похоже. Пусть каждый ребенок попробует сложить свою фигурку. К но складывать буквы и называть их. В этот раз дети работают только с мя палочками. Педагог обращает на это внимание детей:

— Чем похожи все-все наши фигурки? Вы заметили? (Все сложен трех палочек.)

Упражнение 2

Цель. Формировать счетную деятельность и развивать конструкт ные умения, восприятие и воображение. Формировать умение рабо по представлению.

Задание. — Сложите такую бабочку, как на карточке:

 

Материалы. Счетные палочки двух цветов и контурный рисунок на I точке, соответствующий размеру палочек. Карточка выдается каждому бенку.

Дети накладывают палочки на контурный рисунок и замечают, что па­лочек не хватает. Педагог помогает сосчитать, сколько еще нужно палочек.

— Возьмите из коробки еще три палочки.

Каждый ребенок достраивает свою бабочку, ориентируясь на схема­тический рисунок.

Упражнение 3

Цель. Развивать внимание, конструктивную деятельность и простран­ственное мышление.

Задание. Сложить рядом такую же бабочку, но красную.

Ребенок ориентируется на образец, но уже работает без контурной опоры.

— Кто сосчитает бабочек? Какую бабочку вы сложили? (Красную.)

— Теперь сложите такую же, но зеленую. Кто сосчитает бабочек? Ка­кие у нас есть бабочки?

Упражнение 4

Цель. Развивать внимание, конструктивную деятельность, простран­ственное мышление, гибкость мышления и воображения.

Материалы. Фланелеграф, полоски бархатной бумаги вместо палочек для педагога, счетные палочки у детей.

Способ выполнения. Педагог предлагает образцы конструкций, пере­страивая каждую на глазах детей, чтобы они видели, что количество па­лочек не меняется.

— Посмотрите, как я бабочку переделаю в домик (педагог складывает на фланелеграфе бабочку, а затем переделывает ее в домик):

— Сложите такой домик из папочек красной бабочки.

— Посмотрите, как я переделаю домик в щетку: I__ I ц!

— Сложите такую же щетку из палочек зеленой бабочки.

— Посмотрите, как щетку я переделаю в треугольник: /^Ч I

— Переделайте у себя щетку в такой треугольник. ^--

— Сколько оладушек поместится внутрь треугольника?

Педагог дает детям по очереди коробочку с пуговицами и предваряет работу вопросами:

— Как ты думаешь, две поместятся? Бери, пробуй. Есть еще место? Еще одна поместится? Две? Бери, пробуй...

Много поместилось? Больше двух? Больше трех?

 

Средняя группа (4-5 лет)

Цель занятий. Формировать понятие о равных совокупностях. Исполь­зовать различные способы образования равных совокупностей (взаимно однозначное соответствие и пересчет).

Фрагмент 1 Упражнение 1

Цель. Учить уравнивать множества с помощью установления взаимно однозначного соответствия.

Материалы. Фланелеграф и картонные модели фигур у педагога, лы или изображения сказочных героев.

Способ выполнения. На фланелеграфе выставлены две группы о ковых кругов двух цветов (8 и 10). Круги стоят так, чтобы затруднить ресчет для тех детей, кто умеет это делать.

Воспитатель, используя куклы, разыгрывает сюжет:

— Гунька й Незнайка поспорили, у кого ягод собрано больше. Решил проверить: взяли две корзинки и стали раскладывать — одну ягоду из Гунь киной кучки в корзинку Гуньке, одновременно с ним Незнайка кладет ягО ду из своей кучки в свою корзинку.

Рассказывая это, педагог выставляет кукол (рисунки), корзинки (коробочки) и раскладыва­ет ягоды по корзинкам. Удобно пригласить ре­бенка — помощника (за Гуньку).

К концу рассказа на фланелеграфе возле Незнайки осталось два кру­жочка, а возле Гуньки — ни одного.

— Ну вот, — сказал Гунька, — ты посчитал, сколько у тебя ягод, Не знайка?

— Нет, — говорит Незнайка.

— А вы, дети, посчитали? Так как установки на подсчет не было, дети, скорее всего, тоже н

посчитали. Во всяком случае, большинство не считало. Гунька вдру «вспомнил», что он тоже не считал.

— Что же делать? — расстроился Гунька.

— Знаешь, я хоть и не считал, — говорит Незнайка, — но думаю, что у меня больше, чем у тебя, на две ягоды.

— Почему это у тебя больше, — возмутился Гунька, — ты же не считал, откуда ты знаешь?

— Как вы думаете, дети, почему Незнайка так решил? Проговаривается способ сравнения: в каждую корзинку положили по одной ягоде одновременно, значит в них ягод поровну, т. е. в одной столькоже, сколько в другой. Две оставшиеся ягоды означают, что в этой куче ягод было больше, так как им нет пары.

Упражнение 2

Цель. Учить устанавливать отношения «больше на...» и «меньше на...» с помощью взаимно однозначного соответствия.

Способ выполнения. Педагог продолжает разыгрывание сюжета. По­скольку Гунька «не верит» Незнайке, педагог просит детей расставить кружки на доске так, чтобы доказать Гуньке, что у Незнайки ягод больше.

— Как вы поставили круги? (Один под другим. Парами.)

— В каком ряду кругов больше? Меньше? На сколько больше в верх­нем ряду? На сколько меньше в нижнем ряду?

Педагог обращает внимание детей на то, что считать фигурки для от­вета на этот вопрос нет необходимости. Разницу показывает число фигу­рок, оставшихся без пары.

Упражнение 3

Цель. Уравнивать множества разными способами. Способ выполнения. Педагог продолжает развивать сюжет:

— Что надо сделать, чтобы кругов стало поровну (чтобы Гуньке не бы­ло обидно)?

Следует рассмотреть с детьми три варианта уравнивания:

а) два добавить в нижний ряд;

б) два убрать из верхнего ряда;

в) один из верхнего ряда переставить в нижний.

Варианты предлагаются детьми, педагог активизирует предложения:

— А по-другому можно?

Упражнение 4

Цель. Закреплять умение сравнивать множества установлением вза­имно однозначного соответствия.

Материалы. Фигурки из «Дидактического набора», фланелеграф и кар­тонные модели фигур у педагога.

Задание.

— Достаньте из коробочки («Дидактический набор») пять квадратов. Выложите их в ряд. Поставьте треугольников на два меньше. Если дети справляются, педагог спрашивает, обязательно ли было считать треу| ники? Если есть затруднения, выносит задание на фланелеграф и п гает выполнению наводящими вопросами.

— Поставьте ниже полукругов столько же, сколько треугольн Сколько их?

К этому времени два круга из каждого набора надо аккуратно р; лить пополам или добавить в набор четыре полукруга из плотного к; на (размер тот же), это нужно для новых конструктивных заданий.

Упражнение 5

Цель. Формировать конструктивные умения с использованием пг. ма сравнения множеств. Развивать внимание и воображение.

Способ выполнения. Педагог показывает детям аппликацию, орк тируясь на которую они складывают конструкцию.

Задание.

— Сложите из этих фигур такой же самолет: Гунька полетел на поиски Незнайки, который улетел на воздуш- ( О ( ном шаре... Каких фигур здесь одинаковое количество? Чего больше, треугольников или квадратов?

Упражнение 6

Цель. Формировать конструктивные умения с использованием при** | ма сравнения множеств. Развивать внимание, воображение и гибкость мышления.

Способ выполнения. Педагог показывает детям аппликацию, ориен тируясь на которую они перестраивают свою конструкцию в новую

— Самолет у Гуньки можно перестраивать. Долетел он до реки, пере« строил самолет в катер и поплыл по реке. Постройте катер. Какие фигуры остались лишние? (Три полукруга и два квадрата.) Уберите их в коробочку. Посмотрите на свой катер: о каких фигурах можно сказать словами «столько же»? (Квадратов столько же, сколько треуголь­ников.)

Упражнение 7

Цель. Формировать умение распознавать геометрические фигуры, развивать пространственное мышление, мелкую моторику и двигатель-но-моторную координацию, внимание, воображение и восприятие.

Материалы. Альбомный лист, цветные карандаши, рамка с прорезями в форме геометрических фигур.

Задание. Используя рамку, нарисовать катер. Раскрасить по рамке.

Фрагмент 2 Упражнение 1

Цель. Обучать умению установливать взаимно однозначное соответ­ствие для сравнения множеств без пересчета.

Материалы. Фланелеграф и картоннье модели фигур.

Способ выполнения. Педагог испольгует игровой сюжет:

- Жили в сказочном Цветочном городе два друга — Незнайка и Гунька. Вот такие домики были у всех жителей Цветочного города (на фланеле­графе собирается домик из двух деталей):

Это Незнайкин домик.

А это Гунькин домик.

Педагог выставляет на фланелеграфе еще 5-6 квадратов вразброс.

— Это — Знайкин домик, это — доктора Пилюлькина, это — Винтика и Шпунтика...

— Чего не хватает у домиков? (Крыш.)

— Сколько надо крыш для одного домика? (Одну.)

— Кто хочет «достроить» домики? (Треугольников красного цвета долж­но быть больше, чем выставленных «домиков».)

Дети и педагог наблюдают за «строителем».

— Скажи словами, что надо сделать, чтэбы получился домик? (На каж­дый домик поставить крышу.) Уточняем, что только одна крыша нужна одному домику.

Обычно дети не используют здесь пересчет. Выполняя задание, они ставят на домик крышу, пока есть свободные домики.

Упражнение 2

Цель. Обучать умению установливать езэимно однозначное соответ­ствие для сравнения множеств без пересчета и с использованием пе­ресчета.

Материалы. Фланелеграф и картонные модели фигур. Способ выполнения. Педагог выставляет оставшиеся «свободными» крыши.

— А теперь что нужно сделать, чтобы получились домики? (Каждой «крыше» добавить квадрат, будет домик.)

— Можете вы мне сразу сказать, сколько квадратов надо достать из конверта? (Остальные квадраты в конверте.)

— Что для этого надо сделать? (Сосчитать «свободные» кры четыре. Значит, квадратов надо четыре.)

Педагог отдает конверт ребенку и следит за действиями ребенка, лагая детям также наблюдать за действиями отвечающего: он д сначала достать указанное количество квадратов, а затем расставит «под крыши».

Упражнение 3

Цель. Обучать умению сравнивать множества путем образования П Материалы. Фланелеграф и картонные модели фигур. Способ выполнения. Педагог выставляет зеленые треугольники в роне от домов — это «кусты» (их девять).

— Решили веселые человечки посадить кусты возле домов, Незна говорит, что их хватит, а Гунька — что нет. Как вы думаете, хватит или хватит им этих кустов, чтобы посадить по одному кусту возле каждого мика?

Тот из детей, кто может использовать пересчет, пробует это сдела Задание рассчитано на то, что большая часть затруднится это сдел и возникнут разногласия.

— Что придется сделать, чтобы выяснить, кто прав: Незнайка или Гу ка? (Надо поставить возле каждого дома по одному кусту.)

После расстановки «кустов» педагог спрашивает:

— Ну что, получилось посадить возле каждого дома по кусту? (Не Одинаковое ли количество домов и кустов? Чего больше? Чего меньш Почему Петя уверен, что домов больше?(Одному дому куста не хватил значит, кустов меньше.) На сколько меньше? (На один.)

Модель убирается с фланелеграфа.

 

Упражнение 4

Цель. Установливать взаимно однозначное соответствие путем визу ального соотнесения элементов множества и путем пересчета.

Материалы. Фланелеграф и картонные модели фигур, «Дидактический набор» счетного материала.

Способ выполнения. Педагог использует игровой сюжет. Он выстав­ляет на фланелеграф пять кружков.

— Возьмите из коробочки столько квадратов, сколько у меня кругов.

— Сколько у вас квадратов? (5) Это будут домики. Сколько крыш пона­добится для этих домиков? (5)

— Возьмите из коробки сразу все нужные вам крыши. Покажите их мне на ладони, я посмотрю, правильно ли вы взяли. Достройте домики.

— Теперь надо посадить возле каждого домика елочку: ,/*,

— Сколько у нас домиков? (5) Сколько надо елочек? (5)

— Сколько треугольников надо на одну елочку? (2) Положите на ла­донь два треугольника. Сколько из них получится елочек? (?) Положите на ладонь еще два треугольника. Сколько теперь получится елочек? (2) «По­садите» эти две елочки у домиков.

— Сколько еще надо елочек? (3) Положите на ладонь сразу столько треугольников, сколько вам понадобится для трех елочек. Покажите мне.

Наблюдая за детьми, педагог видит, кто понял смысл задания, кому на­до индивидуально помочь наводящими вопросами, как это делалось выше.

— Можно ли сказать, что домиков столько же, сколько елочек? (Да.)

Елочек столько же, сколько домиков? (Да.)

Упражнение 5

Цель. Учить выделять равночисленные множества различными спосо­бами. Использовать умение устанавливать взаимно однозначное соответ­ствие множеств в конструктивной деятельности.

Материалы. Аппликация или рисунок для анализа, «Дидактический ма­териал» для конструирования.

Способ выполнения. Педагог показывает детям сю­жетную аппликацию: «Незнайка летит на ракете». Можно кратко напомнить детям сюжет сказки для создания иг­ровой атмосферы.

— О чем здесь можно сказать словами «столько же»? (Квадратов столь­ко же, сколько треугольников.)

— Будем строить такую же ракету: Гунька полетел к Незнайке в гости. Возьмите столько же квадратов, сколько у меня на рисунке. Покажите мне на ладони. Сколько их? Поставьте, как нужно. Возьмите столько же тре­угольников. Покажите мне на ладони. Сколько взяли? Постройте (сложи­те) ракету.

Упражнение 6

Цель. Использовать умение устанавливать взаимно однозначное ответствие множеств в конструктивной деятельности (деятельности ко структивного рисования).

Материалы. Контурная рамка с геометрическими прорезями, ал ные листы, цветные карандаши.

Задание. Нарисовать такую же ракету, используя рамку. Закрасить р сунок по рамке.

Педагог оказывает детям помощь индивидуально, помогая двига и поворачивать рамку для рисования деталей в нужном положении.

Во всех приведенных упражнениях дети выполняют дейс вия с предметами и группами предметов, учатся замечать и вы­делять различные качества и свойства предметов и их совокуп" ностей, убеждаются в значимости этих свойств, постепенно учатся выделять количественные соотношения между множе­ствами.

Выделенные количественные характеристики педагог учит детей соотносить со словом — числительным, обозначающим это количество.

Цифры. Примеры заданий

Знакомство детей с цифрами не представляет сложной ме­тодической проблемы, поскольку дети 3-4-летнего возраста легко запоминают символические изображения: буквы, циф­ры, знаки. Нет особой необходимости заучивать с детьми оп­ределенный объем символики наизусть в дошкольный пери­од, но и искусственно отгораживать ребенка от нее тоже нет смысла, поскольку с изображениями цифр он сталкивается в повседневной жизни постоянно — от номера своей квартиры и телефона бабушки до номера нужного канала телевидения или автобуса и т. д. и т. п.

Цифра — это лишь символ, знак числа, и в этом ее главная роль. Ранняя символизация ради манипулирования символа­ми не имеет смысла, если ребенок не понимает сущности про­цесса счета как процесса нумерации элементов пересчиты­ваемого множества. Момент для знакомства детей с цифрами педагог определяет сам, когда видит, осознанно или нет дети считают (достаточно и счета до 3). Если это так, то уже можно знакомить детей с цифрами. Помните, что цифры — понятие вторичное, на формирование процесса счета умение раз­личать цифры не влияет: считают предметы, а не цифры!

В связи с этим лучше не смешивать процесс обучения счету со знакомством с цифрами. При знакомстве с цифрами целе­сообразно помнить, что дошкольник не должен уметь писать цифры и тем более «вписываться» в клетки (это школьная за­дача). Умение узнать цифру и соотнести ее с количеством пред­метов — это вполне достаточный уровень подготовки к школе по любой программе. В связи с этим можно обозначить основ­ные цели работы педагога при знакомстве детей с цифрами:

— научить детей узнавать образ цифры в различных изо­бражениях (печатная цифра, письменная цифра, стилизован­ная цифра типа цифры на почтовом индексе и т. п.);

— научить детей соотносить слово — числительное и цифру. Полезно учить детей запоминать контур цифры не только

визуально (глазами), но и двигательно-осязательно (кинесте-зически). Для этого используют изображения цифр, выре­занные из мелкой наждачной бумаги, которые дети обводят пальцем по ходу письма цифры (последнее наиболее важно, по­скольку не только готовит руку к письму цифр, но и формиру­ет правильный мыслеобраз ее контура, помогающий освоить ее написание).

Приведем пример фрагментов занятий, цель которых — зна­комство ребенка 3-4 лет с цифрами.

Фрагмент 1 Упражнение 1

Цель. Познакомить детей с изображениями цифр 1 и 2.

Материалы. Кубики, фишки, геометрические фигурки из картона или пластика, карточки и т. п. На них написаны цифры 1 и 2, а также разные значки, буквы, символы (10-20 шт.). На карточках, фишках и плоских фи­гурках цифры и другие знаки пишем с двух сторон, на кубиках — со всех сторон.

Примечание. Используется прием знакомства сразу с двумя цифра­ми, поскольку удобно организовать сравнение двух непохожих контуров, чтобы ребенок запоминал их «на контрасте». Поскольку цифры — это условные обозначения, принятые по соглашению, при знакомстве с их изображениями используется метод показа.

Задание. Найти цифру, которую педагог показал ребенку среди раз­личных изображений:

— Вот цифра 1. Ее пишут, когда хотят обозначить только один предмс 11 один нос, один медведь... Найдите такую же цифру на кубиках и карточках, Сколько единиц Ваня нашел? Сколько Петя нашел? И т. п.

Вариант. Показывают детям сразу две цифры 1 и 2. Просят найти таи кие же.

Педагог просит детей показать среди предметов, используемых в уп­ражнении, такие, которых только по одному. (Только один красный кубик. Только один зеленый треугольник.) Рядом с указанным детьми предме­том педагог кладет карточку с цифрой 1. Можно предложить желающим детям сделать это.

— Найдите предметы, которых у нас по два. (Два больших синих тре­угольника. Два желтых кубика.) Рядом кладем карточку с цифрой 2.

Вариант. Если дети легко выделяют показанные им цифры, распозна­ют их в любом положении (в том числе вверх ногами), можно показать им на этом же занятии цифру 3 и добавить упражнение на ее распознавание.

Упражнение 2

Цель. Закреплять представление о графическом образе цифры.

Материалы. Цифры, вырезанные из мелкой наждачной бумаги и при­клеенные на картон.

Способ выполнения. Ребенку завязывают глаза и обводят его паль­чиком цифру в той последовательности, как она пишется. Ребенок дол­жен угадать цифру.

Сначала ребенок угадывает контур цифр 1 и 2, затем можно добавить цифру 3.

Упражнение 3

Цель. Закреплять навыки счета в пределах трех. Г~ I I У Материалы. Фигурки «Дидактического набора»: — '—' ^-—' Фигурки окрашены в три цвета: квадраты — красные, треугольники — зеленые, кружки — желтые.

Задание. Куклам, сидящим за столом, надо раздать «печенье» (фигур­ки) на тарелки.

Педагог просит одного ребенка раздать куклам по 1 «печенью», затем другого — по 2, по 3. Каждый раз гости «съедают» печенье, т. е. раздавать надо на чистые тарелки, приговаривая: «Мишке — два, Кате — два, зайцу — два» и т. д.

Вариант. Усложняя упражнение, педагог просит раздать: по два оди­наковых, по два разных и т. д. При этом каждый ребенок самостоятельно выбирает фигурки из коробочки. Можно помочь ребенку, подсказывая: правильно, это два кружка. А что это? Правильно, два треугольника.

Если ребенок при этом учитывает не только форму, но и цвет, это пре­красно, если нет, то это — третий этап усложненного задания (все это не следует делать на одном занятии).

Упражнение 4

Цель. Учить соотносить цифры и соответствующее количество пред­метов.

Материалы. Фигурки «Дидактического набора», карточки с цифрами.

Способ выполнения. Продолжая сюжет предыдущего упражнения, педагог «за гостя» заказывает нужное количество «печений», кладя возле куклы карточку с цифрой. Дети должны положить рядом нужное количест­во фигурок.

Фрагмент 2

Цель занятий. Учить детей различать цифры 1,2 и 3; соотносить циф­ру и обозначаемое ею количество предметов.

Упражнение 1

Цель. Учить распознаванию графического образа цифры.

Материалы. Треугольники, квадраты и круги, на которых написаны циф­ры: 1,2,3 соответственно. Фигурки помещены в коробочку.

Способ выполнения. Педагог предлагает детям по очереди выбрать из коробочки фигурки с заданной цифрой.

— Петя, найди все единицы! Катя — все двойки. И т. п.

Игру можно оформить любым сюжетом, например: Мартышка, Слоне­нок и Попугай делят фигурки. Мартышке — с единицей, Попугаю —сдвой­кой, Слоненку — с тройкой.

Задания предлагаются последовательно: сначала надо выбрать все 1, затем среди оставшихся фигур предлагаем другому ребенку найти все 2, затем 3. На этом этапе дети могут заметить, что тройки написаны на всех оставшихся фигурках, поэтому отбирать их специально не нужно.

Когда группировка выполнена, предлагаем ребенку, выполнявшему за­дание, вопрос: «Здесь у тебя все единицы, а что общего еще есть у этих фигурок?» (Это все треугольники.)

Если ребенок это замечает, рассматриваем следующие две группы, лая обобщение: «Это все кружки. Это все квадратики».

Другому ребенку предлагаем сделать это же упражнение (предвари тельно все смешав), но выбрать сначала тройки и т. д.

Интересно, если ребенок учел результаты предыдущей работы и с зу отобрал все кружки, зная, что только на них тройки и т. д.

Упражнение 2

Цель. Развивать конструктивные умения, учить соотносить ци< с обозначаемым количеством предметов.

Материалы. Фигурки из «Дидактического набора», фланелеграф, фи­гуры из картона для воспитателя.

Способ выполнения. Дети воспроизводят образцы конструкций, ори­ентируясь на фланелеграф. Педагог складывает на фланелеграфе «ма­шину» (сопровождая процесс словами: квадратик, квадратик, кружок...).

 

Педагог ставит рядом с машиной карточку с цифрой 2 и предлага детям найти, каких фигурок здесь две? (Два кружка.)

Упражнение 3

Цель. Развивать конструктивные умения, пространственное мышле­ние. Познакомить с названиями порядковых числительных.

Способ выполнения. Сопровождая сюжет игрушками или рисунками «Ежик» и «Зайчик», педагог дополняет конструкцию сюжета на фланеле­графе, делая паузу после каждой фигуры, чтобы дети повторили его дей­ствия:

— Ежик поехал в магазин за продуктами, а в домике остался его ждать Зайчик. Кто покажет, в какую сторону едет машина? (Ребенок пальцем показывает направление движения. Это направление определяется из конструкции машины. Не следует подсказывать детям решение этих ма­леньких конструктивных задач, пусть подумают самостоятельно.)

— Едет Ежик по лесу мимо елок:

 

— Покажите самую высокую елку, самую низкую

— Приехал в магазин:

— Купил хлеб, молоко, морковку, капусту, яблоки и поехал обратно. По­кажите, куда он теперь едет? В какую сторону? Кто запомнил, что Ежик купил?

 

— Покажите большой домик, маленький домик. Давайте сосчитаем ел­ки: первая, вторая, третья.

Педагог берет ребенка за руку и, показывая его пальцем на елки, назы­вает порядковые числительные, побуждая всех детей повторять их назва­ния (считаем в направлении от большого домика, так как движение маши­ны идет в ту сторону).

— Кто хочет теперь сам сосчитать елки по порядку? Кто запомнил, как надо считать?

— Кто помнит, что Ежик привез из магазина?

 

Упражнение 4

Цель. Учить соотносить цифру с обозначаемым количеством предметов.

Материалы. Карточки с цифрами и фигурки «Дидактического набора». Способ выполнения. Педагог показывает детям карточку с циф­рой (1, или 2, или 3) и предлагает показать на фигурках, сколько яблок  (морковок) съел зайчик сразу, сколько положил в суп и т. п. И наоборот: выкладывая на фланелеграфе 2, 1, 3 фигурки (обозначающие морковки, яблоки и т. п.), предлагает детям найти и поставить рядом соответствую­щую цифру.

Как видно из приведенных упражнений, работа по форми­рованию представлений о численных характеристиках пред­метов и множеств может удачно сочетаться с другими задачами предматематической подготовки ребенка: формированием про­странственной ориентации, подготовкой к формированию представлений о величинах, об арифметических действиях и т. п. При этом математическое содержание выступает в дан­ных текстах занятий не как материал для заучивания и запо­минания ребенком словесных образов и определенных способов действий, а как средство развития познавательных процессов (внимания, восприятия, воображения, мышления), формиро­вания активной познавательной деятельности малыша.

Становясь старше, ребенок уже может активно восприни­мать содержательно более «нагруженные» познавательные блоки. В связи с этим перечень понятий расширяется, однако все они продолжают быть взаимосвязанными, позволяют при разработке занятия использовать вещественное моделирова­ние как основу формирования математических представлений ребенка и являются преемственными с предыдущим содержа­нием обучения, а также с тем содержанием, которое предпо­лагается к изучению на следующем возрастном этапе.

Приведем примеры занятий для разных возрастных групп, в которых работа с численными характеристиками и их сим­волическим обозначением проводится на геометрическом ма­териале.

 

Средняя группа (4-5 лет)

Цель занятий. Уточнять представление о геометрических формах; формировать умение определять численные характеристики множеств и обозначать их цифрой. Формировать классификационные умения.

Упражнение 1

Цель. Развивать восприятие и внимание. Уточнять представление о форме геометрических фигур.

Материалы. Конверты с геометрическими фигурами по форме фигур из рамки на каждого ребенка. Фигуры вырезаны из тонкого цветного кар­тона. Счетные палочки. Карточки с рисунками флажков у педагога.

Способ выполнения. Педагог показывает карточки с флажками, дети должны сложить такие же. Для палочки можно использовать счетные па­лочки.

Карточки по одной выставляются на фланелеграф.

Упражнение 2

Цель. Учить определять количественную характеристику множества. Формировать счетные умения.

Способ выполнения. Педагог организует беседу:

— Сколько флажков в верхнем ряду? (4) В нижнем ряду? (4) Попробу­ем сосчитать все флажки. (8)

— Флажки в верхнем ряду считаем по порядку (хором). (Первый, вто­рой....) Кто хочет посчитать сам?

Аналогично работаем со вторым рядом, предоставляя инициативу детям. Можно предложить желающим попробовать назвать порядковые номера в обратном порядке (это чисто мнемоническое действие хорошо удается детям с хорошей механической памятью).

Упражнение 3

Цель. Уточнять представление о треугольной и четырехугольной форме. Способ выполнения. Педагог организует беседу:

— Покажите флажки треугольной формы. Сколько их? (3) Кто может показать флажки четырехугольной формы? Сколько их? (4)

— Один флажок нельзя назвать ни треугольным, ни четырехуголь­ным — он имеет округлую форму. Кто видит этот флажок?

Упражнение 4

Цель. Уметь производить классификацию по заданному признаку, ределять количественную характеристику объекта.

Способ выполнения. Дети сначала выполняют задание на столэ своими флажками, а затем на фланелеграфе.

— Переставьте флажки так, чтобы в верхнем ряду были все треуг ные, а во втором ряду все четырехугольные флажки. Флажок с ок лыми сторонами поставьте в третий ряд ниже. Кто сделает это на фла: леграфе?

Педагог показывает две карточки с числами 3 и 4 и предлагает де определить, к какой группе какая относится и почему.

Упражнение 5

Цель. Развивать восприятие, воображение, внимание и конструкт ную деятельность.

Способ выполнения. Дети выполняют задание, ориентируясь на зец. Педагог показывает на карточке контурный рисунок лодочки, д складывают ее из своих фигур.

 

А

Упражнение 6

Цель. Развивать зрительно-моторную координацию. Уточнять пр? ставление о форме геометрических фигур. Развивать воображение и про­странственное мышление.

Материалы. Рамка с прорезями в форме геометрических фигур. Аль­бомные листы, цветные карандаши и восковые мелки.

Способ выполнения. На альбомном листе дети рисуют лодки с помо­щью рамки (карточки на фланелеграфе и на столах остаются в качестве образцов) и раскрашивают их. Затем восковыми мелками дополняют на рисунке фон: море, небо, облака, дорисовывают чаек.

 

Старшая группа (5-6 лет)

Тема занятий. Число и множество.

Цель занятий. Уметь производить классификационные действия, как основу соотношения числа и множества.

Упражнение 1

Цель. Учить самостоятельно выделять основание для классификации. Материалы. Фланелеграф, модели квадратов двух размеров одного цвета.

Способ выполнения.

— Разделите фигуры на две группы так, чтобы в каждой группе были похожие.

Примечание. Так как цвет фигур и форма одинаковы, то разделить можно только по размеру. Не следует подсказывать детям основание для классификации. Материал, организованный таким образом, сам являет­ся подсказкой, поскольку других вариантов нет.

Упражнение 2

Цель. Учить самостоятельно соотносить количественные характери­стики множества и отдельной фигуры с их цифровыми обозначениями.

Материалы. Фланелеграф, фигуры, карточки с цифрами.

Способ выполнения. Из данных чисел выбрать число, которое подхо­дит к каждой группе, и объяснить свой выбор: 2, 4, 3, 5, 7, 8.

Могут быть выбраны числа 3 и 5 {больших квадратов 3, малень­ких — 5). Может быть выбрано число 8 {всего 8 фигур), число 4 (это все четырехугольники). Два последних числа подходят только ко всему мно­жеству. Поэтому вопрос следует задать так:

— А теперь я снова все соединю в одну группу. Какое число подойдет ко всем квадратам (всему количеству)? (8) Мне кажется, что к ним еще подойдет число 4, как вы думаете?

Если дети замечают, что у всех квадратов 4 угла, то делаем обоб­щение:

— Какое же можно дать им всем название, кроме названия «квадрат»? ( Четырехугольник.)

Если дети этого не замечают, наталкивать их на обобщение не следует.

 

Число и цифра О. Десяток

Наиболее сложными понятиями в данной теме являются число и цифра 0.

Знакомство ребенка с нулем представляет отдельную м#"я дическую проблему, поскольку нуль не является натуральны* числом. При знакомстве с нулем нельзя ссылаться на счет п |им1 метов, невозможно выстроить предметную модель нуля. В тематике нуль определяют как символ пустого множест

Для знакомства с нулем можно использовать следую ситуацию.

Педагог выставляет на фланелеграф несколько изобр; ний любых предметов или фигур и просит детей обозначит количество цифрой. Затем ситуация изменяется: предм убираются или добавляются, при этом конечный результат же обозначается цифрой. В один из моментов педагог сни с фланелеграфа все фигуры и просит детей обозначить ци конечный результат. Поскольку на фланелеграфе не ост, ни одной фигуры, для обозначения пустого множества п добится цифра 0. В данной ситуации педагогу легко объяс ее появление необходимостью обозначить отсутствие п метов, подлежащих счету.

Вопрос о месте нуля среди других чисел является важ для правильного формирования представления о натураль ряде. В школе данный вопрос рассматривают после знакомо ва со всеми числами первого десятка и после того, как ребенок освоился с тем, что числа в ряду располагаются в определен" ном порядке, у каждого из них есть свое, четко определенн: место, которое не может меняться ни при каких обстоятельст­вах. Имеет смысл следовать той же методической последова­тельности и при изучении чисел с дошкольниками.

При этом не стоит располагать последовательность ци 0123456789 на стене группы для того, чтобы она часто попадалась на глаза ребенку. Ребенок фиксирует (запомина­ет) ряд в таком виде, будучи убежден, что нуль — первое чис­ло в ряду, т. е. что нуль — натуральное число. В дальнейшем этот стереотип бывает трудно преодолеть.

Вопрос о месте нуля в ряду чисел связывается с процессом построения количественной модели натурального ряда чисел. Построение этой модели возможно после того, как дети осво­ятся с процессом установления взаимно однозначного соответ­ствия между множеством предметов, его численной харак­теристикой и цифровым обозначением этой количественной характеристики. Количественной моделью натурального ря­да может служить, например, лесенка из кубиков, где каждая следующая ступенька содержит на один кубик больше, или любой счетный материал — палочки, кружки и т. п. В этой модели важна наглядность «с первого взгляда», т. е. здесь полезнее выстраивать такие модели, которые сразу позволя­ют увидеть, что разница между соседними группами состав­ляет один предмет. Такие модели называют количественны­ми моделями натурального ряда. Например:

1 2 3 4 5 6 7

 

При построении такой модели важно, чтобы ребенок пони­мал ее смысл и умел строить ее самостоятельно. Технология ее построения отражает принцип построения натурального ря­да чисел: каждая следующая группа — это «столько же и еще один». Понимание этого принципа избавляет от постоянного утомительного пересчета элементов модели. Таким образом, понимание общего принципа построения натурального ряда де­лает сложные и громоздкие на первый взгляд моделирующие действия совсем простыми.

Опираясь на смысл этой модели, устанавливают место нуля в ряду чисел: поскольку его модель — это пустое множество, т. е. в нем нет ни одной фигурки, то это число можно поста­вить только перед числом один. В школе подтверждение этого дедуктивного (теоретического) вывода о месте числа нуль в ря­ду чисел ищут в операции сравнения чисел, для подтвержде­ния чего сравнивают нуль с другими числами. Реально это можно сделать только после знакомства со знаком сравнения и всеми цифровыми обозначениями однозначных чисел, по­скольку процесс сравнения чисел нужно записывать (ведь нуль никак не обозначишь соответствующим количеством пред­метов).