Имеем фактические данные об изменении объемов выполнения СМР (собственными силами) и изменении численности рабочих промышленно-производственного персонала (таблица 5).
Таблица 5 – Фактические данные об изменении выполнения объемов СМР и изменении численности рабочих ППП
Изменение
численности
рабочих ППП,
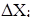
| -1 | -5 | 0 | -10 | +1 | -8 | -6 | +6 | -1 | 0 | -1 | +5 | +2 | -1 |
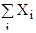 =
=-19 =
=-19
|
Изменение
объемов выполнения
СМР,
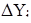
| -71 | -472 | +94 | -1078 | +26 | -625 | -466 | +494 | -90 | -51 | -267 | +235 | +39 | -59 |
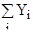 =
=-2291 =
=-2291
|
Требуется определить зависимость изменения объема выполнения СМР от изменения численности рабочих ППП, составив соответствующее уравнение регрессии.
Значение 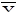 и
и 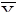 определяем по формулам:
определяем по формулам:
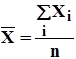 ;
; 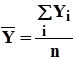 ; n=14, i=1, ... ,14; (2.3.1), (2.3.2)
; n=14, i=1, ... ,14; (2.3.1), (2.3.2)
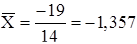 ;
; 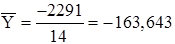
Дальнейшим вычислениям придается табличная форма, что повышает их наглядность (таблица 6).
Таблица 6
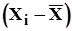
| 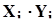
| 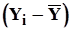
| 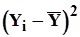
| 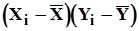
|
| +0,357 | +71 | +92,643 | 8582,725 | 33,074 |
| -3,643 | +2360 | -308,357 | 95084,039 | 1123,344 |
| +1,357 | 0 | +257,643 | 66379,622 | 349,622 |
| -8,643 | +10780 | -914,357 | 836048,729 | 7902,788 |
| +2,357 | +26 | +189,643 | 35964,467 | 446,989 |
| -6,643 | +5000 | -461,357 | 212850,281 | 3064,795 |
| -4,643 | +2796 | -302,357 | 91419,755 | 1403,844 |
| +7,357 | +2964 | +657,643 | 432494,315 | 4838,280 |
| +0,357 | +90 | +73,643 | 5423,291 | 26,291 |
| +1,357 | 0 | +112,643 | 12688,445 | 152,857 |
| +0,357 | +267 | -103,357 | 10682,669 | -36,898 |
| +6,357 | +1175 | +398,643 | 158916,241 | 2534,174 |
| +3,357 | +78 | +202,643 | 41064,185 | 680,273 |
| +0,357 | +59 | +104,643 | 10950,157 | 37,357 |
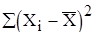 =
=269,208 =
=269,208
| 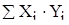 =
=25666 =
=25666
| 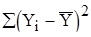 =
=2018549,208 =
=2018549,208
| 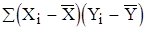 =
=22556,791 =
=22556,791
|
Теснота связи между показателями объема выполнения СМР и численности рабочих ППП измеряется коэффициентом корреляции, который исчисляется по формуле:
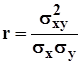 . (2.3.3)
. (2.3.3)
Подставляя соответствующие значения в формулы:
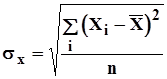 ; (2.3.4)
; (2.3.4)
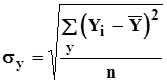 ; (2.3.5)
; (2.3.5)
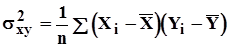 , (2.3.6)
, (2.3.6)
получим:
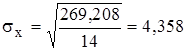 ;
;
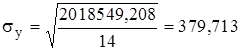 ;
;
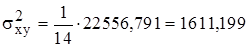 ;
;
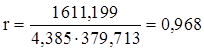 .
.
Считая формулу связи линейной, определим зависимость объема выполнения СМР от численности рабочих ППП. Для этого решается система нормативных уравнений:
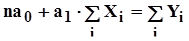 ; (2.3.7)
; (2.3.7)
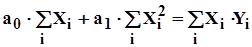 . (2.3.8)
. (2.3.8)
Величина 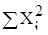 и
и 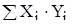 представлена в таблице 7.
представлена в таблице 7.
Таблица 7
| 1 | 25 | 0 | 100 | 1 | 64 | 36 | 36 | 1 | 0 | 1 | 25 | 4 | 1 | 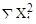 =295 =295
| |
| 71 | 2360 | 0 | 10780 | 26 | 5000 | 2796 | 2964 | 90 | 0 | 267 | 1175 | 78 | 59 |  =25666 =25666
|
Значение а0 определяем из первого уравнения :
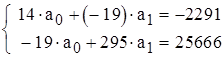
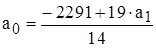 , или
, или 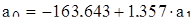 .
.
Подставляя найденное выражение 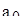 во второе уравнение, находим
во второе уравнение, находим 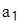 :
:
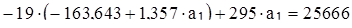 а1
а1
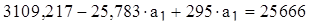
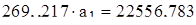
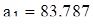
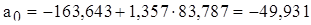
Итак, уравнение регрессии в окончательном виде получило следующий вид:
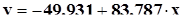
Анализ зависимости объема работ от выработки
одного работника ППП по СМУ-21
Имеем фактические данные об изменении объемов выполнения СМР (собственными силами) и выработки одного рабочего ППП (таблица 8).
Таблица 8 – Фактические данные об изменении объема выполнения СМР и изменении выработки одного рабочего ППП
Изменение выработка 1 рабочего ППП,
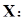
| Изменение объема выполнения СМР,
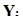
|
| 1 | 2 |
| +8,1 | +1594 |
| 3,4 | 678 |
| 0,5 | 83 |
| 0,3 | 71 |
| 3,0 | 589 |
| +4,1 | +798 |
| 2,3 | 472 |
| +0,8 | +163 |
| 1,3 | 246 |
| +0,8 | +218 |
| +0,4 | +94 |
| +2,0 | +435 |
| 2,8 | 611 |
| +1,2 | +299 |
| 1,8 | 433 |
| +0,6 | +179 |
| +1,8 | +450 |
| 4,4 | 1078 |
| +2,9 | +640 |
| +0,1 | +26 |
| +2,3 | +448 |
| 3,2 | 625 |
| 2,6 | 466 |
Продолжение таблицы 8
| 1 | 2 |
| –0,92 | 170 |
| +2,8 | +494 |
| 0,7 | 136 |
| 0,5 | 90 |
| +0,9 | +137 |
| 0,4 | 51 |
| 1,6 | 267 |
| +1,4 | +235 |
| +0,3 | +39 |
| 0,5 | 59 |
| 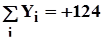
|
Требуется определить зависимость объема выполнения СМР от выработки 1 рабочего ППП, составив соответствующее уравнение регрессии. Значения 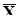 и
и 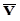 определяем по формулам:
определяем по формулам:
; n=33, i=1...33 (2.3.9)
n=33, i=1...33 (2.3.10)
; .
Дальнейшим вычислениями придаем табличную форму (таблица 9).
Таблица 9
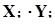
| 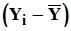
| 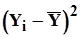
| 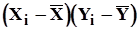
| |
| 1 | 2 | 3 | 4 | 5 |
| +8,091 | +12911,4 | +1590,242 | +25288696 | +12866,648 |
| 3,409 | +23052,0 | 681,758 | +464793,97 | +2324,113 |
| 0,509 | +41,5 | 86,758 | +7526,95 | +44,160 |
| 0,309 | +21,3 | 74,758 | +5588,759 | +23,100 |
| 3,009 | +1767,0 | 592,758 | +351362,04 | +1783,609 |
| +4,091 | +3271,8 | +794,242 | +630820,35 | +3249,244 |
| 2,309 | +1085,6 | 475,758 | +226345,67 | +1098,525 |
| +0,791 | +130,4 | +159,242 | +25358,014 | +125,960 |
| 1,309 | +319,8 | 249,758 | +62379,058 | +326,933 |
| +0,791 | +174,4 | +214,242 | +45899,634 | +169,465 |
| +0,391 | +37,6 | +90,242 | +8143,619 | +35,285 |
| +1,991 | +870,0 | +431,242 | +185969,66 | +858,603 |
| 2,809 | +1710,8 | 614,758 | +377927,39 | +1726,855 |
| +1,191 | +358,8 | +295,242 | +87167,838 | +351,633 |
| 1,809 | +779,4 | 436,758 | +190757,55 | +790,095 |
| +0,591 | +107,4 | +175,242 | +30709,758 | +103,568 |
| +1,791 | +810,0 | +446,242 | +199131,92 | +799,219 |
| 4,409 | +4743,2 | 1081,758 | +1170200,3 | +4769,471 |
| +2,891 | +1856,0 | +636,242 | +404803,88 | +1839,376 |
| +0,091 | +2,6 | +22,242 | +494,707 | +2,024 |
| +2,291 | +1030,4 | +444,242 | +197350,95 | +1017,758 |
| 3,209 | +2060,0 | 628,758 | +395336,62 | +2017,684 |
| 2,609 | +1211,6 | 469,758 | +220672,57 | +1225,599 |
Продолжение таблицы 9
| 1 | 2 | 3 | 4 | 5 |
| –0,929 | +156,4 | 173,758 | +30191,842 | +161,421 |
| +2,811 | +1393,1 | +490,242 | +240337,21 | +1378,070 |
| 0,709 | +95,2 | 139,758 | +19532,298 | +99,088 |
| 0,509 | +45,0 | 93,758 | +8790,563 | +47,723 |
| +0,891 | +123,3 | +138,242 | +17753,43 | +118,719 |
| 0,409 | +20,4 | 54,758 | +2998,439 | +22,396 |
| 1,609 | +427,2 | 270,758 | +73309,894 | +435,650 |
| +1,391 | +329,0 | +231,242 | +53472,562 | +321,658 |
| +0,291 | +11,7 | +35,242 | +1241,999 | +10,255 |
| 0,590 | +29,5 | 62,758 | +3938,567 | +31,944 |
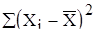 =
=+197,291 =
=+197,291
| 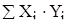 =
=+40177 =
=+40177
| 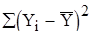 =
=+8269177,912 =
=+8269177,912
| 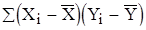 =
=+40176,251 =
=+40176,251
|
Теснота связи между показателями объема выполнения СМР и выработки одного рабочего ППП измеряется коэффициентом корреляции, который исчисляется по формуле:
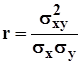 . (2.3.11)
. (2.3.11)
Подставляя соответствующие значения в формулы:
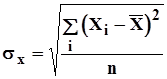 ; (2.3.12)
; (2.3.12)
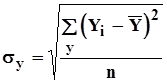 ; (2.3.13)
; (2.3.13)
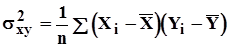 , (2.3.14)
, (2.3.14)
получим:
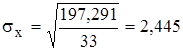 ;
;
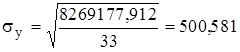 ;
;
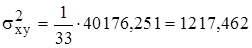 ;
;
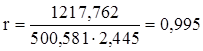 .
.
Считая формулу связи линейной, определим зависимость выполнения объема СМР от выработки одного рабочего ППП.
Для этого решается система нормативных уравнений:
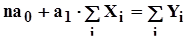 ; (2.3.15)
; (2.3.15)
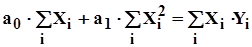 . (2.3.16)
. (2.3.16)
Величина 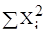 и
и 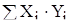 представлена в следующей таблице (таблица 10).
представлена в следующей таблице (таблица 10).
Таблица 10
| |
| 1 | 2 |
| 65,61 | 12911,4 |
| 11,56 | 2305,2 |
| 0,25 | 41,5 |
| 0,09 | 21,3 |
| 9,0 | 1767,0 |
| 16,81 | 3271,8 |
| 5,29 | 1085,6 |
| 0,64 | 130,4 |
| 1,69 | 319,8 |
| 0,64 | 174,4 |
| 0,16 | 37,6 |
| 4,00 | 870,0 |
| 7,84 | 1710,8 |
| 1,44 | 358,8 |
| 3,24 | 779,4 |
| 0,36 | 107,4 |
| 3,24 | 810,0 |
| 19,36 | 4743,2 |
| 8,41 | 1856,0 |
| 0,01 | 2,6 |
| 5,29 | 1030,4 |
| 10,24 | 2000,0 |
| 6,76 | 1211,6 |
| 0,85 | 156,4 |
Продолжение таблицы 10
| 1 | 2 |
| 7,95 | 1393,1 |
| 0,49 | 95,2 |
| 0,25 | 45,0 |
| 0,81 | 123,3 |
| 0,16 | 20,4 |
| 2,56 | 427,2 |
| 1,96 | 329,0 |
| 0,09 | 11,7 |
| 0,25 | 29,5 |
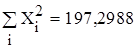
| 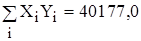
|
Значение а0 определяем из первого уравнения :
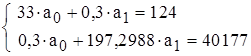
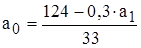 , или
, или 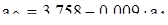 .
.
Подставляя найденное выражение 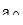 во второе уравнение, находим
во второе уравнение, находим 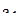 :
:
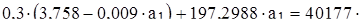 а1;
а1;
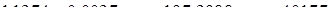 ;
;
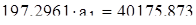 ;
;
 ;
;
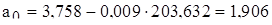 .
.
Итак, уравнение регрессии в окончательном виде получило следующий вид:
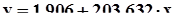
Графики полученных уравнений приведены на рисунке 10.
Рисунок 10 – Зависимость изменения объема СМР от изменения
численности рабочих и изменения выработки (по СМУ-21)
Анализ зависимости объема работ от численности
рабочих по ЖБК-2
Имеем фактические данные об изменении объема выполнения работ и изменении численности рабочих по ЖБК-2 (таблица 11). (Последующие расчеты аналогичны предыдущим и выполнены при помощи ЭВМ).
Таблица 11 – Фактические данные об изменении объема выполнения работ и изменении численности рабочих
Изменение численности рабочих,
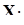
| Изменение объема выполнения работ,
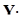
|
| +28 | +365,63 |
| +23 | +150 |
| +34 | +997 |
| +5 | +279,93 |
| -3 | -209 |
| -2 | -53 |
| 0 | +115 |
| +11 | +139 |
| -6 | -265 |
| -14 | -181 |
| -1 | -220 |
| -11 | -264 |
| +31 | +832 |
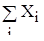 =+95 =+95
| 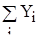 =+1686,56 =+1686,56
|
В ходе анализа получаем следующее уравнение регрессии:
y=-32,135+21,151 x
при коэффициенте корреляции, равном 0,892.
Анализ зависимости объема работ от выработки
одного рабочего по ЖБК-2
Имеем фактические данные об изменении объемов выполнения и изменении выработки на 1 рабочего ППП (таблица 12).
Таблица 12 – Фактические данные об изменении объемов выполнения работ и изменении выработки 1 рабочего
Изменение выработки 1 рабочего,
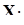
| Изменение объема выполнения работ,
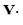
|
| 1 | 2 |
| +0,9 | +250,3 |
| +0,4 | +1128,0 |
| -1,1 | -1527,5 |
| +0,4 | +115,0 |
| +0,2 | +89,0 |
| -1,8 | -970,0 |
| -0,7 | -265,0 |
| -1,4 | -627,0 |
| -1,8 | -547,0 |
| -3,0 | -1435,0 |
| +1,7 | +1513,0 |
| -1,6 | -939,0 |
| +1,7 | +884,0 |
| -2,1 | -933,0 |
| +0,5 | +183,0 |
| +0,68 | +535,0 |
| +0,92 | +412,0 |
| +0,6 | +17,0 |
Продолжение таблицы 12
| 1 | 2 |
| -0,6 | -264,0 |
| +1,0 | +477,0 |
| -1,9 | -1117,0 |
| +1,4 | +1181,0 |
| +1,2 | +832,0 |
| -1,7 | -1170,0 |
| +1,8 | +1254,0 |
| -2,2 | -1563,0 |
| +1,1 | +1082,0 |
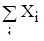 =-5,40 =-5,40
| 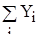 =-1405,23 =-1405,23
|
При проведении анализа получаем следующее уравнение регрессии:
y=95,745+552,841 x,
при коэффициенте корреляции равном 0,889.
Графики полученных уравнений приведены на рисунке 11.
Таким образом, в ходе проведенных исследований можно сделать прийти к заключению, что управление АК "Домостроитель" довольно эффективно за счет того, что переделы "Изготовление" и "Монтаж" находятся "в одних руках". Потери же во времени возникают в результате того, что работа с контрактами ведется "по старинке". При заключении договоров не учитываются факторы, оказывающие влияние на сроки строительства. Так как можно оказывать влияние только на внутренние факторы, то именно для них в ходе работы и выявлены следующие зависимости.
Рисунок 11 – Зависимость изменения объема СМР от изменения
численности рабочих и изменения выработки (по ЖБК-2)
ЖБК-2.
Зависимость объема работ от численности рабочих:
y=-32,135+21,151 x
Зависимость объема работ от выработки одного рабочего:
y=95,745+552,841 x,
СМУ-21.
Зависимость объема работ от численности рабочих:
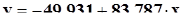
Зависимость объема работ от выработки одного рабочего:
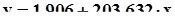
ВЫВОДЫ И РЕКОМЕНДАЦИИ
По проведении исследований можно дать рекомендации по следующим направлениям.
Рекомендации о порядке заключения и исполнения договоров.
Дата: 2019-07-24, просмотров: 318.