Теперь физики увидели атом как небольшое, но обладающее большой массой атомное ядро, окруженное электронами. Поскольку практически всю массу атома составляет ядро, то с увеличением атомного веса должна увеличиваться и масса ядра.
Логично предположить, что чем больше масса атомного ядра, тем выше его положительный заряд и тем больше электронов необходимо для того, чтобы заряд всего атома оставался нейтральным. А раз так, то постепенно становится ясным, в чем заключается различие между атомами различных химических элементов, и различие это вовсе не в массе, как считал Дальтон и остальные ученые XIX века. Различие имеет совершенно новую, электрическую природу. Атомы различных химических элементов отличаются зарядом ядра атома и количеством электронов за пределами ядра.
Эти два аспекта электрического различия атомов тесно связаны между собой, однако заряд — величина более постоянная, чем количество электронов. Под действием света и тепла электроны могут покинуть атом, превратив его в положительно заряженный ион, а появление в атоме дополнительных электронов приводит к образованию отрицательно заряженного иона. Несмотря на то что свойства иона разительно отличаются от свойств атома, от которого он образован, все-таки ион не является новым элементом. Другими словами, даже несмотря на то, что ион натрия по свойствам сильно отличается от атома натрия, даже физики и химики XIX века могли легко превратить его обратно в атом натрия, и хотя превратить ион калия в атом калия и наоборот они уже не могли, но в принципе это возможно. Значит, количество электронов не является ключевым отличием атома одного элемента от атома другого.
А вот изменить заряд ядра атома ученые того времени не могли. Заряд ядра атома остается постоянным независимо от количества электронов. Таким образом, все разнообразие атомов и соответственно химических элементов удобнее всего характеризовать по разности зарядов их атомных ядер.
Но как определить точную величину заряда атомного ядра? Ответ подсказали рентгеновские лучи.
Рентген получил свои лучи, направив катодный луч на стекло стенки катодной трубки. Электроны, проникая сквозь какой-либо объект, замедляются, и при достаточной толщине объекта они могут остановиться полностью. Согласно теории электромагнетизма Максвелла понижение скорости заряженных частиц приводит к возникновению электромагнитного излучения, в данном случае — рентгеновских лучей.
Понятно, что вещество, состоящее из более тяжелых атомов, будет эффективнее задерживать электроны, а рентгеновское излучение будет более интенсивным. Именно поэтому физики стали помещать металлическую пластину внутри катодной трубки непосредственно перед катодом. Электроны, попадая на эту пластину — антикатод («напротив катода»), тормозятся, и появляется мощное рентгеновское излучение. Такая трубка получила название рентгеновская.
В 1911 году английский физик Чарлз Баркла (1877–1944) обнаружил, что свойства получаемых рентгеновских лучей зависели от материала, из которого сделан антикатод, то есть определенный материал производил определенные группы лучей. Баркла мог судить о различиях этих групп лишь по их проникающей способности. Лучи одной группы могли проходить сквозь толстый материал, другой — сквозь более тонкие и т. д. Чем жестче рентгеновский луч, тем выше его проникающая способность. Впоследствии самые жесткие лучи стали называть лучами группы К, менее жесткие — группы L, М и т. д. Определенные материалы производят определенное, т. е. уникальное рентгеновское, излучение.
Жесткость лучей уникального излучения зависит от металла, из которого сделан антикатод. Чем выше атомный вес металла, тем «тверже» производимые им рентгеновские лучи. Стало очевидным, что если точно измерить их «твердость», то можно узнать много интересного об атомном ядре.
К сожалению, результаты измерения жесткости рентгеновских лучей по их проникающей способности были весьма приблизительными, нужно было что-то более точное. Ученые давно предполагали, что рентгеновские лучи являются частным случаем электромагнитного излучения (впрочем, когда Баркла анализировал результаты своих экспериментов, это еще не было доказано). Если это так, тогда чем короче длина рентгеновского луча, тем выше его энергия и проникающая способность. Таким образом, измерения длины волны (т. е. частоты) рентгеновских лучей дают возможность точно определить степень их жесткости.
Но как измерить длину волны? По идее для этого нужно использовать дифракционную решетку (см. ч. II). Дифракционная решетка — это экран с большим количеством параллельных щелей. Ширина щелей должна быть равна длине измеряемой волны. Длина рентгеновского луча намного меньше длины ультрафиолетового излучения, поэтому создать такую решетку практически невозможно.
В 1912 году немецкий физик Макс Лауэ (1879–1960) предложил для измерения длины волны рентгеновского излучения использовать кристаллы. Структура кристалла представляет собой расположенные рядами атомы, иначе говоря, кристалл является естественной дифракционной решеткой. Ни одна дифракционная решетка, созданная человеком, не обладает столь малой шириной щелей.
Расстояние между атомными ядрами, которые и будут разлагать пучки рентгеновских лучей в спектр так же, как щели обычной дифракционной решетки разлагают в спектр обычный свет, составляет около 10–8 см, что приблизительно и равно длине волны рентгеновского луча.
В опытах Лауэ пучок рентгеновских лучей, проходя сквозь кристалл сульфида цинка, падал на фотопластинку, оставляя вместо четкого отпечатка узор из нескольких точек. Значит, дифракция рентгеновских лучей действительно имела место, что и послужило доказательством волновой природы рентгеновского излучения.
В том же году два английских физика, Уильям Генри Брэгг и его сын, Уильям Лоренс Брэгг, развили идею Лауэ. Проанализировав поведение проходящих через кристалл рентгеновских лучей, они пришли к выводу, что угол отклонения лучей зависит от расстояния между атомами кристалла и от длины волны. Зная расстояние между атомами, можно определить длину волны.
Метод позволял высчитать длину волны рентгеновского луча с достаточной точностью. Спектр рентгеновского излучения, появляющегося при столкновении электронов с преградой, колеблется от 1 (нижняя граница диапазона ультрафиолетового излучения) до 0,01 миллимикрона (7 октав).
Атомные числа
Использование метода Брэгга давало возможность изучить уникальные рентгеновские излучения, о которых говорил Баркла, что и было сделано в 1913 году английским физиком Генри Гвином Джефрисом Мозли (1997–1915).
Мозли изучал рентгеновские лучи группы К применительно к 12 следующим друг за другом элементам периодической системы и обнаружил, что длина волны уменьшалась (то есть частота повышалась) с увеличением атомного веса, причем квадратный корень длины волны увеличивался пошагово.
Мозли предположил, что причиной этому является пошаговое увеличение заряда ядра атома. Ученый пришел к выводу, что ядро простейшего атома несет заряд +1, заряд следующего +2, еще следующего +3 и т. д. Мозли назвал величину этого заряда атомным числом.
Ученый оказался прав. Сегодня за атомный вес водорода принято число 1, гелия — 2, лития — 3 и т. д. В настоящее время определены атомные числа всех известных элементов. В табл. 3 элементы представлены в порядке увеличения их атомных чисел от 1 до 103.
Для периодической системы атомные числа имеют гораздо более важное значение, чем атомные веса. Для того чтобы в таблице все элементы одного семейства были на своих местах, Менделееву пришлось поставить некоторые более тяжелые элементы перед более легкими. Так, кобальт с атомным весом 58,93 стоит перед никелем с атомным весом 58,71.
Мозли выяснил, что кобальт, несмотря на больший атомный вес, производит рентгеновские лучи более низкой, чем никель, частоты. Поэтому и атомное число у кобальта (27) меньше, чем у никеля (28). Хотя Менделееву ничего не было известно о рентгеновских лучах, интуиция химика не подвела его.
Таким образом, если рассматривать те пары элементов, что стоят в периодической системе не по порядку возрастания их атомных весов (аргон — калий, кобальт — никель, теллур — йод), а с точки зрения возрастания атомных чисел, то все становится на свои места.
Кроме того, благодаря открытию атомных чисел у периодической таблицы появляется еще одно свойство. Теперь с ее помощью можно не только предсказывать существование пока еще неизвестных элементов (что Менделеев и сделал), но и их несуществование.
Пока на вооружении ученых были лишь атомные веса, нельзя было сказать наверняка, что в будущем не будут открыты целые семейства новых элементов. Например, в 1890 году было открыто семейство инертных газов (гелий, неон, аргон, криптон и ксенон), и в таблицу тут же добавили новую колонку, ранее о существовании которой даже и не подозревали. Столетие спустя были открыты лантаноиды, и их тоже включили в таблицу. До Мозли никто не мог точно сказать, сколько еще оставалось неизвестных элементов. Десятки? Сотни? Тысячи?
Атомные числа не оставили места для подобных сомнений. Подразумевая, что атомное ядро не может нести дробный заряд, можно с уверенностью заявить, что между водородом (атомное число 1) и гелием (2) или, скажем, фосфором (15) и серой (16) никаких элементов нет.
Впервые химики могли сказать, сколько еще элементов предстояло открыть. Первым элементом в таблице является водород (атомное число 1), других элементов перед ним нет. Во времена Мозли самым тяжелым из известных элементов был уран (92). Между ними были лишь 7 неизвестных элементов с атомными числами 43, 91, 72, 75, 85, 87 и 91.
Рентгенографический анализ можно также использовать для проверки новых элементов. Например, в 1911 году французский химик Жорж Урбен (1872–1938) выделил, как ему показалось, новый элемент и дал ему название «кельтий». Когда Мозли опубликовал свой труд, Урбен решил, что кельтий — это как раз и есть неизвестный элемент с атомным числом 72, и привез образец на проверку к Мозли. Проанализировав уникальное рентгеновское излучение «нового» элемента, Мозли выяснил, что кельтий был на самом деле смесью двух уже известных элементов — иттербия и лютеция (атомные числа 70 и 71). Химические испытания это подтвердили, и потрясенный увиденным Урбен впоследствии сделал много для популяризации концепции атомных чисел.
В течение последующих 12 лет были заполнены 3 пустые клетки таблицы. В 1917 году был открыт протактиний (91), в 1923 году — гафний (72), в 1925 году — рений (75). Еще через 10 лет были заполнены оставшиеся четыре клетки (43, 61, 85, 87). Эти элементы мы рассмотрим ниже.
Зная заряд ядра атома элемента, можно судить и о количестве электронов в атоме. Конечно же атом может потерять или присоединить электроны и превратиться в положительно или отрицательно заряженный ион, но в атоме с нейтральным зарядом количество электронов должно соответствовать заряду ядра. Так, в атоме кислорода с зарядом ядра +18, для того чтобы заряд атома оставался нейтральным, должно присутствовать 18 электронов. То есть количество электронов в атоме равно атомному числу этого элемента. Таким образом, у атома водорода один электрон, у натрия — 11, а у урана — 92.
Электронные оболочки
Теперь возник еще один вопрос: как все эти электроны расположены в атоме? Томсон с его моделью атома в виде булочки с изюмом предположил, что электроны внутри атома расположены по кругам. Чем больше электронов — тем больше кругов.
И хотя модель атома Томсона и была вытеснена моделью атома с ядром Резерфорда, идея о том, что электроны находятся за пределами ядра, казалась вполне вероятной, а существование уникального рентгеновского излучения лишь подтверждало ее. Возможно, что каждая из групп лучей испускалась определенной группой электронов вокруг ядра. Электроны, находящиеся в непосредственной близости от ядра, удерживаются им сильнее, значит, они и производят самое жесткое излучение группы К. Электроны, находящиеся чуть дальше от ядра, будут производить излучения группы L и т. д. Приведенный ниже рисунок наглядно это иллюстрирует.
А почему, например, благородные газы (гелий, неон, аргон, криптон, ксенон и радон) практически не вступают в химические реакции? (На самом деле долгое время считалось, что они вообще ни с чем не реагируют, и только в 1962 году выяснилось, что с некоторыми элементами они все же реагируют.)
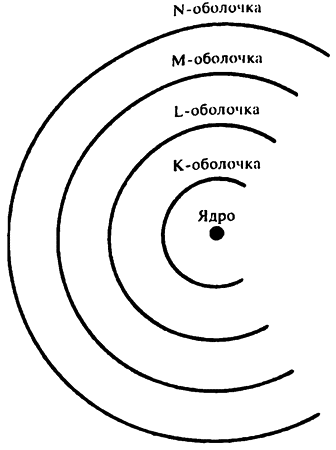
Электронные оболочки
Одной из причин является то, что любая химическая реакция включает в себя в том числе и взаимодействие электронов внутри атомов. Например, хлорид натрия состоит из ионов натрия и газообразного хлора. В процессе реакции атом натрия теряет один электрон и становится положительно заряженным ионом Na+, а атом хлора присоединяет один электрон и становится отрицательно заряженным ионом Cl–.
Возможно, благородные газы не вступают в химические реакции потому, что уже обладают жесткой электронной структурой, а присоединение или потеря электронов приведет к потере этой структурной устойчивости.
Логично предположить, что эта устойчивость достигается полным заполнением одной из электронных оболочек.
Например, атомное число гелия равно 2, и гелий является благородным газом. Если атом гелия содержит два электрона, значит, ему необходимы лишь два электрона для полного заполнения внутренней электронной оболочки К. Атом следующего благородного газа — неона — в нейтральном состоянии обладает 10 электронами, 2 из которых заполняют оболочку К, а оставшиеся 8 — оболочку L. В каждом атоме аргона (атомное число 18) уже по 18 электронов, 2 из которых заполняют оболочку К, еще 8 — L, а оставшиеся 8 — оболочку М. В табл. 4 показано, как электроны по электронным оболочкам распределены у первых 20 элементов. (У элементов с большим атомным числом распределение становится уже более сложным, см. гл. 5.)
Вскоре после опубликования Мозли своих работ были сделаны первые попытки рассмотреть химические реакции с точки зрения распределения электронов по электронным оболочкам. Успехом увенчались попытки работавших независимо друг от друга американских химиков Гилберта Ньютона Льюиса (1875–1946) и Ирвинга Ленгмюра (1881–1957). Суть их теории вкратце заключается в том, что в процессе любой химической реакции элементы стараются потерять или присоединить электроны, чтобы перейти в такое же, как и у благородных газов, устойчивое состояние.
Так, натрий с распределением электронов по оболочкам 2/8/1 проявляет тенденцию отдать один электрон, чтобы превратиться в ион натрия (Na+) с распределением электронов 2/8, как у атома неона. Конечно же ион натрия не превращается в атом неона, так как заряд ядра (уникальный для каждого элемента) иона натрия остается +11, а заряд ядра атома неона равняется +10. То же можно сказать и о хлоре. Атом хлора с распределением электронов 2/8/7 проявляет тенденцию присоединить еще один электрон и стать ионом хлора (Cl–) с распределением электронов 2/8/8, как у атома аргона.
Легкость, с которой натрий и хлор реагируют друг с другом, объясняется их обоюдным желанием отдать и присоединить электрон. Атом хлора присоединяет «лишний» электрон натрия, после чего элементы превращаются в ионы с разноименным зарядом и притягиваются друг к другу.
Точно так же кальций (2/8/8/2) легко отдает 2 электрона и становится ионом кальция (Са++) с распределением электронов по аргону (2/8/8), а кислород (2/6) присоединяет эти 2 электрона и становится оксид-ионом (О––) с распределением по неону (2/8). Вместе эти ионы образуют оксид кальция (СаО).
Или кальций может отдать один электрон одному атому хлора, а второй — другому, и тогда образуется хлорид кальция (СаСl2), то есть один грамм-атом хлора соединяется с половиной грамм-атома кальция. Таким образом, с точки зрения электронов можно объяснить существование эквивалентных масс.
Таблица 4.
РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ
ЭлементАтомное числоЧисло электронов в оболочкеКLМNВодород11___Гелий22——_Литий321—_Бериллий422——Бор523——Углерод624——Азот725__Кислород826——Фтор927——Неон1028——Натрий11281—Магний12282—Алюминий13283—Кремний14284—Фосфор15285—Сера16286—Хлор17287—Аргон18288—Калий192881Кальций202882Но как же тогда образуется молекула хлора? Ведь атом хлора проявляет тенденцию присоединить, но никак не отдать электрон. Льюис и Ленгмюр предположили, что если два атома хлора находятся в непосредственной близости, то их внешние электронные оболочки соприкасаются и заполняются электронами друг друга, и общее число электронов каждого атома становится таким же, как и аргона, — 2/8/8.
Понятно, что любая попытка удалить атомы хлора друг от друга ставит под угрозу существование общей электронной оболочки, и именно поэтому молекула хлора чрезвычайно устойчива. Для разложения ее на отдельные атомы необходимо достаточно большое количество энергии.
По той же причине молекулы фтора, водорода, кислорода и азота также состоят из двух атомов.
Распределение атомов внутри атома углерода — 2/4. Значит, один атом углерода может образовать общие электронные оболочки с четырьмя атомами водорода. Таким образом, с помощью четырех атомов водорода атом углерода заполняет внешнюю электронную оболочку по неону (2/8), как у атома неона, каждый атом водорода с помощью одного атома углерода заполняет свою электронную оболочку по гелию (2), а молекула метана (СН4) становится устойчивой.
Действительно, теория Льюиса — Ленгмюра о переходящих и общих электронах объясняет, как образуются молекулы большинства простейших химических соединений. Более того, эта теория объясняет, почему периодическая таблица и является, собственно говоря, периодической (сам Менделеев конечно же не мог этого объяснить). Начнем с того, что в атомах благородных газов электроны распределены таким образом, чтобы придавать атомам максимальную устойчивость. Благородные газы являются инертными химическими веществами и выделяются в отдельное семейство обладающих естественной устойчивостью и очень похожих друг на друга элементов.
Каждый из щелочных металлов следует за одним из инертных газов, следовательно, их атомное число на единицу больше, чем у одного из инертных газов. У лития (следующий за гелием) электроны распределены как 2/1; у натрия (следующий за неоном) — 2/8/1; у калия (следующий за аргоном) — 2/8/8/1 и т. д. У каждого из щелочных металлов на внешней оболочке по одному электрону, и все они проявляют тенденцию отдать его для приобретения естественной устойчивости.
У каждого из образующих щелочноземельное семейство металлов по 2 электрона на внешней оболочке: 2/2 у бериллия, 2/8/2 у магния, 2/8/8/2 у кальция и т. д.
Атомное число галогенов на единицу меньше, чем у благородных газов: 2/7 у фтора, 2/8/7 у хлора и т. д. Все элементы этого семейства проявляют тенденцию присоединить один электрон для достижения естественной устойчивости.
Таким образом, с помощью электронов и электронных оболочек периодическая таблица получила наконец рациональное объяснение спустя полвека после своего появления.
Глава 5.
ЭЛЕКТРОНЫ И КВАНТЫ
Спектральный ряд
Однако как ни хороша теория Льюиса — Ленгмюра, она объясняет структуру лишь простейших химических соединений. С ее помощью невозможно объяснить, например, структуру гидрида бора (соединения бора и водорода) или свойства бензола (С6Н6). Также невозможно объяснить и поведение элементов с атомными числами меньше, чем у кальция, или почему так схожи свойства лантаноидов, хотя их атомные числа разнятся от 57 до 71.
Слабым местом во взглядах Льюиса и Ленгмюра является то, что ученые рассматривали электроны как неподвижные частицы, занимающие внутри атома строго определенные места. Действительно, на рисунках того времени электроны оболочек L и М располагались по восьми углам куба, а молекулы простейших соединений состояли из нескольких таких кубов, соединенных вместе.
Конечно же такое представление удобно с химической точки зрения, но абсолютно неприемлемо с физической. Ведь если отрицательно заряженный электрон висит над положительно заряженным ядром неподвижно, то он должен просто-напросто упасть на ядро. (Точно так же Земля упала бы на Солнце, если бы не вращалась вокруг него.)
Постепенно физики пришли к выводу, что электрон, чтобы не упасть на ядро, вращается вокруг него с огромной скоростью. В 1904 году японский физик Хантаро Нагаока предположил, в частности, что электроны движутся вокруг ядра так же, как планеты движутся по своим орбитам вокруг Солнца[123].
Впрочем, все модели атомов, где электроны вращались вокруг ядра, сталкивались с одной и той же проблемой. Вращающийся вокруг ядра электрон постоянно испытывает центростремительное ускорение, а согласно теории Максвелла постоянно ускоряющийся заряд должен постоянно испускать электромагнитное излучение.
Именно такую модель и создал Нагаока. Электрон, двигающийся вокруг ядра, и является этим зарядом и должен испускать излучение определенной частоты (как и в случае с искрами у Герца, см. гл. 2). Если электрон в минуту совершает 500 триллионов оборотов вокруг ядра (а это всего лишь 150 километров в секунду), то частота его излучения будет 500 триллионов Гц, а это в пределах видимой части спектра, ведь свет — это тоже электромагнитное излучение.
Предположение, конечно, красивое, но разрушить его все-таки придется. Если вращающийся электрон будет испускать излучение постоянно, то он будет терять энергию, а единственной энергией, которой обладает электрон, является кинетическая (т. е. энергия движения). Соответственно движение электрона вокруг ядра должно постепенно замедляться, а сам электрон будет по спирали приближаться к ядру, пока не остановится окончательно и не притянется ядром[124].
Но раз электроны на ядро не падают, нужно создавать какую-то другую модель. Новая модель должна отражать тот факт, что атомы не только излучают (и поглощают) свет, но излучают и поглощают свет лишь определенной частоты. Для создания модели атома следует изучить взаимосвязи между этими уникальными световыми волнами, а отталкиваться нужно от водорода, поскольку водород излучает волны самого простого и упорядоченного спектра.
Длина волн, образующих самые четкие линии спектра водорода, составляет 656,21 миллимикрона, 486,08 миллимикрона, 434,01 миллимикрона, 396,81 миллимикрона и так далее. Расстояние между линиями уменьшается пошагово, значит, здесь определенно должна быть какая-то закономерность.
В 1885 году немецкий математик Иоганн Якоб Бальмер (1825–1898) вывел простую формулу, по которой можно рассчитать длину этих волн:
λ = 364,56m2/(m2 – 4), (Уравнение 5.1)
где m может быть любым целым числом начиная с 3. Если m = 3, то λ будет равна 656,21 миллимикрона, т. е. длине первой волны водородного спектра. Если подставлять вместо m числа 4, 5, 6, то λ будет равна длине второй, третьей и четвертой линии водородного спектра. Эти линии получили название серия Бальмера.
С возрастанием значения m значение m2 − 4 знаменателя будет практически равно значению m2 числителя, и дробь сократится. В этом случае λ будет равно 364,56 миллимикрона (постоянная Бальмера). Именно к этому значению длины волны стремятся все линии серии Бальмера.
Через несколько лет шведский физик Юханнес Роберт Ридберг (1854–1919), преобразовав формулу Бальмера, сделал ее более удобной. Сначала он написал возвратное уравнение:
1/λ = (m2 – 4)/(364,56m2). (Уравнение 5.2)
Затем, умножив знаменатель и числитель дроби в правой части формулы 5.2 на 4, получил:
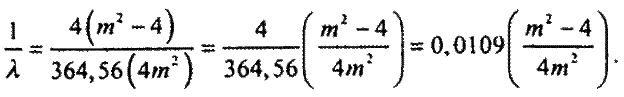
Давайте рассмотрим каждый член правой части формулы 5.3 по отдельности. Число 0,0109 получается делением 4 на бальмерову константу. Это значение в миллимикронах. Ридберг предпочел использовать сантиметры, а раз в одном сантиметре 10 000 000 миллимикрон, то значение в сантиметрах будет 0,0109∙10 000 000 = 109 (современные измерения дают значение 109 737 31). Это число получило название постоянная Ридберга и обозначается как R. Таким образом, в пересчете на сантиметры формула 5.3 будет выглядеть так:
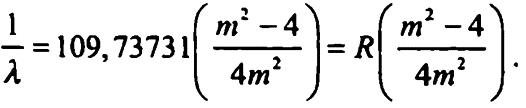
Получаем значение λ в сантиметрах, т. е. длина основной волны равна 0,000065621 см.
Теперь разложим (m2 – 4)/4m2 на m2/4m2 – 4/4m2 и сократим до 1/4 — 1/m2. Для симметрии представим 4 как 1/22 – 1/m2, тогда формула 5.4 приобретает вид:
1/λ = R∙(1/22 - 1/m2), (Уравнение 5.5)
где m — любое целое число, равное и большее 3.
Формулы оставшихся линий будут выглядеть аналогично:
1/λ = R∙(1/12 - 1/m2), (Уравнение 5.6)
1/λ = R∙(1/32 - 1/m2), (Уравнение 5.7)
1/λ = R∙(1/42 - 1/m2) (Уравнение 5.8)
и так далее. Значением m для формулы 5.6 должно быть любое целое число больше 1, для формулы 5.7 — больше 3, для формулы 5.8 — больше 4.
Формула 5.6 описывает волны ультрафиолетового спектра. Эти волны короче волн серии Бальмера. Они были открыты в 1906 году американским физиком Теодором Лайманом и получили название волны серии Лаймана.
Формула 5.7 описывает волны инфракрасного спектра. Они длиннее волн серии Бальмера. Они были открыты в 1908 году немецким физиком Фридрихом Пашеном и получили название серия Пашена. Формула 5.8 описывает еще более длинные волны, открытые американским физиком Фредериком Брэкеттом и получившие названия серия Брэкетта. Существуют также и другие серии волн.
Атом Бора
Итак, электроны атома водорода не только не падают на ядро, но еще и испускают волны определенной частоты, которые можно определить по простым формулам Ридберга. Нужна была новая модель атома, которая бы все это отражала.
Такую модель создал в 1913 году датский физик Нильс Бор (1885–1962). Он предложил использовать для решения задачи только в то время появившуюся квантовую теорию (см. ч. II).
Согласно квантовой теории, любой преобразовывающий кинетическую энергию в излучение объект теряет эту энергию. Так, например, Земля постепенно теряет кинетическую энергию за счет вращения вокруг Солнца, однако эти потери настолько малы, что даже самые точные измерения не смогут зафиксировать какое-либо изменение в скорости вращения планеты.
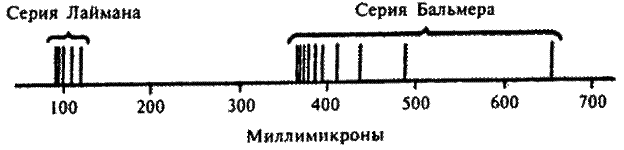
Спектр водорода
Но с электронами дело обстоит иначе. Общая кинетическая энергия электрона немного превышает энергию одного кванта видимого света, то есть для излучения одного кванта света электрону потребуется мгновенно потратить всю свою энергию. Однако вместо того, чтобы медленно приближаться к ядру во время вращения (как это себе представляли физики «доквантовой» эры), электрон просто «перепрыгнет» на более близкую к ядру орбиту. С другой стороны, если электрон также еще и поглощает свет, значит, он сразу поглотит целый квант света и на этот раз перепрыгнет уже на более высокую орбиту.
Бор предположил, что электрон в основном состоянии обладает минимумом энергии и находится на ближайшей к ядру орбите. Такой электрон не выделяет энергию (истинная причина этого открылась лишь 10 лет спустя, см. гл. 6). После поглощения энергии электрон переходит в возбужденное состояние и в зависимости от количества этой энергии занимает одну из более удаленных от ядра орбит.
Бор определил несколько орбит электрона в атоме водорода в зависимости от величины кинетического момента. Используя постоянную Планка (см. ч. II), Бор вывел следующую формулу:
p = nh/2π , (Уравнение 5.9)
где p — кинетический момент электрона, h — постоянная Планка, π — это конечно же известная нам постоянная длины окружности; n — любое положительное целое. Теперь введем в формулу значение постоянной Планка, предположим, что электрон может двигаться только по определенным орбитам, примем за n любое целое число и получим квантованный атом.
В связанных с квантованным атомом вычислениях выражение h/2π используется часто, поэтому его обычно сокращают до ħ. Так как значение h приблизительно 6,6256∙10–27 эрг-с, значение π приблизительно 3,14159, то ħ приблизительно равно 1,0545∙10–27 эрг-с.
Таким образом, формула 5.9 приобретает вид:
p = n (1,0545∙10–27). (Уравнение 5.10)
Иногда n называют еще главным квантовым числом (кроме главного, существуют и другие квантовые числа). Это число обозначает орбиту, на которой находится электрон: n = 1 для ближайшей к ядру орбите; 2, 3, 4 и так далее — для более высоких.
Когда единственный электрон атома водорода опускается с орбиты 2 на орбиту 1, он выделяет один квант (определенного размера) энергии, т. е. излучение определенной частоты, и в определенном месте спектра появится яркая линия. (А когда единственный электрон атома водорода поднимается с орбиты 1 на орбиту 2, он поглощает один квант (того же определенного размера), и на месте яркой спектральной линии появится еще и темная.)
Если единственный электрон атома водорода опустится с орбиты 3 на орбиту 1, то энергии при этом выделится больше, и частота излучаемого света будет выше. При перемещении с орбиты 3 (4, 5) на орбиту 1 частота будет еще выше.
Серия перемещений с различных орбит на орбиту 1 приведет к излучению света последовательно повышающейся частоты (или последовательно понижающейся длины волны), то есть серии волн Лаймана. Серия перемещений с более высоких орбит на орбиту 2 приведет к появлению серии Бальмера, на орбиту 3 — серии Пашена и т. д.
В описывающих длины волн спектральных линий различных серий формулах (5.5, 5.6, 5.7, 5.8) первое число знаменателя правой части и будет главным квантовым числом орбиты, куда опускается (или с которой поднимается) электрон.
Заряд ядра атомов более сложной, чем у водорода, структуры с несколькими электронами больше, следовательно, электроны на внутренней орбите удерживаются сильнее.
Поэтому для перемещения на более высокую орбиту электрону требуется больше энергии, а значит, и при переходе на более низкую орбиту энергии также освобождается больше. Самые короткие излучаемые водородом волны находятся в ультрафиолетовой части спектра (серия Лаймана), а более сложные атомы могут излучать и сверхкороткие рентгеновские лучи. Мозель обнаружил, что длина волн рентгеновского излучения уменьшается с возрастанием атомного числа элемента.
Дальше — хуже. Модель атома Бора вполне подходила для атомов водорода, чей спектр состоит из прямых линий. Однако более точный спектральный анализ показал, что спектральные линии водорода имеют тонкую структуру, состоящую из многих мелких линий, будто электрон при перемещении на другую орбиту «промахивается» и попадает на соседнюю.

Атом Бора
Это едва не поставило крест на квантовой модели атома. Положение спас в 1916 году немецкий физик Арнольд Зоммерфельд (1868–1951), предложивший следующее объяснение: дело в том, что, по мнению Бора, электронные орбиты имели четкую форму круга, однако Зоммерфельд предположил, что она может быть и эллиптической. Квантовая модель атома допускала существование орбит с небольшим эксцентриситетом эллипса, а главное квантовое число — группы орбит, состоящих из одной круговой и нескольких эллиптических, так как изменения кинетического момента были незначительными.
Для эллиптических орбит Зоммерфельд ввел понятие орбитального квантового числа, получившего обозначение L[125] . Орбитальное квантовое число может принимать любое значение в пределах от 0 до n – 1, то есть при n = 1 L = 0; при n = 2 L = 0 или 1; при n = 3 L = 0, 1 или 2 и т. д.
Но спектральные линии под действием магнитного поля расходятся еще больше. Ученые приняли это во внимание и ввели магнитное квантовое число (m).
С появлением магнитного атомного числа атом стали рассматривать уже в трех измерениях. Теперь варьировалась не только форма орбиты электрона, но и ее наклон относительно основной. Для т справедливы все значения L, кроме того, к положительным значениям добавились еще и отрицательные. То есть если для n = 2 L = 1 или 0, а m = 0, 1 и –1; для n = 3 L = 0, 1 или 2, а m = 0, 1, 2, –1 или –2 и т. д.
Последнее квантовое число — число спина электрона (s). Оно обозначает спин, т. е. направление вращения электрона вокруг своей оси, а поскольку таких направлений всего два — по часовой стрелке и против часовой, то и квантовое число может принимать лишь два значения: 1/2 и –1/2.
Электронные подоболочки
Электроны могут находиться лишь на описанных квантовыми числами орбитах. Когда электронов несколько (а у всех элементов, кроме водорода, их по два и более), они распределяются по орбитам, причем первой заполняется ближняя к ядру орбита.
Но сколько электронов могут находиться на одной и той же орбите одновременно? В 1925 году австрийский физик Вольфганг Паули (1900–1958) предположил, что, раз спектр каждого элемента уникален, значит, внутри каждого атома не могут существовать электроны с идентичными квантовыми числами, хотя бы одно из четырех должно отличаться. То есть на произвольной орбите, будь то круговая, эллиптическая или накрененная, могут вращаться максимум 2 электрона, причем один из них по часовой стрелке, а второй — против. Этот принцип существования двух электронов с противоположными спинами называется принцип исключения Паули.
Теперь мы можем определить количество электронов на каждой представленной соответствующим квантовым числом группе орбит.
Пусть n = 1, тогда L = 0 и m = 0, т. е. характеристики единственной орбиты — 1/0/0. На такой орбите могут находиться два электрона с противоположными спинами. Общим числом электронов первой группы орбит (n = 1) является 2.
Теперь предположим, что n = 2, тогда L = 0 или 1, а m = 0,1 или –1; при L = 0 и m = 0. Тогда для n — 2 существуют 4 возможные орбиты; 2/0/0; 2/1/0; 2/1/1 и 2/1/–1. На каждой из этих орбит могут находиться по два электрона с противоположными спинами, следовательно, общее число электронов второй группы орбит — 8.
Таким же образом можно определить, что общее число электронов следующей группы орбит (n = 3) равняется 18. То есть максимальное количество электронов группы орбит n можно вычислить по формуле 2n2. Отсюда для группы орбит 4 (n = 4) общим числом электронов является 32, для n = 5–50 и т. д.
В физике группы орбит, представленные главным квантовым числом л, соответствуют электронным оболочкам в химии, представленным в модели атома Льюиса — Ленгмюра.
Общее количество электронов группы орбит можно согласно значению L разделить на подоболочки. Например, если n = 1, то L = 0, значит, первая электронная оболочка состоит всего лишь из одной подоболочки, где могут находиться 2 электрона.
Если п = 2, то L = 0 и 1. При L = 0 орбита всего одна (2/0/0), соответственно электронов максимум 2; но при L = 1 орбит уже 3 (2/1/0, 2/1/1, 2/1/–1) и максимальное количество электронов — 6. Итого на второй оболочке 8 электронов, составляющих две подоболочки: на одной 2 электрона, на второй — 6.
Точно так же 18 электронов третьей оболочки можно разделить на 3 подоболочки по 2, 6 и 8 электронов. Вообще электроны оболочки с главным квантовым числом n можно разделить на n подоболочек: первая подоболочка будет содержать 2 электрона, а каждая последующая — на 4 электрона больше, чем предыдущая (то есть 6, 10, 14, 18 и т. д.).
Эти подгруппы обозначаются латинскими s, p, d, f, g, h и /. To есть первая оболочка состоит из 1s подоболочки, вторая — из 2s и 2p подоболочек и т. д.
Теперь давайте попробуем применить все это собственно к химическим элементам. Первые два никаких трудностей не вызывают. У водорода 1 электрон, у гелия — 2, и все они находятся на единственной подоболочке первой электронной оболочки.
ЭлементКоличество электронов на 1s Атомное числоВодород 11Гелий22У всех элементов с атомным числом больше 2 на первой оболочке по 2 электрона. Оставшиеся электроны распределяются по внешним оболочкам. Следующие восемь элементов распределяют эти электроны на второй электронной оболочке, состоящей из 2s подоболочки (вмешает 2 электрона) и 2p подоболочки (вмещает 6 электронов).
ЭлементКоличество электронов наАтомное число1s2s2pЛитий21 3Бериллий22—4Бор2215Углерод2226Азот2237Кислород2248Фтор2259Неон22610У атома неона вторая электронная оболочка заполнена, и в атомах следующих элементов заполняется уже третья электронная оболочка. Эта оболочка состоит уже из 3 подоболочкек: 35 (2 электрона), Зр (6 электронов), 3d (до 10 электронов).
ЭлементКоличество электронов наАтомное число1s2s3s3p3d2рНатрий281——11Магний282——12Алюминий2821—13Кремний2822—14Фосфор2823—15Сера2824—16Хлор2825—17Аргон2826—18Обратите внимание на сходство заполнения оболочек этих элементов и элементов предыдущего списка. Одинаково заполнены 2s2р атома лития и 3s3p натрия; 2s2p бериллия и 3s3p магния; 2s2p бора и 3s3p алюминия и т. д. Вот почему таблица химических элементов является периодической.
У атома аргона на 3s и 3p подоболочках по 2 и 6 электронов соответственно — столько же, сколько и у неона на 2s и 2p. Оба этих элемента относятся к благородным газам. В то же время 3d подоболочка атома аргона не заполнена полностью — там есть место для 10 электронов. Значит, инертность благородных газов определяется полным заполнением s и p подоболочек внешней электронной оболочки их атомов, содержащих в общей сложности 8 электронов. Таким образом, наличие этого количества электронов на внешней оболочке является признаком благородного газа. Единственное исключение составляет гелий, у которого всего одна подоболочка (1s), которая также полностью заполнена.
Вы, возможно, предполагаете, что в атомах следующих за аргоном элементов заполнена подоболочка 3d. Однако это не так. Дело в том, что каждому электрону, условно говоря, требуется место, а каждая оболочка атома содержит все больше и больше электронных подоболочек, и в конце концов внешние подоболочки одной электронной оболочки начинают перекрывать внутренние подоболочки другой. В данном случае подоболочка 3d перекрывает подоболочку 45. To есть заполняется подоболочка 45, а не 3d.
ЭлементКоличество электронов наАтомное число1s2s3s3d4s2p 3p Калий 288—119Кальций288—220У кальция 1 электрон на подоболчке 4s, как у натрия на 3s и лития на 2s. Подобную аналогию можно провести между кальцием, магнием и бериллием.
Переходные элементы
Если бы у атома скандия, следующего за кальцием элемента, на 4р подоболочке был 1 электрон, то его s и р подоболочки были бы заполнены так же, как у алюминия (2 и 1 электрон). Этого, однако, не происходит. На 45 подоболочке атомов следующих за кальцием элементов 2 электрона (как у и кальция), а остальные электроны заполняют подоболочку 3d:
ЭлементКоличество электронов наАтомное число1s2s3s3d4s2p3pСкандий2881221Титан2882222Ванадий2883223Хром2885124Марганец2885225Железо2886226Кобальт2887227Никель2888228Медь28810129Цинк28810230Подоболочки 3d и 4s перекрывают друг друга достаточно нечетко, поэтому количество электронов на 3d/4s можно представить и как 5/1, и как 4/2, или, скажем, и как 10/1, и как 9/2. Впрочем, в случае с хромом и медью принято считать, что у них по одному электрону на 4s, ну да это не столь важно.
А важно то, что различия между этими десятью элементами (от скандия до цинка) заключаются в количестве электронов на подоболочке 3d, в то время как на внешней 4s подоболочке у всех (или почти у всех) количество электронов одинаково. Эти элементы называются переходными элементами. Они мало отличаются друг от друга по свойствам, в то время как разница между элементами от водорода до кальция (у которых по-разному заполняется именно внешняя подоболочка) очевидна.
Кобальт, железо и никель настолько похожи друг на друга, что ученые объединяют их в одно семейство элементов.
Однако модель атома Льюиса — Ленгмюра не допускает изменения количества электронов на внутренних оболочках и поэтому неприменима к переходным элементам, а ведь 3/5 всех элементов являются именно переходными.
У цинка третья электронная оболочка (18) и подоболочка 4s (6) заполнены полностью, поэтому в атомах элементов с большим атомным числом заполняется подоболочка 4p.
ЭлементКоличество электронов наАтомное число1s2s3s4s4p2p3p3dГаллий28182131Германий28182232Мышьяк28182333Селен28182434Бром28182535Криптон28182636У этих шести элементов подоболочки s и p заполнены так же, как у соответствующих элементов от алюминия до аргона и от бора до неона, поэтому галлий обладает свойствами, схожими с алюминием и бором, германий — с углеродом и кремнием и т. д. У криптона на 4s два электрона, а на 4p — 6 электронов, значит, криптон является благородным газом.
4d (10 электронов) и 4f (14 электронов) подоболочки четвертой электронной оболочки перекрывают внутреннюю 55 под-оболочку пятой электронной оболочки.
ЭлементКоличество электронов наАтомное число1s2s3s4s4d4f5s2p3p4p3dРубидий 28188——137Стронций28188— — 238У следующих элементов заполняется 4d подоболочка, значит, они так же, как и элементы от скандия до цинка, являются переходными.
ЭлементКоличество электронов наАтомное число1s2s3s4s4d4f5s2p3p4p3dИттрий281881— 239Цирконий281882—240Ниобий281884—141Молибден281885—142Технеций281885_243Рутений281887—144Родий281888—145Палладий2818810——46Серебро2818810—147Кадмий2818810— 248У следующих шести элементов заполняется 5p подоболочка, они не являются переходными, а соотношение электронов на s и p у них такое же, как и группы элементов от бора до неона.
ЭлементКоличество электронов наАтомное число1s2s3s4s4f5s5p2p3p4p3d4dИндий2 81818—2149Олово2 81818—2250Сурьма281818—2351Теллур281818—2452Йод281818—2553Ксенон281818—2654Ксенон также является благородным газом.
Оставшиеся подоболочки 4f (14 электронов), 5d (10), 5f (14) и 5g (18) перекрывают подоболочку 6s.
ЭлементКоличество электронов наАтомное число1s2s3s4s4f5s5d5f5g6s2p3p4p5p3d4dЦезий281818—8———155Барий281818—8———256У элементов начиная с лантана электроны появляются на подоболочках 4f и 5d, и эти элементы представляют собой уже несколько иную группу переходных элементов. Если у предыдущих групп переходных элементов (от скандия до цинка и от иттрия до кадмия) заполняемая электронная подоболочка перекрывалась лишь одним или двумя электронами следующей оболочки, то 4f подоболочка лантаноидов перекрывается не только двумя электронами 5s подоболочки, но и шестью электронами 5p и двумя электронами 6s. То есть у лантаноидов, в отличие от других переходных элементов, заполняется «более глубокая» подоболочка атома, которая сильнее перекрывается другими подоболочками. Именно поэтому лантаноиды настолько между собой похожи.
ЭлементКоличество электронов наАтомное число1s2s3s4s4f5s5d5f5g6s2р3p4p5p3d4dЛантан281818—81——257Церий281818181——258Празеодим28181838———259Неодим28181848———260Прометий28181858———261Самарий28181868———262Европий28181878———263Гадолиний28181878———264Тербий28181888———265Диспрозий28181898———266Гольмий281818108———267Эрбий281818118———268Тулий281818138———269Иттербий281818148———270Лютеций2818181481——271У лютеция и последующих элементов заполняется подоболочка 5d (до 10 электронов). Электроны этой подоболочки перекрываются двумя электронами подоболочки 6s, т. е. эти элементы являются обычными переходными элементами.
ЭлементКоличество электронов наАтомное число1s2s3s4s5s5d5f5g6s2p3p4p5p3d4d4fГафний28183282 — — 272Тантал28183283—— 273Вольфрам2 8183284—— 274Рений2 8183285—— 275Осмий2 8183286—— 276Иридий2 8183287—— 277Платина2 8183289—— 178Золото2 81832810——179Ртуть2 81832810— — 280У элементов начиная со ртути подоболочка 5d заполнена, подоболочки 5f и 5g остаются нетронутыми, а заполняется подоболочка 6p. Налицо такое же, как у элементов от бора до неона, соотношение электронов на s и p.
ЭлементКоличество электронов наАтомное число1s2s3s4s5s5f5g6s6p2p3p4p5p3d4d5d4fТаллий28183218——2181Свинец28183218——2282Висмут28183218——2383Полоний28183218——2484Астатин28183218——2585Радон28183218——2686Радон является благородным газом.
Остаются еще подоболочки 5f (14 электронов), 5g(18), 6d (10), 6f (14), 6g (18) и 6h (22). Все они перекрывают подоболочку 7s.
ЭлементКоличество электронов наАтомное число1s2s3s4s5s5f5g6s6d6f6g6h7s2p3p4p5p6p3d4d5d4fФранций28183218——8— ———187Радий28183218——8————288У следующих элементов электронные подоболочки заполняются так же, как и у лантаноидов.
ЭлементКоличество электронов наАтомное число1s2s3s4s5s5f5g6s6d6f7s2p3p4p5p6p6g3d4d5d6h4fАктиний28183218——81—289Торий28183218——82—290Протактиний281832182—8——291Уран281832183—8——292Нептуний281832184—8——293Плутоний281832185—8——294Америкум281832187—8——295Кюрий281832187—8——296Беркелий281832188—8——297Калифорний281832189—8——298Эйнштейний2818321810—8——299Фермий2818321811—8——2100Менделевий2818321812—8——2101Нобелий2818321813—8——2102Лавренций2818321814—8——2103Элементы от актиния до лавренция называются актиноидами. Хотя элемент с атомным числом 104 пока не открыт, у ученых есть все основания полагать, что его 104-й электрон займет подоболочку 6d, а химические свойства самого элемента будут схожи с гафнием.
Теперь становится очевидным, что в периодической таблице элементы расположены согласно размещению электронов на электронных оболочках их атомов.
Глава 6.
Дата: 2019-07-24, просмотров: 331.