При возникновении бета-излучения нейтрон внутри атомного ядра становится протоном. Ясно, что при этом изменяются и свойства атома.
Так как общее количество протонов возрастает на единицу, на единицу возрастает и атомное число, и такой атом становится уже атомом совсем другого химического элемента.
На самом деле радиоактивность некоего вещества практически всегда является признаком глубоких изменений свойств атомов этого вещества. Ученые осознали это через некоторое время после открытия радиоактивности и до того, как была изучена внутренняя структура ядра.
В 1900 году Крукс, один из первооткрывателей катодных лучей, обнаружил, что уран высокой очистки практически не проявляет радиоактивных свойств, и сделал вывод, что радиоактивность вызвана не самим ураном, а некой содержащейся в нем примесью.
В следующем году Беккерель подтвердил полученные Круксом результаты, а также выявил, что постепенно радиоактивность чистого урана возрастает до нормального для этого элемента уровня. В 1902 году Резерфорд совместно с английским физиком Фредериком Содди (1877–1956) обнаружил сходство поведения соединений тория с поведением урана.
Напрашивается логичный вывод: если радиоактивность вызвана примесью, то она постепенно образуется из самого урана. Другими словами, радиоактивность урана — показатель того, что атомы урана принимают какую-то другую форму. Эта новая форма атома также является радиоактивной и преобразуется в следующую и т. д. Исследования Резерфорда и Содди показали, что следует говорить не просто о радиоактивном элементе, а о ряде радиоактивных элементов.
Вполне возможно, что радиоактивность является свойством не урана и тория (сами элементы менее радиоактивны), а их разнообразных «дочерних элементов». Последние обладают гораздо большей радиоактивностью и либо присутствуют в составе урана и тория всегда, либо образуются в них сразу после очистки.
Раз «дочерние элементы» образуются медленно и быстро распадаются, значит, в руде урана и тория они содержатся лишь в исчезающе малых количествах. «Дочерние элементы» не поддаются обнаружению с помощью обычных химических методов, однако по испускаемым ими излучениям их можно обнаружить с большой точностью. Излучение каждого из дочерних элементов обладает своими уникальными характеристиками и интенсивностью.
В 1898 году Мария Кюри и ее муж, французский физик Пьер Кюри (1859–1906), обычными химическими методами разделили большое количество урановой руды по свойствам на фракции, отсеивая обладающие высокой радиоактивностью. В том же году им удалось обнаружить два неизвестных ранее элемента, первый из которых они назвали полоний (созвучно с названием родной страны Марии Кюри), а второй, из-за его высокой радиоактивности, — радий.
Радиоактивность этих элементов была гораздо выше, чем у урана и тория. На самом деле скорость распада радия и полония настолько высока, что ни один из них не дошел бы до наших дней в чистом виде, даже если 5 миллиардов лет назад, во время образования планеты, они существовали бы в достаточном количестве. Сегодня эти элементы существуют лишь благодаря тому, что они постоянно образуются из урана и тория. А вот скорость распада последних настолько низкая, что их запасы за 5 миллиардов лет практически не уменьшились, несмотря на постоянно продолжающийся процесс распада.
Сколько же существует таких «недолговечных» дочерних элементов урана и тория? Во времена Кюри никто точного ответа дать не мог, так как не было известно, сколько же еще осталось незаполненных клеток периодической таблицы. Концепция атомных чисел, разработанная Мозли в 1913 году, внесла в этот вопрос некоторую ясность.
Все элементы с атомными числами до 84 включительно (до висмута) являются нерадиоактивными, в том числе и еще неизвестные элементы (43, 91, 72 и 75). И действительно, гафний и рений, открытые в 1923-м и 1926 годах соответственно, оказались нерадиоактивными. Тогда ученые переключили свое внимание на элементы с атомным числом выше 83.
Торий (атомное число 90) и уран (атомное число 92) являются первыми открытыми радиоактивными элементами. Атомные числа обнаруженных Кюри полония (84) и радия (88) также выше 83.
Последовал целый ряд открытий. В 1899 году французский химик Андре Дебьерн (1874–1949) открыл актиний (атомное число 89); в 1900 немецкий химик Фридрих Дорн (1848–1916) открыл радон (атомное число 86); в 1917 году немецкий химик Отто Ган (1879–1968) совместно с австрийским физиком Лизе Майт-нер (1878–1968) открыл протактиний (атомное число 91).
Две оставшиеся ячейки этой части периодической таблицы, 85 и 87, оставались незаполненными еще целых 25 лет. Ученые были убеждены, что эти элементы также являются радиоактивными (что впоследствии и подтвердилось).
И тем не менее эти так замечательно вписывающиеся в таблицу элементы поставили перед химиками вопрос, который чуть было не опроверг сам принцип периодической системы, однако в итоге лишь в очередной раз доказал ее непоколебимость. Обо всем этом вы узнаете из следующей главы.
Глава 8.
ИЗОТОПЫ
Атомные превращения
Открытие в 1898 году нескольких новых элементов в радиоактивной руде вызвало некоторые затруднения. В периодической таблице было место лишь для 9 радиоактивных элементов (атомные числа от 84 до 92). То есть для радия, полония и некоторых других элементов место было, но что делать с остальными? Ведь если брать только дочерние элементы урана и тория с четко выраженными свойствами и определенной интенсивностью излучения, у физиков будет несколько десятков новых элементов.
Каждому типу излучения было дано свое название. Например, уран Xp, уран Xy, радий А, радий В и так далее вплоть до радия G. Были также излучения тория от А до D, два мезотория, один радиоторий и т. д. Но если элементов действительно столько же, сколько и различных излучений, как же их вписать в таблицу? С открытием Мозли атомного числа задача еще более усложнилась.
Для начала давайте рассмотрим природу этих радиоактивных излучений и их влияние на испускающий их атом. (Я прибегну к протонно-нейтронной модели атомного ядра, несмотря на то что изначально описываемый мною анализ был сделан на основе протонно-электронной модели.)
Возьмем произвольный элемент Q, ядро которого состоит из∙протонов и у нейтронов. Значит, его атомное число равняется x, а его атомный вес x + y. Запишем атомное число текстом нижнего регистра перед символом элемента, а атомный вес — текстом верхнего регистра после символа. Получаем xQx+y.
Теперь предположим, что атом этого элемента испустил одну альфа-частицу (обозначается греческой α). Альфа-частица состоит из двух протонов и двух нейтронов, следовательно, ее атомное число 2, а атомный вес 4. В записи это выглядит как 2α4.
То, что остается от исходного атома после выхода альфа-частицы, должно содержать x–2 протона и y–2 электрона. Атомное число уменьшается на 2 (и образуется новый элемент R), атомный вес — на 4. Это можно записать так:
xQx+y → x–2Rx+y–4 + 2α4 (Уравнение 8.1)
Если же исходный атом испустил бета-частицу (обозначается греческой β), ситуация будет несколько иной. Выход бета-частицы означает, что внутри ядра один нейтрон превратился в протон. Значит, теперь количество протонов в ядре будет x+1, а нейтронов у–1. Атомное число увеличится на 1, а атомный вес останется прежним, т. к. x + 1 + y – 1 = x + y.
Атомный вес самой бета-частицы практически равен 0. (Точнее, 0,00054, но в данном случае мы можем сократить его до 0.) Так как атомный вес равняется числу положительно заряженных частиц в ядре и так как бета-частица является электроном, а следовательно, обладает единичным отрицательным зарядом, ее атомное число равняется –1. Таким образом, бета-частицу можно обозначить как –1β0, а процесс выхода как
xQx+y → x+1Rx+y + –1β0 (Уравнение 8.2)
Обратите внимание, что в уравнениях 8.1 и 8.2 сумма атомных чисел правой части равняется сумме атомных чисел левой части в соответствии с законом сохранения электрического заряда. То же можно сказать и об атомных весах правой части формулы 8.2 согласно закону сохранения массы. (Пока мы можем пренебречь небольшим изменением массы при ее переходе в энергию.)
Гамма-луч обозначается греческой буквой γ. Гамма-излучение является электромагнитным, следовательно, не имеет ни атомного веса, ни атомного числа. Запись будет выглядеть как 0γ0. Добавляем следующую формулу:
xQx+y → xQx+y + 0γ0. (Уравнение 8.3)
Таким образом, когда атом испускает альфа-частицу, его атомное число уменьшается на 2, а атомный вес — на 4. Когда атом испускает бета-частицу, его атомное число уменьшается на 1, а атомный вес остается неизменным. Когда же атом испускает гамма-луч, его и атомное число, и атомный вес остаются неизменными. Этот закон впервые был сформулирован Содди в 1913 году.
Давайте применим этот закон к атому урана с атомным числом 92 и атомным весом 238, т. е. 92U238. Слабое радиоактивное излучение урана высокой очистки состоит из альфа-частиц. Испускание альфа-частицы уменьшает атомное число атома урана до 90, т. е. до атомного числа тория, а атомный вес до 234. Запись выглядит так:
92U238 → 90Th234 + 2α4. (Уравнение 8.4)
Атом тория, полученный в результате распада атома урана, несколько отличается от атома тория, содержащегося в руде. Атомное число последнего также равняется 90, однако его атомный вес равен 232, то есть 90Th232.
Атомное число и одного и другого атома равно 90, поэтому они оба занимают одну и ту же ячейку периодической таблицы. Содди обнаружил это в 1913 году и предложил называть элементы, имеющие одинаковое атомное число и различающиеся атомным весом, изотопами (от греч., означает «одно и то же место», то есть одно и то же место в периодической таблице).
Так как атомное число изотопов одного и того же элемента одинаково, химики решили на письме отображать лишь их атомные веса: торий–234 и торий–232, или, более кратко, Th232 и Th234.
С точки зрения химии вполне обоснованно помещать изотопы в одну и ту же ячейку периодической таблицы. Торий–234 и торий–232 имеют в ядре по 90 протонов и соответственно по 90 электронов в нейтральном атоме. Химические свойства элементов определяются распределением электронов по электронным уровням, а значит, химические свойства этих двух изотопов тория, как и изотопов любых других элементов, будут одинаковыми[131].
Но, несмотря на то что у атомов изотопов на энергетических уровнях один и тот же набор электронов, они все же отличаются структурой атомных ядер. Количество протонов в ядре изотопов одинаково, значит, неодинаково количество нейтронов. Например, ядро атома тория–234 состоит из 90 протонов и 144 нейтронов, в то время как ядро атома тория–232 состоит из 90 протонов и 142 нейтронов.
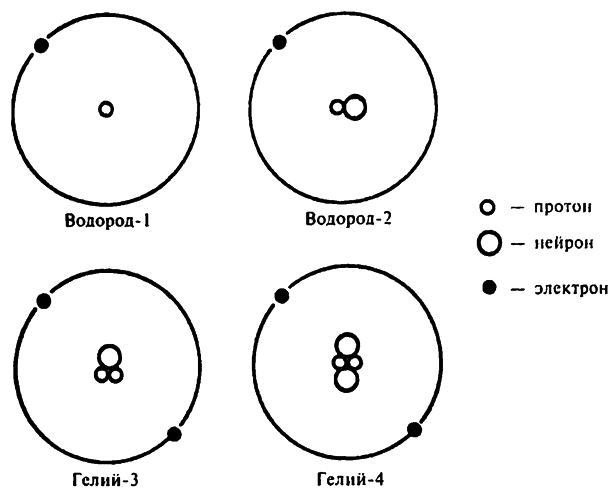
Простые изотопы
Когда речь идет об изменениях внутри атомного ядра, например когда мы говорим о радиоактивности (в то время как во время химических преобразований изменяется лишь число электронов, атомное ядро остается неизменным), различия в количестве нейтронов в ядре очень важны.
Итак, процесс распада тория–232 идет очень медленно, именно поэтому этот элемент до сих пор присутствует в земной коре. Атом тория испускает альфа-частицу и его атомное число падает до 88, т. е. до радия. Запишем это:
90Th234 → 91Pa234 + 2α4. (Уравнение 8.5)
С другой стороны, процесс распада атомов тория–234 идет крайне быстро, и именно поэтому в природе этот элемент встречается только в исчезающе малых количествах в урановой руде. Более того, при распаде тория–234 выделяется бета-частица, что приводит к увеличению атомного числа до 91, то есть до протактиния:
90Th234 → 91Ра234 + –1β0. (Уравнение 8.6)
После выхода альфа- или бета-частицы может образоваться новый атом, заряд ядра которого будет выше, чем у атома основного состояния. После возврата в прежнее состояние атом испускает гамма-луч. В некоторых случаях это происходит не сразу, атом существует какое-то время, а радиационное излучение его возбужденного ядра обладает уникальными характеристиками. Для обозначения наличия возбужденного ядра символ элемента помечают звездочкой. В процессе образования протактиния–234 его ядро переходит в возбужденное состояние:
91Pa234* → 91Pa234 + 0γ0. (Уравнение 8.7)
В 1936 году Лизе Майтнер предложила называть атомы с одинаковыми атомными числами и атомными весами, но различающиеся структурой ядра, изомерами. Первый случай ядерной изомерии был зафиксирован на примере протактиния–234 еще в 1921 году Отто Ганом, давним партнером Майтнер по работе.
Радиоактивные ряды
Закон Содди привел к отказу от собственных названий различных атомов, образующихся из урана и тория. Эти названия представляют определенный исторический интерес, поэтому их можно встретить в книгах по истории физики, но в этой книге мы будем обозначать эти элементы исключительно как изотопы. Как только мы правильно обозначим все эти элементы, окажется, что, несмотря на то что уран и торий образуют десятки изотопов, их все можно разместить в той или иной ячейке периодической таблицы.
В табл. 5 все вышесказанное проиллюстрировано на примере изотопов так называемого уранового ряда, то есть элементов, образующихся из урана–238.
Стоит подробнее ознакомиться с элементами этого ряда, как возникает несколько вопросов. Например, свинец–206 является стабильным изотопом и не подвергается радиоактивному распаду, поэтому этот элемент и заканчивает урановый ряд. Однако существуют и такие изотопы, как свинец–214 и свинец–210, и они являются радиоактивными элементами. Это говорит о том, что изотопы не обязательно являются радиоактивными, у одного и того же элемента могут быть как радиоактивные, так и устойчивые изотопы.
Если не принимать во внимание свинец–206, то процесс распада всех этих элементов, за исключением урана–238, идет с относительно высокой скоростью. Следовательно, с момента образования Земли до наших дней дошел только уран–238. Этот элемент является «родителем» всего уранового ряда, и если бы урана–238 сегодня не существовало, то не существовало бы и всех его дочерних элементов.
Таблица 5.
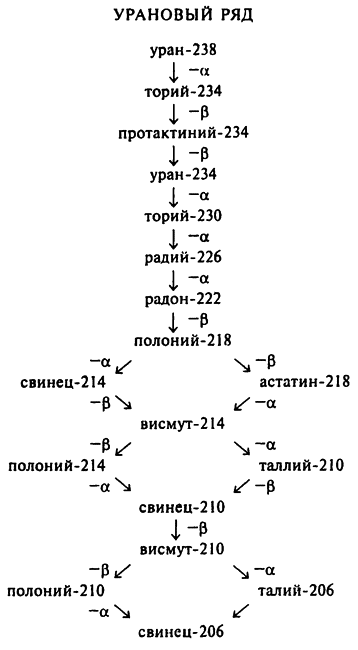
Атомы некоторых радиоактивных элементов могут образовывать разные цепочки изотопов. К примеру, полоний–218 может испускать альфа-частицы свинца–214 или же бета-частицу астатина–218. Это пример так называемого разветвленного распада. Как правило, преобладает какой-то один вариант распада. Например, лишь каждые 2 из 10 000 атомов полония–218 распадаются до астатина–218, все остальные распадаются до свинца–214. (То есть в этом случае преобладает эмиссия альфа-частиц, в других же случаях может преобладать и эмиссия бета-частиц.)
Астатин (атомное число 85) если и образуется во время радиоактивного распада, то обычно в самом конце цепочки превращений. Именно поэтому его количество настолько ничтожно мало, что ученые очень долго не могли его обнаружить. То же можно сказать и о франции (атомное число 87), с той лишь разницей, что франций в некоторых цепочках вообще не образуется.
Атомный вес любого атома радиоактивного семейства либо вообще не меняется (как в случае выхода бета-частицы или гамма-луча), либо уменьшается на 4 (как в случае выхода альфа-частицы). Это означает, что значение разницы атомных весов двух любых элементов ряда либо равно нулю, либо кратно 4.
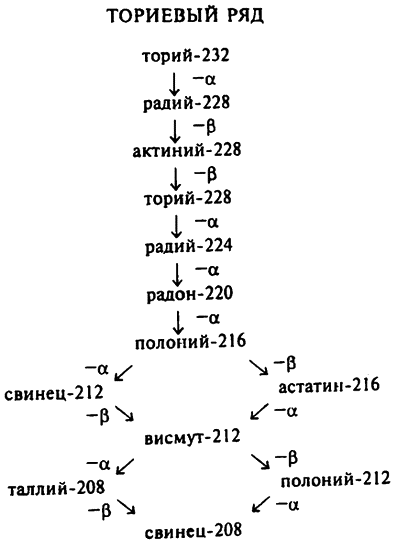
Таблица 6.
Атомный вес урана–238 равняется 238. Разделив 238 на 4, получаем 59 и 2 в остатке. При делении любого числа, отличного от 238 и кратного 4, на 4 всегда будет оставаться остаток 2. Значение атомного веса любого члена уранового ряда можно вычислить по формуле 4x + 2, где он может принимать любое значение от x = 59 — для урана–238 и x = 51 — для свинца–206. По этой причине урановый ряд иногда называют рядом 4x + 2.
После урана был открыт торий. Этот радиоактивный элемент также является родителем группы дочерних атомов так называемого ториевого ряда (см. табл. 6).
Атомные веса атомов изотопов тория, как и изотопов урана, также кратны 4. Значение атомного веса тория–232 равняется 232 и делится на 4 без остатка. Значения атомного веса всех элементов ториевого ряда также делятся на 4 без остатка, и поэтому изотопы тория иногда называют рядом 4x + 0.
Можно предположить, что раз из всех радиоактивных элементов в природе в значительных количествах встречаются только уран и торий, то существуют только два радиоактивных ряда. Однако в радиоактивных рудах встречают и атомы, значения атомных весов которых не удовлетворяют ни формуле 4х + 0, ни формуле 4x + 2, следовательно, эти атомы не принадлежат элементам ни уранового, ни ториевого ряда.
Сначала ученые решили, что эти элементы являются частью ряда актиния–227, значения атомного веса которого сводятся к формуле 4x + 3. Эти элементы получили название изотопов актиниевого ряда. В настоящее время это название все еще широко используется, несмотря на то что само предположение оказалось неверным. Процесс распада актиния–227 идет слишком быстро, поэтому этот элемент не мог просуществовать в течение 5 миллиардов лет, а значит, он не может быть и исходным атомом радиоактивного ряда.
Когда был открыт протактиний, ученые обнаружили, что при распаде протактиния–231 (по современной терминологии) образуется актиний–227, благодаря чему элемент и получил свое название («протактиний» означает «до актиния»). Однако процесс распада протактиния–231 также идет очень быстро, и этот элемент не может быть родителем ряда.
В 1935 году канадский физик Артур Джеффри Демпстер (1886–1950) обнаружил, что не все атомы урана являются атомами урана–238. Из каждой тысячи добываемых из урановой руды атомов урана семь являются атомами урана–235. Процесс распада этих атомов, ядро которых состоит из 92 протонов и 143 нейтронов, идет достаточно медленно (хотя и быстрее, чем распад урана–238), и атом урана–235 является родителем элементов актиниевого ряда. (Именно поэтому уран–235 иногда называют «актиноураном».) Значение атомных весов всех элементов актиниевого ряда (см. табл. 7) можно описать формулой 4x + 3.
Понятно, что должен существовать и четвертый ряд радиоактивных элементов, атомные веса которых могут принимать значение 4x + 1. Уран–233 как раз и является изотопом этого типа, и он не принадлежит ни к одному из вышеописанных рядов. Ученым так и не удалось обнаружить четвертый радиоактивный ряд ни в 1920-х, ни в 1930-х годах. Дело в том, что, как правильно предположили физики, ни один изотоп этого ряда не может являться исходным элементом, так как процесс распада всех элементов этого ряда идет слишком быстро.
В конце каждого из трех радиоактивных рядов стоит изотоп свинца с соответствующим атомным весом. Урановый ряд заканчивается свинцом–206 (4x + 2), ториевый ряд заканчивается свинцом–208 (4x + 0), а актиниевый ряд — свинцом–207 (4x + 3).
Таблица 7
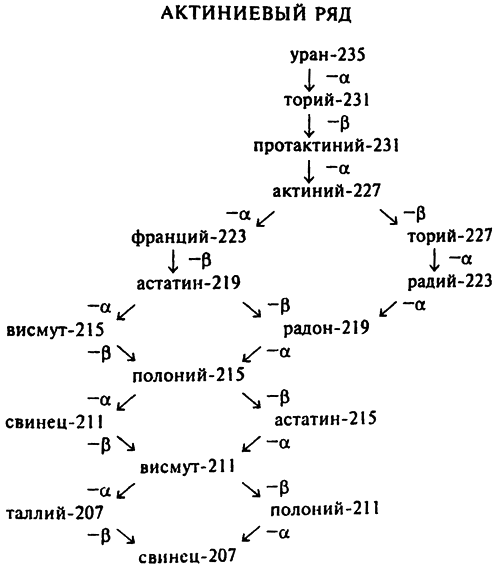
Все три изотопа свинца являются стабильными, а это означает, что у одного и того же элемента может быть не только по одному стабильному и нестабильному изотопу, но и более одного стабильного изотопа.
Период полураспада
Выше я давал процессу распада радиоактивных элементов характеристики типа «быстро» и «медленно», но не приводил никаких конкретных чисел.
Первыми продолжительность распада попытались вычислить Резерфорд и Содди в 1902 году. Они проследили изменение интенсивности излучения быстрораспадающегося радиоактивного изотопа и определили, что со временем интенсивность падает по экспоненте.
Это верно только в том случае, если за определенное количество времени распадается определенное количество атомов. Скажем, если скорость распада 0,02 всех атомов в секунду, то в первую секунду из 1 000 000 000 000 атомов радиоактивного вещества распадется 20 000 000 000 атомов. Конечно же мы не можем сказать, какие именно атомы распадутся. Мы не можем определить, распадется отдельно взятый атом в первую секунду, или через 5 секунд, или через 5 лет.
Приведу пример аналогичной ситуации из жизни. После тщательного изучения статистических данных страховые компании могут дать довольно точный прогноз, сколько человек из каждого миллиона американцев в возрасте 35 лет умрет в следующем году, если, конечно, считать этот год «нормальным». Компании не могут выявить конкретных американцев, которым грозит смерть, или предсказать конкретный год смерти конкретного американца. Они могут делать лишь общие прогнозы для большого количества абстрактных людей. Страховые компании работают с людьми, а физики — с атомами, и прогнозы последних, как правило, гораздо более точные.
Скорость радиоактивного распада не меняется с течением времени. Предположим, что каждый год умирает одно и то же количество человек. Предположим, что в течение года из 1 000 000 американцев в возрасте 35 лет умрет 0,2%, то есть 2000 человек. К концу года останется 998 000 человек. В следующем году умрет еще 0,2% от оставшихся, то есть 1996 человек. В следующем году умрет еще 0,2% от 996 004, останется 994 012 человек и т. д.
Таким образом, каждый год с уменьшением количества живущих будет уменьшаться и количество смертей. Невозможно предсказать конкретно, через сколько лет умрет последний человек, так как в любой произвольно взятый год умрет только небольшой процент людей. Понятно, что такой анализ дает приемлемые результаты только в том случае, если количество живых людей остается достаточно большим. Тем не менее если количество людей изначально было огромным, то согласно статистике некоторые из них проживут сотни и тысячи лет.
В действительности этого не происходит, потому что, когда человек стареет, постепенно возрастает вероятность его смерти, и вероятность смерти старых людей очень высока. Поэтому все 35-летние люди умрут менее через сто лет, независимо от их изначального количества.
В отличие от людей вероятность «смерти» атома радиоактивного элемента не возрастает со временем, и, если некоторые атомы распадаются мгновенно, отдельные атомы могут просуществовать в течение неопределенно больших периодов времени. Поэтому нельзя определить скорость полного распада радиоактивного атома, так как эта скорость может быть любой.
Однако при фиксированной скорости распада возникает одно интересное свойство: зная эту скорость, можно определить период времени, требующийся для распада половины исходного числа атомов. Этот период, который в 1904 году Резерфорд назвал периодом полураспада, одинаков для любого количества атомов в пределах разумного.
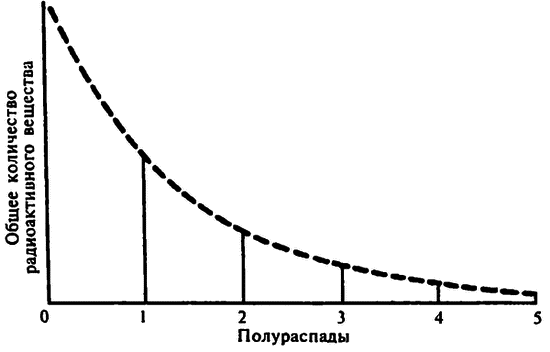
Полураспад
Оказалось, что период полураспада определенных изотопов не зависит от изменения условий внешней среды, таких как температура и давление. Физики научились немного (на несколько процентов) изменять период полураспада отдельных элементов, но это скорее исключение, чем правило.
Предположим, период полураспада некоего изотопа равен одному году. Тогда, если взять 2 триллиона атомов этого изотопа, к концу года от них останется только 1 триллион. Теперь атомов стало в два раза меньше, значит, в будущем году количество распадающихся атомов также уменьшится в два раза, то есть в следующем году распадется лишь полтриллиона атомов, а еще полтриллиона останется. К концу третьего года останется четверть триллиона и т. д.
В общем за первый период распадется половина любого количества атомов, за второй — половина оставшихся и так до бесконечности, пока количество атомов не станет слишком маленьким. В этом случае статистические методы просто перестанут давать точные результаты.
Зная период полураспада изотопа, можно определить, сколько его атомов распадется за определенное время, и таким образом оценить интенсивность его радиоактивного излучения. Также можно дать приблизительную оценку его интенсивности в прошлом и будущем.
Периоды полураспада радиоактивных изотопов могут быть как исчезающе короткими, так и чрезвычайно долгими. Период полураспада средней продолжительности можно определить непосредственно по скорости распада атомов элемента. Например, период полураспада радия–226 — 1620 лет.
Для определения продолжительности гораздо более длительных периодов используются косвенные методы. Возьмем, например, уран–238. Поскольку скорость распада его атомов очень мала, мы можем считать, что в течение определенного периода времени число атомов в куске урановой руды является константой. Обозначим это число Nu. За одну секунду распадается определенная часть F атомов урана. Таким образом, за одну секунду распадется FuNu атомов урана.
В процессе распада урана–238 образуется радий–226. Правда, это происходит не сразу: среди всех образующихся из урана–238 элементов радий–226 лишь пятый по счету. Но на данном этапе это для нас не имеет особого значения, поэтому давайте предположим, что из урана–238 сразу образуется радий–226.
Тогда так как за одну секунду распадается FuNu атомов урана, то за одну секунду образуется FuNu.
Радий–226 также начинает распадаться со скоростью FrNr атомов в секунду. Так как атомы радия–226 образуются из урана–238 и их число увеличивается, количество распадающихся атомов радия–226 также увеличивается до тех пор, пока не станет равным количеству образующихся атомов радия–226. Тогда количество атомов радии–226 становится постоянным, и это состояние называется радиоактивным равновесием урана–238 и радия–226. Математически это равновесие выражается так:
FuNu = FrNr (Уравнение 8.8)
или
Fu/Fr = Nr/Nu. (Уравнение 8.9)
То есть доля атомов определенного элемента, распадающихся за одну секунду, обратно пропорциональна периоду полураспада этого элемента. Чем длиннее период полураспада, тем меньше атомов в секунду распадается. Если принять за период полураспада урана–238 Hu радия–226 за Hr то
Fu/Fr = Hr/Hu. (Уравнение 8.10)
Теперь совместим уравнения 8.9 и 8.10:
Hr/Hu = Nr/Nu. (Уравнение 8.11)
Другими словами, при радиоактивном равновесии соотношение количества атомов элемента-родителя и дочернего элемента равно соотношению их периодов полураспада. В урановых рудах атомов урана–238, в 2 800 000 раз больше, чем атомов радия–226. Таким образом, период полураспада урана–238 должен быть в 2 800 000 раз дольше, чем у радия–226, то есть около 4 500 000 000 лет.
Теперь понятно, почему уран–238 все еще присутствует в земной коре. Если возраст Солнечной системы от 5 до 6 миллиардов лет, значит, от исходного количества атомов урана–238 распалось всего чуть более половины.
Период полураспада урана–235 короче, чем урана–238, — всего 713 000 000 лет. То есть со времени образования Солнечной системы до наших дней дошло около 1% атомов урана–235. Неудивительно, что из каждой тысячи атомов урана лишь 7 являются атомами урана–235.
Сегодня количество атомов любого радиоактивного изотопа с периодом полураспада менее 500 000 000 лет исчезающе мало, если только он не образуется из какого-то другого элемента с большим периодом полураспада. Из всех элементов ряда 4x + 2 приспособлен для жизни только уран–238, а из ряда 4x + 3 — только уран–235.
Из всех атомов ряда 4x + 0 продолжительностью полураспада, достаточной для того, чтобы являться родителем ряда, обладает лишь торий–232. Период его полураспада не менее 13 900 000 000.
Косвенным методом можно определить и гораздо более короткие периоды полураспада. Например, у изотопов, излучающих альфа-частицы, величина энергии этой частицы обратно пропорциональна периоду полураспада. Таким образом, зная энергию альфа-частиц (а ее можно определить по силе проникающей способности), можно высчитать продолжительность периода полураспада. Например, период полураспада полония–212 равен 0,0000003 секунды.
Если изотопы одного и того же элемента мало отличаются между собой по химическим свойствам, то они значительно отличаются по свойствам ядра, таким как период полураспада. Например, в то время как период полураспада тория–232 приблизительно 14 миллиардов лет, период полураспада тория–231 (у которого в ядре всего лишь на один нейтрон меньше) — всего лишь один день!
Стабильные изотопы
Обратив внимание на элементы трех радиоактивных рядов, представленных в табл. 5, 6, 7, можно заметить, что радиоактивные изотопы существуют и у устойчивых элементов. Например, у висмута таких изотопов пять — с атомным весом 210, 211, 212, 214 и 215, соответственно, у таллия — четыре — с атомным весом 206, 207, 208 и 210 и у свинца также четыре — с атомным весом 210, 211, 212 и 214. Так как все эти элементы содержатся в почве в больших количествах и не радиоактивны, у каждого из них должен быть хотя бы один стабильный изотоп.
Тем не менее все эти изотопы, как стабильные, так и нестабильные, являются радиоактивными. Напрашивается вопрос: а имеют ли изотопы нерадиоактивные элементы? Если имеют, то доказать это будет очень сложно, так как обычными лабораторными методами невозможно выделить изотопы (кроме некоторых исключительных случаев), да и радиоактивного излучения они не испускают.
Давайте предположим, что атомы элемента ионизированы, как в случае образования позитивных лучей (см. гл. 7). Тогда, так как в каждом атоме станет на один электрон меньше, их заряд будет равняться +1. Однако, если элемент состоит из двух и более изотопов, образуется несколько групп ионов, различающихся массой.
Если пропустить поток таких положительных ионов через магнитное поле, то они будут лететь по кривой траектории, причем степень крутизны будет зависеть от заряда и массы отдельных частиц. В данном случае заряд всех ионов одинаков, но масса-то различна! Чем легче частица, тем больше угол кривизны траектории ее полета. Теперь, если у всех ионов потока масса одинакова, то на фотопластинке они образуют одно пятно, однако если же поток электронов состоит из групп ионов с разными массами, то на пластинке будет уже несколько пятен, причем более тяжелые ионы образуют более темное и большее по размерам пятно.
В 1912 году Дж.Дж. Томсон, первооткрыватель электрона, проделал подобный эксперименте неоном. Положительные лучи из неона оставляли на фотопластинке два пятна, по всей видимости ионов неона–20 и неона–22. Первое пятно было почти в 10 раз больше второго. Это говорило о том, что неон состоит из двух изотопов, неона–20 и неона–22, в пропорции примерно 1/10. (Позднее было обнаружено присутствие и третьего изотопа, неона–21. Его содержание настолько мало, что из 1000 атомов неона 909 являются атомами неона–20, 88 — неона–22 и только 3 — атомами неона–21.)
В 1919 году работавший вместе с Томсоном английский физик Фрэнсис Уильям Астон (1877–1945) сконструировал более совершенное устройство для анализа положительных лучей. В этом устройстве положительные лучи определенной массы не просто оставляли отпечаток на фотопластинке; они особым образом отклонялись, и при этом повышалось разрешение. В результате пучок ионов одного элемента отпечатывался на фотопластинке в виде последовательности точек («массовый» спектр вместо оптического). По положению точек можно оценить массу отдельных изотопов, а по степени затемнения можно определить, с какой частотой эти изотопы встречаются в данном веществе (то есть относительное содержание). Устройство получило название масс-спектрограф.
С помощью масс-спектрографа ученые определили, что большинство устойчивых элементов состоят из двух и более стабильных изотопов. Полный список этих стабильных изотопов[132] приведен в табл. 8.
По данным таблицы можно сделать следующие выводы. Во-первых, несмотря на то что большинство из 81 устойчивого элемента имеют два и более стабильных изотопа (а у олова их целых 10), из них 20 элементов имеют всего один изотоп. (Более того, у двух элементов с атомным числом менее 84 вообще нет стабильных изотопов. Эти два элемента с атомными числами 43 и 61 подробно описаны в гл. 10.)
По правде говоря, элемент не может иметь «один изотоп», так как изотопы по определению являются двумя и более элементами, занимающими одну и ту же ячейку периодической системы. В данном случае элемент имеет «одного близнеца», и правильнее называть их нуклидами, то есть элементами с определенной структурой ядра. Тем не менее термин «изотоп» настолько прижился, что я буду продолжать говорить об «одном изотопе».
Не все из 282 приведенных в табл. 7 нуклидов действительно стабильны. 18 из них являются радиоактивными, однако их период полураспада настолько велик, что радиоактивное излучение у них очень слабое. Периоды полураспада некоторых из них достигают квадриллионов лет, поэтому их радиоактивностью можно просто пренебречь. Однако 7 из них очень радиоактивны, поэтому я и привел их в табл. 9.
Таблица 8.
СТАБИЛЬНЫЕ ИЗОТОПЫ
(Атомное число. Химический элемент … Изотопы)
1. Водород … 1, 2
2. Гелий … 3, 4
3. Литий … 6, 7
4. Бериллий … 9
5. Бор … 10, 11
6. Углерод … 12, 13
7. Азот … 14, 15
8. Кислород … 16, 17, 18
9. Фтор … 19
10. Неон … 20, 21, 22
11. Натрий … 23
12. Магний … 24, 25, 26
13. Алюминий … 27
14. Кремний … 28, 29, 30
15. Фосфор … 31
16. Сера … 32, 33, 34, 36
17. Хлор … 35, 37
18. Аргон … 36, 38, 40
19. Калий … 39, 40, 41
20. Кальций … 40, 42, 43, 44, 46, 48
21. Скандий … 45
22. Титан … 46, 47, 48, 49, 50
23. Ванадий … 50, 51
24. Хром … 50, 52, 53, 54
25. Марганец … 55
26. Железо … 54, 56, 57, 58
27. Кобальт … 59
28. Никель … 58, 60, 61, 62, 64
29. Медь … 63, 65
30. Цинк … 64, 66, 67, 68, 70
31. Галлий … 69, 71
32. Германий … 70, 72, 73, 74, 76
33. Мышьяк … 75
34. Селен … 74, 76, 77, 78, 80, 82
35. Бром … 79, 81
36. Криптон … 78, 80, 82, 83, 84, 86
37. Рубидий … 85, 87
38. Стронций … 84, 86, 87, 88
39. Иттрий … 89
40. Цирконий … 90, 91, 92, 94, 96
41. Ниобий … 93
42. Молибден … 92, 94, 95, 96, 97, 98
44. Рутений … 86, 98, 99, 100, 101, 102, 104
45. Родий … 103
46. Палладий … 102 104, 105, 106, 108, 110
47. Серебро … 107 109
48. Кадмий … 106 108, 110, 111, 112, 113, 114, 116
49. Индий … 113 115
50. Олово … 112 114, 115, 116, 117, 118, 119, 120, 122, 124
51. Сурьма … 121 123
52. Теллур … 120 122, 123, 124, 125, 126, 128, 130
53. Йод … 127
54. Ксенон … 124 126, 128, 129, 130, 131, 132, 134, 136
55. Цезий … 133
56. Барий … 130 132, 134, 135, 136, 137, 138
57. Лантан … 138 139
58. Церий … 136 138, 140, 142
59. Празеодим … 141
60. Неодим … 142 143, 144, 145, 146, 148, 150
62. Самарий … 144 147, 148, 149, 150, 152, 154
63. Европий … 151 153
64. Гадолиний … 152 154, 155, 156, 157, 158, 160
65. Тербий … 159
66. Диспрозий … 156, 158, 160, 161. 162, 163, 164
67. Гольмий … 165
68. Эрбий … 162, 164, 166, 167, 168, 170
69. Тулий … 169
70. Иттербий … 168, 170, 171, 172, 173, 174, 176
71. Лютеций … 175, 176
72. Гафний … 174, 176, 177, 178, 179, 180
73. Тантал … 180, 181
74. Вольфрам … 180, 182, 183, 184, 186
75. Рений … 185, 187
76. Осмий … 184, 186, 187, 188, 189, 190, 192
77. Иридий … 191, 193
78. Платина … 190, 192, 194, 195, 196, 198
79. Золото … 197
80. Ртуть … 196, 198, 199, 200, 201, 202, 204
81. Таллий … 203, 205
82. Свинец … 204, 206, 207, 208
83. Висмут … 209
Может показаться странным, что радиоактивность не была обнаружена ранее, особенно на примере калия–40, так как калий — вполне обычный химический элемент, а у калия–40 (входит в список элементов табл. 9) период полураспада короче, чем у урана–238 и урана–232, поэтому он и более радиоактивный.
На то есть две причины. Во-первых, в природе калий–40 встречается довольно редко: из 10 000 атомов калия только 1 является атомом калия–40. Во-вторых, хотя и уран, и торий являются родителями ряда очень радиоактивных элементов, именно их дочерние элементы порождают явления, которые наблюдали Беккерель и Кюри.
Ни один из радиоактивных элементов с длинным периодом полураспада, являющийся изотопом более легких элементов, не может быть родителем радиоактивного ряда. Они испускают бета-частицу и тут же становятся стабильными изотопами элемента с атомным числом, больше на 1. Таким образом, рубидий–87 становится устойчивым стронцием–87, лантан–138 становится устойчивым церием–138 и т. д.
У калия–40 все немного по-другому. Около 89% всех распадающихся атомов калия–40 действительно излучают бета-частицу и превращаются в устойчивый кальций–40. Ядра оставшихся 11% атомов поглощают электрон К-оболочки (см. гл. 5), и этот процесс получил название К-захват. Этот захваченный электрон нейтрализует положительный заряд протона, и в итоге в ядре появляется еще один нейтрон. При этом количество нуклонов не меняется, а следовательно, и атомный вес остается прежним, но вот атомное число уменьшается на 1. Путем К-захвата калий–40 (атомное число 19) становится устойчивым аргоном–40 (атомное число 18).
В какой-то мере самым необычным из всех стабильных изотопов является водород–2, ядро которого состоит из одного протона и одного нейтрона, в отличие от ядра водорода–1, которое состоит только из одного протона. Соотношение разницы массы у этих двух элементов намного больше, чем у двух любых стабильных изотопов любого другого элемента.
Например, масса урана–238 в 238/235, или 1,013, раза больше массы урана–235, олова–124 (самый тяжелый изотоп этого элемента) — в 1,107 раза больше массы олова–112 (самого легкого). Масса кислорода–18 в 1,125 раза больше массы кислорода–16. А масса водорода–2 в 2 раза больше массы водорода–1.
Эта огромная разница относительной массы двух изотопов водорода говорит о том, что по физическим и химическим свойствам эти два элемента отличаются друг от друга сильнее, чем изотопы других веществ. Точка кипения обычного водорода 20,38 °К, а у водорода–2 («тяжелый водород») — 23,50 °К.
Опять-таки плотность обычной воды — 1000 граммов на кубический сантиметр, а температура замерзания 273,1 °K (0 °С), в то время как у воды, молекулы которой состоят из водорода–2 («тяжелой воды»), плотность 1,108 грамма на кубический сантиметр, а температура замерзания — 276,9 °К (3,8 °С).
Учитывая все особенности водорода–2, ему дали особое название — дейтерий (от греч. «второй»). Его символ — D, и формула тяжелого водорода выглядит как D2, а тяжелой воды — D2O.
Физики предположили возможность существования дейтерия еще в самые первые годы изучения изотопов, так как атомный вес водорода был немного выше, чем он должен быть.
Таблица 9.
Дата: 2019-07-24, просмотров: 373.