Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

В XIX веке химики все больше убеждались, что масса не может ни появляться ниоткуда, ни исчезать в никуда (закон сохранения массы).  Однако Лоренцу и Эйнштейну казалось, что масса появляется при увеличении скорости и исчезает при уменьшении скорости. Конечно, изменения массы на обычных скоростях крайне малы, но они есть. Откуда же тогда берется масса и куда исчезает?

Начнем с того, что представим, что к телу определенной массы (m)  прикладывается определенная сила (f). В таких условиях тело получает ускорение (a),  а из второго закона Ньютона (см. ч. I) можно сделать вывод, что a =f/m.  Присутствие ускорения означает, что скорость тела увеличивается, но в старой ньютоновской модели Вселенной это не влияло на массу тела, она оставалась постоянной. Если силу также рассматривать как постоянную, то f/m  тоже остается постоянным и a , ускорение, тоже постоянно. В результате такого постоянного ускорения скорость тела (в ньютоновском представлении) будет возрастать неограниченно и достигнет любого значения, которое вы назовете, — надо только дождаться.

В эйнштейновской же Вселенной наблюдатель, измеряющий скорость объекта, к которому прикладывается непрерывная постоянная сила, никогда не сможет увидеть, как скорость этого объекта превысит скорость света в вакууме. Следовательно, хотя его скорость и возрастает под воздействием постоянной силы, эта скорость возрастает все меньше и меньше и по мере приближения к скорости света она увеличивается гораздо меньше. Короче, ускорение тела под влиянием постоянной силы уменьшается по мере увеличения скорости и становится нулевым, когда скорость достигает световой.

Но опять же по второму закону Ньютона масса тела равна силе, к нему прилагаемой, поделенной на ускорение, производимое этой силой, то есть m = f/a.  Если сила постоянна, а ускорение уменьшается по мере увеличения скорости, то a  уменьшается по мере увеличения скорости, а f — нет; следовательно, f/a  увеличивается по мере увеличения скорости. А это означает, поскольку m = f/a,  что масса увеличивается вместе со скоростью. (Так увеличение массы по мере увеличения скорости можно вывести из эйнштейновского допущения о постоянстве скорости света в вакууме.)

Подвергаясь воздействию силы, тело получает кинетическую энергию, которая равна половине его массы, умноженной на квадрат его скорости (ek =  ½mv2, см. ч. I). С ньютоновской точки зрения это увеличение кинетической энергии вытекает только из увеличения скорости, поскольку масса считается неизменной. С эйнштейновской же точки зрения это увеличение кинетической энергии является результатом увеличения как скорости, так и массы.

В случаях, когда масса не задействована в изменениях энергии (как гласит точка зрения Ньютона), естественно представлять себе массу как что-то не имеющее отношения к энергии и думать, что, с одной стороны, существует закон сохранения энергии, а с другой — закон сохранения массы и оба закона самостоятельны.

Если же масса меняется и, таким образом, является тесно задействованной в процессах изменения энергии (как это представлял Эйнштейн), естественно думать о массе и энергии как о различных аспектах одного и того же, поэтому закон сохранения энергии будет включать в себя и массу. (Чтобы это стало абсолютно понятным в свете наших предыдущих выводов, мы иногда говорим о законе сохранения массы-энергии, но слово «масса» не является действительно обязательным.)

Движение не создает массу в любом реальном ощущении; масса — лишь один из аспектов общего возрастания кинетической энергии, получаемой из силы, на которую расходуется энергия где-то в другой части системы.

Но предположим теперь, что закон сохранения энергии (включающий в себя массу) остается действительным в релятивистской вселенной (а похоже, так оно и есть). По этому закону, хотя энергия и не может ни появляться, ни исчезать, она может переходить из одной формы в другую. Это означает, что определенное количество массы может быть конвертировано в определенное количество других форм энергии, таких как тепло, например, и что определенное количество энергии в другой форме, например тепло, может, следовательно, конвертироваться в определенное количество массы. А это и есть то, на чем настаивал Эйнштейн.

Равнозначность массы и энергии, объявленная Эйнштейном в его работе 1905 года, стала активно использоваться физиками его времени. Открытие тремя годами позже радиоактивности (частично я буду говорить об этом в III части), казалось, показало ситуацию, в которой энергия бесконечно порождалась из ниоткуда. Когда специальная теория относительности указала путь, ученые стали искать исчезновение массы — и нашли его.

Может показаться удивительным, что никто не заметил взаимных изменений массы и энергии, пока Эйнштейн не вывел их теоретически. Причина этого кроется в самой природе эквивалентности — в точном определении того, какое количество энергии соответствует какому количеству массы.

Чтобы определить это, давайте возьмем обращенный коэффициент Фитцджеральда, равный 1/√(1 – v 2/c2).  Это также можно записать, следуя алгебраическим преобразованиям, как (1 – v2c2)–½. Выражение, записанное этим образом, можно сказать, принадлежит типу (1 – b)–a.  По теореме о биноме (математическое отношение, впервые разработанное самим Ньютоном) выражение (1 – b) –a может быть развернуто в бесконечную последовательность слагаемых, начинающуюся так: 1 + ab + ½(a2 + 1)b2 + …

Чтобы применить это к обращенному коэффициенту Фитцджеральда, примем a  = ½, a b = v2/c2.  Тогда коэффициент Фитцджеральда становится равным:

 

1 + v2/2c2 + 3v4/8c4 + …

 

Поскольку c, скорость света, принято считать имеющей постоянную величину, то второе и третье слагаемые (как и все последующие слагаемые этой бесконечной последовательности) увеличиваются по мере возрастания v. Но v достигает максимума тогда, когда скорость движущегося тела достигает скорости света (по крайней мере, большей скорости мы измерить не можем). Следовательно, различные слагаемые тогда достигают наибольшей величины, и при v = с последовательность принимает вид 1 + ½ + 3/8 …

Уменьшение становится еще более резким на более низких скоростях, и последующие слагаемые становятся все более и более незначительными. Когда v = c/2 (150 000 километров в секунду), эта последовательность выглядит как 1 + 1/8 + 3/128… Когда v = c/4 (75 000 километров в секунду), серия выглядит как 1 + 1/32 + 1/2048…

Такого рода уменьшающийся ряд показывает, что завершающая часть последовательности (несмотря на то, что она бесконечна) приходит к конечному небольшому объему. Следовательно, мы можем устранить все члены последовательности, кроме нескольких первых, и рассматривать эти несколько первых как всю последовательность в достаточно точном приближении.

К примеру, на обычных скоростях все слагаемые последовательности, кроме первого (который всегда равняется 1), принимают такие крошечные значения, что их можно полностью игнорировать. В таком случае обращенный коэффициент Фитцджеральда можно рассматривать как равный единице с большой степенью приближения (именно поэтому изменения в массе и длине оставались до XX столетия незамеченными). Чтобы сделать его еще более точным, особенно на очень высоких скоростях, мы можем рассматривать два первых слагаемых серии. Это достаточно точно для всех реальных целей, и о третьем и дальнейших слагаемых можно уже не думать.

Тогда с достаточной точностью можно сказать, что

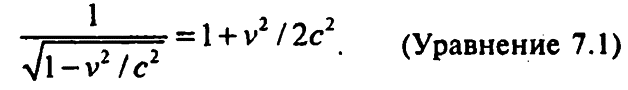
Теперь же давайте вернемся к отношению массы Лоренца (уравнение 6.7), которое утверждает, что масса тела в движении (m1) равна его массе покоя (m0), поделенной на коэффициент Фитцджеральда. Это то же самое, что сказать, что m1 равно m0, умноженному на обращенный коэффициент Фитцджеральда; следовательно, используя новое выражение для этого обращения, данного в уравнении 7.1, мы можем написать отношение массы в следующем виде:

 

m1 = m0(l + v2/2c2) = m0 + m0v2/2с2.  (Уравнение 7.2)

 

Увеличение массы в результате движения, то есть m1 – m0, мы назовем просто m.  Решив уравнение 7.2 для m1– m0,  то есть для m, мы найдем, что

 

m = m0v2/2c2 = ½m0v2/c2. (Уравнение 7.3)

 

Выражение ½m0v2 из правой части уравнения 7.3 оказывается значением кинетической энергии движущегося тела (кинетическая энергия равна ½mv2, см. ч. I), которое обладает своей массой покоя. На самом же деле оно обладает чуть большей массой благодаря факту своего движения, но за исключением случаев особо высоких скоростей реальная масса его лишь немногим больше массы покоя — столь немногим, что на практике мы можем считать ½m0v2 равным его кинетической энергии и быть уверенными в том, что это достаточно точно. Если мы обозначим эту кинетическую энергию как e,  то уравнение 7.3 примет вид:

 

m = е/с2.  (Уравнение 7.4)

 

Вспомним о том, что т  представляет прибавление массы, получаемое в ходе движения. Поскольку очень быстрое движение, представляющее очень большое значение e  (кинетической энергии), производит лишь небольшой прирост массы, мы ясно видим, что большая часть обыденной энергии равна крошечному количеству массы. Для подсчета отношения можно использовать уравнение 7.4, простым преобразованием приводимое к привычному виду:

 

e = тс2.  (Уравнение 7.5)

 

В системе СГС (см. ч. I), где все единицы измерения воспроизводятся из сантиметров, граммов и секунд, значение c  (скорости света в вакууме) — 30 000 000 000 сантиметров в секунду. Соответственно значение c2 = 900 000 000 000 000 000 000 см2/с2. Если принять за m  один грамм, то mc2 равняется 900 000 000 000 000 000 000 граммов на сантиметр в квадрате в секунду в квадрате, или, поскольку 1 г на см2/с2 определяется как «эрг», 1 грамм массы равен 900 000 000 000 000 000 000 эргов энергии.

Одна килокалория равна 41 860 000 000 эргов. Это означает, что 1 грамм массы равен 21 500 000 000 килокалорий. Сгорание галлона бензина освобождает около 32 000 килокалорий. Этому количеству энергии соответствует масса в 32000/21500000000, то есть 1/670000 грамма. Это означает, что сгорание целого галлона бензина, перевод энергии в тепло, свет, механическое движение поршней и т. д. приносит системе в целом потерю массы в 1/670000 грамма. Неудивительно, что химики и физики не замечали столь малых изменений, пока не стали искать их специально.

С другой стороны, если бы целые граммы массы можно было полностью перевести в энергию, эта обширная концентрация произведенной энергии имела бы огромное действие. В части III будут перечислены шаги, по которым постепенно стало понятным, как это сделать. В результате этого появились атомные бомбы,  угрожающие уничтожить все человечество, и атомные реакторы,  дающие человечеству новую надежду на будущее.

Еще уравнение 7.5 предлагает первое удовлетворительное объяснение того, откуда берут энергию Солнце и другие звезды. Для того чтобы излучать столько энергии, сколько оно излучает, Солнце должно терять 4 600 000 тонн массы ежесекундно. Это довольно много по человеческим меркам, но незначительно для Солнца. Такими темпами оно может излучать практически неизменно еще миллиарды лет.

Формула Эйнштейна, e = mc2,  как вы видите, полностью происходит из допущения о постоянстве измеряемой скорости света, и само наличие атомных бомб является страшным свидетельством верности специальной теории относительности. Неудивительно, что из всех физических формул e = mc2 получила наибольшую известность среди населения, не имеющего отношения к физике.

 

 

Относительность времени

 

Эйнштейн пошел еще дальше в своих выводах из своих же допущений и вышел за рамки рассуждений Лоренца — Фитцджеральда о длине и массе, подойдя к обсуждению времени.

Время всегда измеряется посредством некоего ровного периодического движения: вращения Земли, капанья воды, ударов метронома, колебаний маятника, лаже вибраций атома в молекуле. Однако перемены в длине и массе при возрастании скорости неизбежно должны привести к замедлению любого периодического движения. Следовательно, время должно измеряться, как протекающее все медленнее по мере возрастания скорости относительно наблюдателя.

И вновь нам потребуется коэффициент Фитцджеральда. Так, промежуток времени (t), наблюдаемый на теле, движущемся с данной скоростью относительно промежутка времени в покое (t0), вычисляется так:

 

t = t0√(1– v2 /с2 ) (Уравнение 7.6)

 

На скорости в 260 000 километров в секунду относительно наблюдателя t будет равным t0/2.  Другими словами, потребуется час времени наблюдателя на то, чтобы пронаблюдать, как на движущемся объекте проходит полчаса. То есть если на часах наблюдателя было 1.00 и на часах на движущемся объекте было 1.00, то через час на часах наблюдателя будет 2.00, а на часах на движущемся объекте будет только 1.30.

На скорости, равной скорости света, t  будет равно 0. Следовательно, для того чтобы соответствовать любому промежутку часов наблюдателя, часам движущегося объекта потребуется вечность. Насколько наблюдатель сможет заметить, часы на движущемся объекте всегда будут показывать 1.00; время на объекте застынет. Это замедление времени в зависимости от движения называется растяжением времени.

Такое положение дел кажется странным, но это было проверено на определенных короткоживущих субатомных частицах. Двигаясь медленно, они распадались за определенное фиксированное время. Двигаясь же очень быстро, они продолжали существовать значительно дольше, прежде чем распадались. Естественно сделать вывод, что мы наблюдали замедление времени для быстро движущихся частиц. Они все еще распадаются через, скажем, одну миллионную секунды, но для нас эта миллионная секунды растягивается из-за того, что частица быстро движется.

Как и в случае с длиной и массой, это изменение времени является только изменением измеряемой величины (пока мы остаемся верными принципам специальной теории) и изменяется вместе с наблюдателем.

Вернемся к примеру, к пролетающим друг мимо друга космическим кораблям Х  и Y.  Люди на корабле Х,  видя, как мимо них пролетает корабль Y со скоростью 260 000 километров в секунду, и наблюдая маятниковые часы на борту корабля Y,  будут видеть, что эти часы отбивают секунду за две секунды времени. Все на корабле Y  будет занимать в два раза больше времени (или так будет казаться наблюдателю на корабле X).  Даже атомы будут двигаться со скоростью в два раза меньше положенной.

Люди на корабле Y  конечно же не знают об этом. Считая себя находящимися в покое, они будут настаивать на том, что это на корабле X  время замедленно. (На самом деле, если бы корабли пролетали друг мимо друга таким образом, чтобы каждому скорость другого казалась равной скорости света, каждый настаивал бы на том, что на другом корабле время полностью остановилось.)

Однако вопрос о времени хитрее, чем вопрос о длине и массе. Если космические корабли после такой мимолетной встречи сопоставить вместе в состоянии покоя, их длина и масса снова станут «нормальными» и никаких следов их изменений не останется, поэтому вопрос «реальности» отпадает.

Но что касается времени… Находясь во взаимном покое, часы снова идут на обоих кораблях в одинаковом темпе. Однако следы от предыдущих расхождений во времени остаются. Если одни часы были замедленны и в прошлом проходили только полчаса, пока другие проходили час, то теперь первые часы будут на полчаса отставать! Каждый корабль будет твердо настаивать, что на другом часы отмеряли время медленнее, и каждый будет ожидать, что часы другого отстали.

Будет ли так? Будут ли чьи-либо часы отставать? А если да, то чьи?

Это парадокс часов,  который хорошо известен физикам.

Если четко придерживаться условий специальной теории, то есть если оба корабля вечно продолжают равномерное движение, парадокса часов не будет. В этом случае они никогда больше не встретятся, и различие в измерениях останется непроверяемым на предмет «реальности».

Для того чтобы корабли сошлись вместе, как минимум, один из них должен замедлиться, выполнить поворот, набрать скорость и догнать другой.

Все это — неравномерное движение, или ускорение, что тут же выводит нас за рамки специальной теории.

Эйнштейн работал над подобными проблемами десять лет после провозглашения своей специальной теории и в 1915 году опубликовал общую теорию относительности , в которой рассматриваются последствия неравномерного, или ускоренного, движения. Это более тонкий и сложный аспект относительности, чем специальная теория, и не все физики-теоретики полностью согласны с выводами обшей теории.

Предположим, что наши космические корабли — одни во Вселенной. Корабль Y  замедляет движение, разворачивается и ускоряется так, чтобы стать бок о бок с кораблем X.  Но по принципам относительности люди на корабле Y имеют полное право считать себя находящимися в покое. А если они рассматривают себя как находящихся в покое, то, с их точки зрения, это корабль X  замедляет движение, разворачивается и ускоряется так, чтобы вернуться к ним. То, что люди с корабля X  наблюдают по отношению к кораблю Y, то люди на корабле Y  наблюдают по отношению к кораблю X. Поэтому вполне возможно, что, когда корабли в конце концов окажутся бок о бок, часы на них каким-то образом покажут одно и то же время.

Однако на самом деле этого не произойдет, потому что эти корабли во Вселенной не одни. Вселенная наполнена большим количеством материи, и присутствие этого количества материи разрушает симметрию ситуации кораблей X  и Y.

Так, если корабль Y выполняет разворот, корабль X наблюдает, как он это делает. Но, считая себя находящимся в покое, корабль X  продолжает видеть, как вся остальная Вселенная (звезды и галактики) пролетают мимо него с постоянной равномерной скоростью, отражающей его собственную постоянную равномерную скорость. Другими словами, корабль X видит, что корабль Y, и только он,  проделывает неравномерное движение.

С другой стороны, если корабль Y считает себя находящимся в покое, он наблюдает, что не только корабль X подвергается ускорению, но и вся остальная Вселенная вместе с ним.

Другими словами, оба корабля подвергаются неравномерному движению относительно друг друга, но Вселенная в целом подвергается неравномерному движению только относительно корабля Y.  Два корабля, вполне естественно, подвергаются разному воздействию вследствие огромной разницы в их истории, и когда их сводят вместе, то именно на корабле Y  (который подвергался неравномерному движению по отношению ко всей Вселенной) часы будут отставать. Парадокса нет, поскольку получится, что команды обоих кораблей наблюдали неравномерное движение Вселенной по отношению к кораблю Y и оба согласны по поводу разницы в истории кораблей и не могут спрятаться за утверждение «моя система отсчета не хуже, чем твоя».

Теперь предположим, что космический путешественник покидает Землю и по прошествии некоторого времени удаляется от нас со скоростью, близкой к световой. Если бы мы могли наблюдать, как он путешествовал, мы бы видели, как его время проходит раз в сто медленнее, чем наше. Если бы он наблюдал нас, он бы видел, как наше время проходит в сто раз медленнее, чем его. Другими словами, если бы, поворачивая, он настаивал на том, что находится в покое, ему пришлось бы тогда признать, что вся Вселенная поворачивается вокруг него. Эффектом этого будет уменьшение промежутка времени для него, если речь идет и о нем, и о оставшихся дома землянах.

Путь туда-обратно может показаться ему длившимся всего год, но на Земле может пройти сто лет. Если бы у нашего космонавта был брат-близнец, оставшийся на Земле, этот брат давно мог умереть от старости, в то время как наш космонавт едва ли постарел бы. (Это называется парадоксом близнецов.)  Однако важно понимать, что космический путешественник не обнаружил источника вечной молодости. Он мог состариться только на год за земной век, но он и прожил за этот земной век всего год. Более того, независимо от его скорости время ни для него, ни для его наблюдателей, находящихся на Земле, не повернет вспять. Моложе он никогда не станет.

Изменяемость времени в зависимости от изменений скорости разрушает наши представления об абсолютности времени. Из-за этого становится невозможным определить время события таким образом, чтобы все наблюдатели согласились с этим. Вдобавок к этому время ни одного события не может быть определено, пока информация об этом событии не дойдет до наблюдателя, а эта информация может распространяться только со скоростью света.

В качестве простого примера давайте представим, что космический путешественник возвращается на Землю, для него прошел один год, и он обнаруживает, что его брат-близнец умер пятьдесят лет назад по земному времени. Для путешественника это может показаться невозможным, ведь по его меркам пятьдесят лет назад его брат еще не родился.

На самом деле в математическом обосновании теории относительности нет смысла работать отдельно с пространством или отдельно со временем. Вместо этого уравнения описывают их объединение (обычно именуемое пространство-время). Чтобы разместить точку на прстранстве-времени, надо назвать координаты на каждом из трех пространственных измерений и значение времени; время при этом рассматривается как подобное (хоть и не в точности) трем обычным измерениям. Именно в этом смысле время называют «четвертым измерением».

Иногда утверждают, что существование относительного времени позволяет измерять скорости больше световой. Допустим, к примеру, что космический корабль летит от Земли до некоей планеты, находящейся на расстоянии десяти световых лет, и делает это так быстро, что вследствие растяжения времени команде кажется, что путешествие заняло всего год.

Поскольку корабль, путешествуя всего год, прошел расстояние, на преодоление которого свету требуется десять лет, не означает ли это, что он двигался со скоростью в десять раз больше световой?

Правильный ответ — не означает. Если бы члены команды начали отстаивать это мнение, они бы измеряли промежуток времени в один год в своей собственной системе отсчета, а расстояние от планеты до Земли (десять световых лет) — в системе отсчета Земли. Вместо этого им следовало бы спросить: каково расстояние от Земли до планеты в системе отсчета корабля?

В системе отсчета корабля корабль, разумеется, неподвижен, а Вселенная в то же время, включая Землю и планету-цель, проскакивает назад на огромной скорости. Вся Вселенная сокращена, как и следует ожидать из сокращения Фитцджеральда (см. гл. 6), и расстояние от Земли до конечной планеты гораздо меньше чем десять световых лет. На самом деле оно меньше одного светового года, так что корабль может преодолеть это расстояние за один год, не превышая скорости света.

Опять же, хотя кораблю потребовался всего год, чтобы добраться до цели, это не значит, что он обогнал свет, даже несмотря на то, что лучу света, вылетевшему с Земли одновременно с кораблем, потребуется десять лет на то, чтобы преодолеть расстояние в десять световых лет. Этот промежуток — десять световых лет — будет истинным только в рамках земной системы отсчета. В собственной же системе отсчета луча, поскольку он движется со скоростью света, затраченное время сократится до нуля, и луч света попадет на альфу Центавра (или любое другое место во Вселенной, сколь угодно удаленное), не тратя на это времени вообще.

Это нельзя использовать как аргумент в пользу того, что в системе отсчета светового луча его скорость в таком случае бесконечна, поскольку в собственной системе отсчета светового луча вся толща Вселенной сокращается до нуля в направлении его движения. Пересечение Вселенной нулевой толщины не займет у света времени, даже если скорость конечна и составляет всего 300 000 километров в секунду.

 

 

Общая теория

 

Одним из базовых допущений специальной теории является невозможность измерить абсолютное движение; допущение о том, что ни один наблюдатель не может присвоить себе привилегию считать себя находящимся в покое и что все системы отсчета равно действительны.

Если же рассмотреть неравномерное движение (вне сферы действия специальной теории), во всем вышеперечисленном могут возникнуть сомнения.

Допустим, два корабля движутся бок о бок на равной скорости. Члены экипажа на каждом корабле могут считать и себя, и другой корабль находящимися в покое. Затем внезапно корабль Y начинает двигаться вперед по отношению к кораблю X.

Экипаж корабля X может утверждать, что они были все еще в покое, пока корабль X начал двигаться вперед с ускорением. Экипаж корабля Y,  однако, может, напротив, утверждать, что они все еще были в покое, когда корабль X  начал двигаться назад с ускорением. Так есть ли способ выбрать одно из этих противоречащих друг другу наблюдений?

В случае такого неоднородного движения — может быть. Так, если бы корабль Y «действительно» ускорялся вперед, то люди в нем чувствовали бы, как инерция вдавливает их назад (как вас вдавливает в спинку кресла, когда вы жмете на педаль газа, сидя в своем автомобиле). С другой стороны, если бы корабль X  двигался с ускорением назад, то люди в нем чувствовали бы, как инерция отбрасывает их вперед (как вас толкает в ветровое стекло, когда вы нажимаете на тормоза). Следовательно, экипажи кораблей могли решить, который из кораблей «действительно» двигался, по тому, какую инерцию члены экипажей испытывали.

Наверное, можно определить абсолютное движение по факту и силе эффектов инерции. В своей общей теории относительности Эйнштейн перечислил, какие качества должна проявить Вселенная, чтобы таким образом нельзя было определить абсолютность движения.

Ньютоновский взгляд на массу описывал в общем-то два вида массы. По второму закону Ньютона масса определяется через инерцию, имеющуюся у тела. Это «масса инерции». Также массу можно определить через силу вызываемого им инерционного поля. Это «масса гравитации». Со времен Ньютона считалось, что эти две массы полностью идентичны, но способа доказать это не предвиделось. Эйнштейн не пытался это доказать; он просто предположил, что масса инерции и масса гравитации идентичны, и дальше уже исходил из этого допущения.

Тогда стало возможным утверждать, что и гравитация, и инерция не принадлежат отдельным телам, а являются следствием взаимодействия масс этих тел с массой всей остальной Вселенной.

Если космический корабль начинает с ускорением двигаться вперед, члены экипажа чувствуют давление инерции, вдавливающее их в корму. Но предположим, что члены команды корабля настаивают, что они оставались в покое. Тогда они объяснят, что их наблюдения за Вселенной говорят о том, что звезды и галактики за бортом корабля с ускорением движутся назад. Ускоряющееся движение назад далеких тел Вселенной тянет назад и членов экипажа, оказывая на них инерционное воздействие, в точности как было бы, если бы Вселенная находилась в покое, а корабль с ускорением двигался вперед.

Короче, воздействие инерции не может служить доказательством того, что корабль «действительно» ускоряется. Ведь тот же самый эффект наблюдался бы, если бы ускорение получил не он, а вся остальная Вселенная. Эти инерционные эффекты могут демонстрировать только относительное  неоднородное движение: или неоднородное движение корабля относительно Вселенной, или неоднородное движение Вселенной относительно корабля. Способа выяснить, какое из этих двух движений «реально», не существует.

Можно также задать вопрос, «действительно» ли Земля вращается. Большую часть человеческой истории Земля считалась неподвижной, поскольку казалась неподвижной. После того как было проделано много интеллектуальной работы, ее вращение было продемонстрировано к удовлетворению всех ученых и тех неученых, кто внял аргументам или готов был прислушаться к мнению авторитетов. Но вращается ли она «на самом деле»?

Один из аргументов в пользу вращения Земли основывается на том, что она растянута по линии экватора. Это объясняется эффектом центрифуги, который имеет в своей основе вращение. Если бы Земля не вращалась, не было бы эффекта центрифуги и Земля не была бы растянута в плоскости экватора. Именно существованием этого растяжения часто доказывают «реальность» вращения Земли.

К этому аргументу стоило бы прислушаться, если бы Земля была во Вселенной одинока, но ведь это не так. Если посчитать Землю неподвижной, то можно было сказать, что это Вселенная со всей своей огромной массой быстро вращается вокруг Земли. Воздействие этой огромной вращающейся массы приводит к растягиванию Земли в плоскости экватора — точно так же, как если бы Земля вращалась, а Вселенная была бы неподвижна. Все эффекты вращения можно с одинаковой уверенностью объяснять в любой системе отсчета.

Можно также утверждать, что если бы Земля была неподвижна, а вся остальная Вселенная вращалась бы вокруг нее, то далекие звезды, для того чтобы двигаться по своим гигантским орбитам, преодолевая их всего за 24 часа, должны двигаться со скоростью во много раз выше световой. Из этого можно сделать вывод, что вращение Вселенной вокруг Земли невозможно, а следовательно, «действительно» вращается Земля, а не Вселенная. Однако если рассматривать Вселенную как вращающуюся вокруг Земли, а далекие звезды — движущимися на больших скоростях, то сокращение Фитцджеральда уменьшит расстояния, которые им приходится преодолевать до таких, на которых их скорости будут меньше скорости света.

Конечно, может возникнуть вопрос, что вряд ли разумно предполагать, что вся Вселенная вращается вокруг Земли, — гораздо естественнее представить себе, что это вращение Земли приводит к кажущемуся вращению Вселенной. Таким же образом, гораздо разумнее считать, что это космический корабль движется с ускорением вперед, чем что вся Вселенная движется с ускорением назад мимо одного неподвижного корабля.

Это совершенно верно и проще принять за данность, что это именно Земля вращается (или что это именно корабль движется), и астрономы будут продолжать настаивать на этом, несмотря на догматы относительности. Однако теория относительности не утверждает, что одна система отсчета не может быть проще или полезнее, чем другая, а лишь то, что одна система отсчета не более правомочна,  чем любая другая.

Представим, что иногда Земля считается неподвижной только потому, что так проще. Бросая мяч, бейсболист никогда не думает о вращении Земли. Поскольку и он сам, и мяч, и игрок с битой, ждущий мяча, все вместе движутся вместе с Землей, как бы она ни двигалась, то для подающего проще считать Землю неподвижной и рассчитывать силу и направление броска, исходя из этого. Для него система отсчета с неподвижной Землей полезнее, чем система отсчета с вращающейся Землей, но это не делает систему отсчета с неподвижной Землей более правомочной.

 

 

Гравитация

 

В своей общей теории Эйнштейн обновил и концепцию гравитации. Ньютон считал, что раз Земля вращается вокруг Солнца, то между ними должна существовать сила взаимного притяжения. Эйнштейн же показал, что вращение Земли вокруг Солнца можно объяснить через геометрию пространства.

Представим аналогию. Подающий посылает мяч для гольфа катиться по лужайке по направлению к лунке. Мяч ударяется о край лунки и падает в нее. Однако, если он движется слишком быстро, он прокрутится вдоль стенки лунки и выкатится с другой стороны в новом направлении. Он немного покружился вокруг середины лунки, но никто же не предположит на основе этого, что между мячом и серединой лунки есть сила притяжения.

Давайте представим совершенно ровную, лишенную трения поверхность бесконечной протяженности. Мяч, по которому ударяет клюшка, будет вечно катиться по ровной прямой линии.

Но что, если покрытие неровно, если на нем есть кочки и ямки? Траектория мяча, прокатившегося по краю кочки, будет искривлена по направлению от центра ямки. Траектория мяча, прокатившегося по краю ямки, будет искривлена по направлению к центру ямки. Если ямки и кочки по какой-то причине невидимы и обнаружить их невозможно, то нас могут озадачить случайные отклонения шаров от прямолинейного движения. Мы может предположить, что существуют невидимые силы притяжения или отталкивания, толкающие шар туда и сюда.

Предположим, на такой лужайке есть конусообразная ямка с крутыми стенами. Тогда можно представить, что мяч для гольфа принимает замкнутую орбиту по стенкам этой воронки, как бобслей, бесконечно кружащийся по округлой насыпи. Если бы имелось трение, кружащийся шар терял бы кинетическую энергию и мало-помалу упал бы на дно воронки. В отсутствие трения он будет сохранять свою орбиту.

Эйнштейновское понятие о гравитации представляет очень похожую картину. Пространство-время имело бы здесь четырехмерную аналогию плоской лужайки, если бы оно было свободно от материи. Материя же, однако, производит «ямки»; чем более массивна материя, тем глубже «ямка». Земля движется вокруг Солнца, как будто она кружится по краю углубления. Если бы в космосе было трение, она бы медленно сдвигалась к центру «ямки» (то есть по спирали падала бы на Солнце).

В отсутствие трения она неопределенно долго сохраняет свою орбиту. Эллипс, по которому движется Земля, демонстрирует, что ее орбита по краю «углубления» не является совершенно ровной по плоскости четырехмерной площадки (иначе орбита была бы круговой). Небольшой наклон орбиты приводит к небольшой эллиптичности, а больший наклон — к большей эллиптичности. Именно эти «ямки», производимые присутствием материи, привели к понятию об искривленном пространстве.

Выводы из специальной теории относительности, например увеличение массы при движении и эквивалентность массы и энергии, были продемонстрированы без труда. Доказать же действительность общей теории оказалось гораздо труднее. Гравитация, рассматриваемая по Эйнштейну, производит результаты, столь похожие на ту гравитацию, какой ее видел Ньютон, что хочется посчитать обе теории равнозначными, а затем выбрать ту, что проще и больше соответствует «здравому смыслу», а это конечно же ньютоновская.

Однако есть области, где выводы из представлений Эйнштейна действительно несколько отличались от предполагаемых по теории Ньютона. Изучающий эти выводы должен будет выбирать между этими двумя теориями, найдя для этого более удовлетворительную причину, чем простота. Первая из таких областей касается планеты Меркурий.

Различные тела Солнечной системы, по представлениям Ньютона, движутся в соответствии с силами гравитации, которым они подвергаются. Каждое тело подвергается силе притяжения со стороны всех других тел во Вселенной, так что точно и полностью рассчитать движения любого тела вряд ли возможно. Однако в Солнечной системе сильнее всего воздействует гравитационное поле Солнца. Гравитационные поля нескольких других тел, находящихся близко к рассматриваемому телу, тоже имеют значение, но оно невелико.

Если учесть и их, то движение планет Солнечной системы может быть объяснено с достаточной степенью точности. Если, несмотря на это, все же существуют расхождения между рассчитанным и реальным движением, остается допустить, что имеется еще какое-то неучтенное гравитационное воздействие.

Например, присутствие расхождений в орбите Урана привело к поиску упущенного гравитационного воздействия и к открытию в середине XIX века планеты Нептун.

Во время открытия Нептуна изучалось также расхождение в движении Меркурия, ближайшей к Солнцу планеты. Как и другие планеты, Меркурий движется по эллиптической орбите вокруг Солнца, где Солнце находится в одном из фокусов эллипса. Это означает, что планета не всегда находится на одном расстоянии от Солнца. На его орбите есть точка, в которой он наиболее близок к Солнцу, — перигелий,  и точка на противоположном конце орбиты, на которой он наиболее далек от Солнца, — афелий.  Соединяющая их линия называется главной осью.  Меркурий не повторяет своей орбиты в точности, но двигается таким образом, что орбита получается как бы в форме розетки, и главная ось эллипса медленно вращается.

Это могло бы быть объяснено влиянием гравитации ближайших к Меркурию планет, но не полностью. После того как были приняты во внимание все известные гравитационные воздействия, угол, на который действительно поворачивалась главная ось (и две ее крайние точки — перигелий и афелий), оставался чуть больше, чем должен был бы быть, — больше на 43,03 секунды за столетие. Это означало, что главная ось орбиты Меркурия делала полный — и необъяснимый — поворот за 3 000 000 лет.

Леверье, один из первооткрывателей Нептуна, предположил, что между Меркурием и Солнцем находится неоткрытая планета и что воздействие гравитации этой планеты на Меркурий могло привести к этому дополнительному движению перигелия. Однако планета так и не была обнаружена, и, даже если бы она существовала (или если бы пояс планетоидов равной массы существовал бы вблизи Солнца), гравитационное воздействие оказывалось бы также на Венеру, а этого не было обнаружено.

Ситуация оставалась загадочной еще семьдесят лет, пока Эйнштейн в 1915 году не объявил, что общая теория относительности изменила взгляд на гравитацию ровно настолько, чтобы ввести дополнительный фактор, который мог бы просчитать необъяснимую часть движения перигелия Меркурия. (Должно иметь место такое же, но гораздо более слабое воздействие на планеты, находящиеся дальше от Солнца, — слишком маленькое, чтобы его можно было точно определить.)

Эйнштейн также предсказал, что гравитация должна влиять на лучи света, что отсутствовало в ньютоновских воззрениях. Свет звезд, проходящий очень близко от Солнца, например, подвергался бы влиянию геометрии пространства и изгибался бы по направлению к центру Солнца. Наши глаза следовали бы за лучом света, мысленно продолжая его новое направление, и мы видели бы звезду дальше от центра Солнца, чем она находится на самом деле. Это воздействие очень мало. Даже если свет проходил у самого края Солнца, видимое положение звезды сдвигалось бы всего на 1,75 секунды, а если свет проходил дальше от Солнца, сдвиг положения звезды был бы еще меньше.

Конечно, свет звезд, проходящий около Солнца, нельзя наблюдать обычным путем, разве что на протяжении нескольких минут во время полного затмения. В то время, когда была опубликована общая теория, шла Первая мировая война и ничего нельзя было сделать. Однако в 1919 году война была окончена и можно было наблюдать полное затмение с острова Принцип в Гвинейском заливе у берегов Западной Африки. Под британским покровительством на остров была выслана исследовательская экспедиция со специальной целью — проверить общую теорию.

Исследователи замерили положение близких к Солнцу звезд и сравнили с их положением полгода спустя, когда Солнце находилось на другом конце неба. Результаты исследований подтвердили общую теорию.

В конце концов теория Эйнштейна предсказала, что свет должен терять энергию, если он движется против гравитации, и приобретать ее, если «падает», так же как и любой обычный предмет; у предмета, например у мяча, эта потеря энергии будет выражаться в потере скорости. Однако свет может двигаться только с одной скоростью; следовательно, потеря энергии будет выражаться у него в уменьшении частоты и увеличении длины волны. Так, исходя из звезды, свет будет подвергаться небольшому «красному смещению» по мере потери энергии. Но это воздействие так мало, что его нельзя измерить.

Однако недавно были обнаружены такие звезды (белые карлики),  которые обладают невероятной плотностью и гравитационное поле которых в тысячи раз сильнее, чем поле обычных звезд. Покидая такую звезду, свет теряет достаточно энергии, чтобы его спектральные линии демонстрировали отчетливое красное смещение. В 1925 году американский астроном Уолтер Сидни Адамс (1876–1956) смог изучить спектр белого карлика — звезды, парной звезде Синус, и подтвердить это предсказание Эйнштейна.

Общая теория относительности, таким образом, одержала три победы над прежними воззрениями на гравитацию, но все это были астрономические победы. Только в 1960 году общая теория была привнесена в лабораторную работу.

Ключ к этой лабораторной демонстрации обнаружил в 1958 году немецкий физик Рудольф Людвиг Моссбауэр (р. 1929), показавший, что при определенных обстоятельствах можно сделать кристалл, испускающий пучок гамма-лучей[96] одинаковой длины волны. Гамма-лучи такой длины волны могут поглощаться кристаллом, похожим на тот, которым были произведены. Если гамма-лучи имеют хоть немного отличную длину волны, они не будут поглощаться. Это называется эффектом Моссбауэра.

Итак, если такой пучок гамма-лучей испускается вниз так, что он «падает» по направлению гравитации, он набирает энергию и длина его волны становится короче — если общая теория относительности верна. Падая всего лишь на сотню футов, он должен набрать достаточно энергии, чтобы длина волны гамма-лучей уменьшилась, хотя и очень незначительно, но достаточно для того, чтобы второй кристалл уже не поглощал этот пучок.

Более того, если испускающий гамма-лучи кристалл движется вверх во время испускания, то длина волны гамма-луча возрастает благодаря эффекту Допплера — Физо. Скорость, с которой кристалл движется вверх, может быть настроена ровно таким образом, чтобы нейтрализовать воздействие гравитации на падающий гамма-луч. Тогда гамма-луч опять будет поглощен кристаллом. Проводившиеся в 1960 году эксперименты с большой точностью подтвердили общую теорию относительности, но это была еще не самая впечатляющая демонстрация ее верности.

Неудивительно, что релятивистский взгляд на Вселенную теперь является общепринятым (по крайней мере, до следующего уточнения) среди физиков всего мира.

 

Глава 8.

КВАНТЫ

 

Излучение черного тела

 

Теория относительности не отрицает существования эфира. Однако она устраняет необходимость в нем, а если он не нужен, зачем о нем думать?

Так, отпадает необходимость в эфире как в мериле абсолютного движения, поскольку релятивизм начал с утверждения о том, что такого абсолютного мерила не существует, и закончил демонстрацией отсутствия его необходимости. И опять же эфир не является необходимым в качестве среды для передачи силы гравитации и обеспечения «воздействия на расстоянии». Если гравитация — вопрос геометрии пространства-времени, а не передаваемая сила, то вопрос о возможности воздействия на расстоянии не встает.

Остается еще одно возможное использование для эфира — как среды, в которой передаются световые волны через вакуум. Вторая работа Эйнштейна, изданная в 1905 году (в добавление к его статье о специальной относительности), устранила и эту возможность. Работа Эйнштейна по относительности развилась из парадокса, затрагивающего свет, который проявился в ходе эксперимента Михельсона — Морли (см. гл. 6). Вторая статья Эйнштейна развилась из другого парадокса, также имеющего дело со светом, который возник в последних десятилетиях XIX века (именно за свою вторую статью он позже получил Нобелевскую премию).

Этот второй парадокс начался с работы Кирхгофа по спектроскопии (см. гл. 4). Он показал, что вещество, впитывавшее определенные частоты света лучше, чем остальные, будет также и испускать эти же частоты лучше при нагревании до раскаленного состояния.

Тогда предположим, что кто-либо представил вещество, способное поглощать весь свет всех частот, который падает на него. Такое тело не будет отражать света никакой частоты и соответственно будет совершенно черным. Поэтому естественно называть такое вещество черным телом.  Если черное тело раскалить, то, по правилу Кирхгофа, его испускание должно быть таким же совершенным, как и его поглощение. Оно должно испускать свет всех частот, поскольку оно поглощает все частоты.

Работа Кирхгофа должна была удовлетворить интерес физиков к количественным аспектам излучения и к тому, как такое излучение изменялось в зависимости от температуры. Общеизвестно было, что излучаемая телом энергия возрастает по мере его нагревания, но количественно это было измерено только в 1879 году австрийским физиком Йозефом Стефаном (1835–1893). Он показал, что вся излучаемая телом энергия возрастает пропорционально четвертой степени разницы в абсолютной температуре. (Абсолютная температура, обозначаемая °К, равна температуре по Цельсию, °С, плюс 273°; см. ч. I.)

Представим себе, к примеру, что при комнатной температуре, 300 °К, тело излучает определенное количество энергии. Если температура поднимается до 600 °К — температуры плавления свинца, — абсолютная температура удваивается и общее количество излучаемой энергии возрастает в 24 то есть в 16 раз. Если то же самое тело нагреть до температуры 6000 °К, какова она на поверхности Солнца, это в двадцать раз большая температура, чем комнатная, и излучает оно в 204, или в 160 000 раз больше энергии.

В 1884 году Больцман (один из разработчиков кинетической теории газов) дал этому открытию твердое математическое обоснование и показал, что оно точно относится только к черным телам и что нечерные тела всегда излучают меньше тепла, чем полагается по закону Стефана. Поэтому такое отношение иногда называют законом Стефана — Больцмана.

Но с увеличением температуры меняется не только общее количество энергии. Природа испускаемых«волн тоже меняется, и это известно человеку. Для предметов с температурой батарей парового отопления, например (менее 400 °К), испускаемое излучение лежит в спектре низкочастотного инфракрасного. Ваша кожа поглощает инфракрасное излучение, и вы ощущаете его как тепло, но вы ничего не видите. Батарея в темной комнате не видна.

По мере повышения температуры предмета он не только излучает больше тепла, но и частота излучения тоже как-то меняется. К тому моменту, когда температура поднимается до 950 °К, тело уже достаточно излучает высоких частот, чтобы воздействовать на сетчатку и чтобы приобретать в наших глазах тусклый красный свет. По мере того как температура еще повышается, красный свет делается еще ярче и в конце концов становится оранжевым, потом — желтым, поскольку испускается все больше и больше света все более высоких частот.

При температуре 2000 °К предмет, уже ярко светящийся, все еще испускает много излучения в инфракрасном спектре. Только когда температура достигает 6000 °К, температуры поверхности Солнца, тогда большая часть испускаемого излучения лежит в видимой части спектра. (На самом деле, скорее всего, именно потому, что поверхность Солнца имеет определенную температуру, наши глаза и сформировались таким образом, чтобы быть чувствительными именно к этой части спектра.)

Вплоть до конца XIX века физики пытались измерить распределение излучения среди света различных частот на различных температурах. Для того чтобы сделать это точно, требовалось черное тело, поскольку только тогда можно было быть уверенным, что на каждой частоте излучается весь возможный при данной температуре свет. Для нечерного тела определенные частоты с большой долей вероятности должны были излучаться недостаточным образом; точное положение этих частот зависело от химической природы излучающего тела.

Поскольку ни одно существующее тело не поглощает всего света, падающего на него, то ни одно реальное тело не является полностью черным телом, что казалось серьезным затруднением на пути этого направления исследований. Однако в 90-х годах XIX века немецкий физик Вильгельм Вин (1864–1928) придумал оригинальный способ обойти это препятствие.

Представим себе поверхность с отверстием. Свет с любой длиной волны, попадая в это отверстие, упадет на грубую внутреннюю стену и будет большей частью поглощен. То, что не будет поглощено, будет рассеяно во всех направлениях, так что попадет на другие стены и будет поглощено там. При каждом контакте со стеной будет происходить дополнительное поглощение, и только крошечная часть света сможет отражаться достаточно долго, чтобы в конце концов снова отразиться из отверстия. Соответственно это отверстие будет выполнять роль совершенного поглотителя (в пределах разумного) и, следовательно, будет представлять собой черное тело. Если поверхность нагреть до определенной температуры и оставить таковой, то излучение, испускаемое из отверстия, будет являться излучением черного тела  и распределение его частоты можно изучать.

В 1895 году Вьен произвел такое исследование и обнаружил, что при заданной температуре энергия излучалась на определенных частотах, увеличиваясь с возрастанием частоты и достигая максимума, а затем начинала уменьшаться, по мере того как частота поднималась еще выше.

Повышая температуру, Вьен обнаруживал, что на каждой частоте излучается больше энергии и что снова достигается максимум. Однако новый максимум был на большей частоте, чем предыдущий. Фактически, по мере того как он продолжал поднимать температуру, максимум частоты излучения продолжал двигаться в направлении все более и более высоких частот. Значение максимума частоты изменялось напрямую вместе с абсолютной температурой (T), так что закон Вьена  можно выразить следующим образом:

 

Vmax = kT. (Уравнение 8.1)

 

где k  — это константа отношения.

И закон Стефана, и закон Вьена очень важны для астрономии. Из природы спектра звезды можно узнать величину температуры ее поверхности. А из него можно получить представление о степени, в которой она излучает энергию, и, следовательно, о времени ее жизни. Чем горячее звезда, тем более короткой будет ее жизнь.

Из закона Вьена следует, что цвет звезд определяется их температурой (а не приближением или удалением их от нас, как предполагал Допплер, — см. гл. 5). Красноватые звезды сравнительно холодные, температура их поверхности 2000–3000 °К. Оранжевые звезды имеют температуру поверхности 3000–5000 °К, а желтые (такие, как наше Солнце) — 5000–8000 °К. Есть еще белые звезды, температура поверхности которых 8000–12 000 °К, а голубоватые звезды еще горячее.

 

 

Постоянная Планка

 

Тут возникает парадокс, поскольку остается загадкой, почему излучение черного тела должно распространяться именно так, как наблюдал Вьен. В 90-х годах XIX века физики считали, что излучающее тело случайным образом выбирает частоту, на которой излучает. Высокочастотное излучение предоставляет гораздо больший выбор, чем низкочастотное (так же как гораздо больше больших целых положительных чисел, чем малых), и, если бы излучение выбиралось случайным образом, гораздо чаще выбирались бы высокие частоты, чем низкие.

Лорд Рейлиф разработал уравнение, основанное на допущении, что все частоты могут быть излучаемыми с равной вероятностью. Он обнаружил, что количество энергии, излучаемой на определенном спектре частот, изменяется пропорционально четвертой степени частоты. Свет фиолетовой волны должен излучать в 16 раз больше энергии, чем свет красной волны, а в ультрафиолете должно излучаться еще больше. Фактически, по формуле Рейлифа, почти вся энергия излучающего тела будет излучаться очень быстро в глубоком ультрафиолете. Некоторые называли это «фиолетовой катастрофой».

Однако самым интересным касательно фиолетовой катастрофы стало то, что ее так и не произошло. Если быть точным, на самых низких частотах уравнение Рейлифа соответствовало истине и количество излучения быстро возрастало. Но вскоре количество излучения начало быстро падать по отношению к ожидаемому. Оно достигло максимума на некоей средней частоте, хотя этот максимум и был гораздо ниже ожидаемого по уравнению Рейлифа, а затем на еще более высоких частотах количество излучения начало быстро уменьшаться, в то время как формула Рейлифа прогнозировала постоянное увеличение.

С другой стороны, Вьен разработал уравнение, которое должно было отражать то, что действительно наблюдалось на высоких частотах. К сожалению, оно не совпадало с реальностью на низких частотах.

В 1899 году немецкий физик Макс Карл Эрнст Людвиг Планк (1858–1947) взялся за решение этой проблемы. Анализ Рейлифа, как показалось Планку, был математически и логически верен при условии принятия его аксиом, а поскольку уравнение Рейлифа не соответствовало фактам, необходимо было проверить аксиомы. Что, если не все частоты излучаемы с одинаковой вероятностью? Поскольку аксиома об одинаковой вероятности требовала, чтобы излучалось все больше и больше света на все более и более высоких частотах, в то время как наблюдения показывали обратное, Планк предположил, что вероятность излучения уменьшалась с увеличением частоты.

Так, на распространение излучения черного тела будут влиять два фактора. Во-первых, непреложный факт того, что высоких частот больше, чем низких, следовательно, должна иметь место тенденция излучать больше высокочастотного, чем низкочастотного света. Во-вторых, поскольку вероятность излучения уменьшается по мере повышения частоты, должна иметься тенденция излучать меньше в высокочастотной части спектра.

На самых низких частотах, где вероятность излучения довольно высока, первый фактор доминирует и излучение увеличивается с повышением частоты, в соответствии с формулой Рейлифа. Однако по мере дальнейшего возрастания частоты большее значение приобретает второй эффект. Все большее число высоких частот более чем уравновешивается все меньшей вероятностью излучения на столь высоких частотах. Количество излучения начинает прибавляться все медленнее по мере продолжения увеличения частоты, достигает максимума, а затем начинает уменьшаться.

Предположим, что температура повышается. Это не отменит первого фактора, поскольку тот факт, что высоких частот больше, чем низких, оспариванию не подлежит. Однако что, если подъем температуры увеличивает вероятность излучения на более высоких частотах? Тогда второй фактор может быть ослабленным. В этом случае излучение (при более высоких температурах) будет продолжать увеличиваться на более высоких частотах еще долгое время до того, как этот фактор будет преодолен и подавлен ослабленным вторым фактором. Максимум излучения, следовательно, сдвинется в более и более высокие частоты по мере повышения температуры. Именно это и наблюдал Вьен.

Но как рассчитать закономерность, по которой вероятность излучения понижается по мере повышения частоты? Планк предположил, что энергия не течет непрерывно (что физики считали само собой разумеющимся), а состоит из отдельных частиц. Другими словами, Планк представил, что существуют «атомы энергии» и что излучающее тело может отдать один атом энергии или два атома энергии, но никогда не пол-атома энергии, и в любом случае излучаться должно целое число таких атомов. Более того, Планк пришел к предположению, что содержание энергии в таком атоме энергии должно зависеть напрямую от частоты света, на которой он излучается.

Планк назвал эти атомы энергии квантами  (от латинского «сколько?»), поскольку под критическим вопросом оставался размер кванта.

Представим себе выводы из этой квантовой теории.  Фиолетовый свет, частота которого в два раза больше частоты красного, должен будет излучать кванты в два раза большие, чем красный. Ни один квант фиолетового цвета не может быть излучен, пока не наберется достаточно энергии до полного кванта, поскольку меньше энергии, чем квант, по утверждениям Планка, излучать нельзя. Однако оставалась вероятность, что до того, как наполнить квант фиолетового света, набиралось достаточно энергии, часть ее могла оторваться, чтобы сформировать квант красного света, в два раза меньшего размера.

Чем выше частота света, тем меньше вероятность того, что успеет собраться достаточно энергии, чтобы сформировать полный квант до того, как он оторвется для формирования требующего меньше энергии кванта меньшей частоты. Это объясняет, почему «фиолетовой катастрофы» не случилось и почему свет излучается по большей части на низких частотах и медленнее, чем можно было бы ожидать.

С повышением температуры общее количество энергии, доступной для излучения, возрастает пропорционально четвертой степени абсолютной температуры. В таком возрастающем потоке излучения будет все более и более вероятным, что кванты более высокочастотного света будут успевать сформироваться. Таким образом, как утверждал Планк, будет возрастать вероятность излучения на высоких частотах и максимум излучения будет сдвигаться в направлении более высоких частот. При температурах в 6000 °K максимум будет лежать в видимой части спектра, хотя еще и тогда большие кванты ультрафиолета будут формироваться в небольших количествах.

Если энергетическое содержание (e) кванта излучения пропорционально частоте этого излучения (ν), то можно сказать, что:

 

e = hν,  (Уравнение 8.2)

 

где h  — константа отношения, обычно именуемая постоянной Планка.  Если мы решим уравнение 8.2 для h, мы увидим, что h = e/ν.  Поскольку единицы измерения e  в системе СГС — эрги, a ν —  обращенные секунды (1/секунды), то единицы измерения И —  эрги, деленные на обращенную секунду, то есть эрги, умноженные на секунду, или «эрго-секунды». Энергия, умноженная на время, и есть то, что физики называют действием.  Соответственно можно сказать, что размерность постоянной Планка — единицы измерения действия.

Планк получил уравнение, содержащее h, такое, что, с его помощью, как он обнаружил, можно описать распространение излучения черного тела, соответствующее наблюдаемому, на широком промежутке частот. В конце концов он сделал это, придав А соответствующее, очень малое значение. Самое точное современное значение h —  0,0000000000000000000000000066 256 эрго-секунд, или 6,6256∙10–27 эрго-секунд.

Чтобы понять, что это значит, давайте представим, что оранжевый свет с длиной волны 6000 Å имеет частоту 50 000 000 000 000 000, или 5∙1016 колебаний в секунду. Если умножить это на постоянную Планка, мы увидим, что энергетическое содержание кванта оранжевого света — 5∙1016 x 6,6256.10– 27,  или около 3,3–10 эрга. Это примерно три миллиардных эрга, а сам эрг — лишь маленькая единица измерения энергии.

Неудивительно, что до Планка отдельные кванты излучаемой энергии не наблюдались.

Квантовая теория Планка, о которой было объявлено в 1900 году, оказалась водоразделом в истории физики. Все физические теории, не рассматривавшие кванты, а считавшие энергию постоянной, иногда объединяют в группу классической физики,  в то время как физические теории, рассматривающие кванты, считают современной физикой,  а 1900 год является удобной точкой раздела.

Но в свое время теория Планка особого шума не вызвала. Сам Планк не видел для нее другого применения, кроме описания того, как распределяется излучение черного тела, и физики были не готовы настолько радикально изменить свои воззрения на энергию только для того, чтобы одержать эту конкретную победу. Сам Планк и то колебался и временами пытался обрисовать свою квантовую теорию таким образом, чтобы она была как можно ближе к классическим воззрениям, предполагая, что энергия принимает форму квантов, только будучи излучаемой, и что поглощается она сплошным потоком.

И снова, оглядываясь назад, мы можем увидеть, что кванты могли бы объяснить множество фактов о поглощении света, которые не в силах объяснить классическая физика. Во времена Планка было хорошо известно, что фиолетовый свет гораздо действеннее, чем красный, производит химические реакции и что ультрафиолетовый свет еще действеннее в этом плане. Прекрасным примером была фотография, поскольку фотопленка, которую использовали в XIX веке, была очень чувствительна к фиолетовому краю спектра и довольно нечувствительна к красному.

На самом деле ультрафиолетовый свет был открыт за столетие до Планка по его явному воздействию на нитрат серебра (см. гл. 5). Разве не закономерно было бы предположить, что большие кванты ультрафиолетового света могут производить химические реакции с большей легкостью, чем маленькие кванты красного света? И разве нельзя сказать, что картина только прояснится, если посчитать, что энергия поглощается только целыми квантами?

Однако этот аргумент не был использован для того, чтобы квантовая теория стала применяться к поглощению. Вместо этого Эйнштейн использовал похожий аргумент в связи с открытым позже еще более впечатляющим явлением.

 

 

Фотоэлектрический эффект

 

За два последних десятилетия XIX века было обнаружено, что некоторые металлы ведут себя так, как будто отдают электричество под воздействием света. В то время физики начали понимать, что электричество связано с движением субатомных частиц, именуемых электронами,  и что воздействие света заключается в том, что он приводил к испусканию электронов из металлических поверхностей. Это фотоэлектрический эффект.

При дальнейшем изучении фотоэлектрический эффект предстал полной загадкой. Казалось очевидным, что в обычных условиях электроны закреплены в структуре металла и что для того, чтобы разорвать это закрепление и высвободить электроны, требуется затратить определенное количество энергии. Еще казалось, что по мере увеличения интенсивности света все больше и больше энергии передавалось металлической поверхности. Тогда электроны не только высвобождаются, но и вылетают с огромной скоростью. Чем интенсивнее свет, тем больше скорость. Представлялось, что частота света не влияет на этот эффект и важна только общая энергия света, каковой бы ни была его интенсивность.

Так казалось, но было не так.

Немецкий физик Филипп Ленард (1862–1947) после тщательного исследования в 1902 году обнаружил, что для каждой поверхности, на которой обнаруживался фотоэлектрический эффект, имелась ограничительная пороговая частота,  выше которой, и только выше которой наблюдался эффект.

Предположим, например, что для конкретной поверхности эта пороговая частота — 500 квадриллионов колебаний в секунду (это частота оранжевого света с длиной волны 6000 Å). Если свет меньшей частоты, например красный свет 420 квадриллионов колебаний в секунду, падает на такую поверхность, ничего не происходит. Электроны не выпускаются. Не важно, насколько ярок или интенсивен свет и сколько энергии в нем содержится, — электроны не испускаются.

Однако, если частоту света поднять до 500 квадриллионов колебаний в секунду, электроны начинают испускаться, но практически лишенными кинетической энергии. Как будто полученной ими из света энергии только-только хватило, чтобы разорвать силу, удерживающую их на поверхности, но уже не хватило на то, чтобы снабдить их еще и кинетической энергией. Ленард обнаружил, что повышение интенсивности света на этой пороговой частоте никоим образом не добавляло электронам кинетической энергии. В результате возросшей интенсивности больше электронов испускается с поверхности в количестве, пропорциональном энергии оранжевого света, но всем им недостает кинетической энергии.

Если частоту увеличивать еще дальше и взять фиолетовый свет в 1000 квадриллионов колебаний в секунду, электроны будут испускаться с приличным количеством кинетической энергии. Количество испускаемых электронов будет изменяться пропорционально общей энергии света, но опять же они все будут иметь одинаковую кинетическую энергию.

Другими словами, слабый фиолетовый свет приведет к испусканию немногих электронов с высокой энергией; интенсивный оранжевый свет приведет к испусканию большого количества электронов с низкой энергией, а красный свет даже чрезвычайной интенсивности вообще не приведет к испусканию электронов.

В рамках физических теорий XIX века просчитать это было невозможно, но в 1905 году Эйнштейн разработал объяснение, в котором использовалась квантовая теория Планка, которой было уже пять лет, но которая еще не получила признания.

Эйнштейн решил, что свет не только излучается в виде квантов, как установил Планк, но и поглощается в виде квантов. Когда свет падает на поверхность, электроны, закрепленные на поверхности, поглощают энергию по кванту за раз. Если энергии одного кванта оказывалось достаточно для преодоления сил, удерживающих его на поверхности, он высвобождался, иначе — нет.

Конечно, электрон может предположительно набрать достаточно энергии, чтобы оторваться и поглотить второй квант, если не хватило первого. Однако это маловероятно. Чрезмерно велика вероятность, что до того, как он успеет поглотить второй квант, он уже излучит первый. Следовательно, один квант должен проделать работу самостоятельно; если это не так, просто умножается количество квантов (которые сами по себе не могут проделать эту работу) и ничего не получается. То же самое, как если человек недостаточно силен, чтобы поднять камень в одиночку, то даже миллион человек такой же силы не смогут поднять его, подходя по очереди. Камень останется на месте.

Однако размер кванта возрастает с повышением частоты. На пороговой частоте квант является лишь достаточно большим, чтобы преодолеть силу, удерживающую электрон на конкретной поверхности. По мере того как возрастает частота (и энергетическое содержание кванта), все больше и больше энергии будет оставаться после высвобождения электрона для перевода в кинетическую энергию.

Для каждого вещества имеется отдельная характеризующая его пороговая частота, зависящая от того, насколько сильно электроны удерживаются своим веществом. Для такого металла, как цезий, в котором электроны привязаны очень слабо, пороговая частота находится в инфракрасном спектре. Даже небольшие кванты инфракрасного света несут достаточно энергии, чтобы разорвать эту слабую связь. Для такого металла, как серебро, в котором электроны держатся сильнее, пороговая частота лежит в ультрафиолетовой части спектра.

Тогда Эйнштейн предложил следующее отношение:

 

½mv2 = hν – w , (Уравнение 8.3)

 

где ½mv2 — кинетическая энергия испускаемого электрона; hν  (постоянная Планка на частоту) — энергетическое содержимое кванта, поглощаемого поверхностью; а w — энергия, требуемая для того, чтобы электрон оторвался от поверхности. На пороговой частоте электроны только-только могут отрываться и обладать кинетической энергией не будут. По этой причине уравнение 8.3 примет вид 0 = hν  — w; а это будет означать, что hν = w.  Другими словами, w  будет представлять энергию светового кванта на пороговой частоте.

Предложенное Эйнштейном объяснение фотоэлектрического эффекта было таким элегантным и так хорошо соответствовало наблюдениям, что квантовая теория внезапно обрела популярность. Изначально она была разработана для того, чтобы объяснять факты излучения, а теперь внезапно оказалось, что она без изменений может объяснять фотоэлектрический эффект — совершенно иное явление. Это больше всего впечатляло.

Еще большее впечатление это произвело в 1916 году, когда американский физик Роберт Эндрус Милликен (1868–1953) провел тщательные эксперименты, в ходе которых измерил энергию электронов, испускаемых светом различных частот, и обнаружил, что энергии, которые он измерял, в точности соответствовали уравнениям Эйнштейна. Более того, измеряя энергию электронов (½mv2), частоту используемого света (ν)  и пороговую частоту для используемой поверхности (w), он смог вывести значение h (постоянной Планка) из уравнения 8.3. Он получил значение, очень близкое к тому, которое получил Планк в своем уравнении излучения.

С 1916 года квантовая теория получила среди физиков всеобщее признание. Теперь стало принято считать, что энергия может излучаться и поглощаться только целым числом квантов и фактически что вся энергия во всех своих формах «квантизирована», то есть может рассматриваться только как состоящая из неделимых квантов. В дальнейшем из этой концепции был выдвинут самый полезный взгляд на строение атома, как мы увидим в III части этой книги.

 

 

Фотоны

 

Эйнштейн довел понятие квантов до логического завершения. Квант казался аналогичным «атому энергии», или «частице энергии», поэтому почему бы не посчитать такие частицы именно частицами? Тогда свет будет состоять из частиц, которые в конце концов назвали фотонами  (от греческого слова, означающего «свет»).

Это представление повергло физиков в шок. Волновая теория света установилась всего за 100 лет до этого и на протяжении столетия одерживали победу за победой, пока теория частиц Ньютона не была похоронена и предана полному забвению. Если же свет в конце концов состоял из частиц, то что же делать со всеми свидетельствами, которые неопровержимо говорили о его волновой природе? Что же теперь делать с экспериментами интерференции, поляризации и т. д.?

Ответ не имеет с этим ничего общего. Просто неверно считать, что объект может быть или  частицей, или  волной. Совершенно так же можно спорить и о том, что или мы находимся вверх головой, а австралийцы вниз головой, или мы вниз головой, а австралийцы — вверх. Фотон является и частицей, и волной в зависимости от точки зрения. (Некоторые физики полушутя говорят о «волночастицах».) Фактически можно выйти за рамки этого противопоставления (как я объясню в дальнейшем, в III части этой книги) и настаивать на том, что все фундаментальные единицы Вселенной одновременно являются и  волнами, и  частицами.

Трудно принять подобное утверждение, потому что почти неизбежно возникает вопрос: «Но как один и тот же объект может быть одновременно и волной и частицей?»

Проблема здесь в том, что мы автоматически рассуждаем о незнакомых объектах как о знакомых; мы описываем новые явления, говоря «атом похож на бильярдный шар», или «световые волны — это как волны на воде». Но на самом деле это значит только, что некоторые конкретные свойства атомов или световых волн напоминают аналогичные свойства бильярдных шаров или волн на воде. Не все свойства соответствуют: атом не такой большой, как бильярдный шар; световая волна не такая мокрая, как волна на воде.

У бильярдного шара есть свойства и волны, и частицы. Однако свойства частицы в нем так очевидны, а свойства волны так неприметны и неопределимы, что мы думаем о бильярдном шаре только как о частице. Волны на воде тоже имеют свойства и волны, и частицы, но именно свойства волны очевидны, а свойства частицы незаметны. Фактически все обычные предметы чрезвычайно разбалансированы в этом отношении, поэтому мы и пришли к выводу, что предмет может быть либо частицей, либо волной.

Фотоны же, из которых состоит свет, лучше уравновешены в этом отношении. В них очевидны и свойства волны, и свойства частицы. В нашем повседневном опыте сравнить их не с чем. Однако только из-за того, что мы не имеем знакомого аналога, мы не должны считать, что волночастица «противоречит здравому смыслу» или является парадоксом или, что хуже того, «ученые не смогли прийти к решению».

Мы увидим это яснее, если выберем не прямую аналогию. Представьте себе конус из твердого вещества, например из стали. Если перевернуть такой конус, выровняв его основание по линии горизонта, он покажется треугольным. Держа его таким образом, его можно пронести сквозь треугольное отверстие в стальном листе, но не сквозь круглое отверстие такой же площади.

Представим, что конус повернули острием к глазу. Теперь его граница кажется круглой. В этой ориентации он пройдет через круглое отверстие в стальном листе, но не сквозь треугольное отверстие такой же площади.

Если два наблюдателя, знакомые с двумерной плоскостной геометрией, но не с трехмерной объемной геометрией, проведут такие эксперименты, один будет с жаром настаивать, что конус треугольный, поскольку проходит сквозь треугольное отверстие, а другой будет утверждать с таким же пылом, что конус круглый, потому что проходит сквозь круглое отверстие. Они будут спорить целую вечность и не придут к выводу.

Если этим двум наблюдателям сказать, что они оба частью правы, а частью не правы и что объект их спора имеет свойства как треугольника, так и круга, их первой реакцией (в основе которой будет лежать двухмерный опыт) будет ярость — как это предмет может быть одновременно и кругом, и треугольником?

Однако конус не то чтобы являлся и кругом, и треугольником, но он имеет как круглое, так и треугольное сечения, а это означает, что часть его свойств — свойства круга, а часть — свойства треугольника.

Таким же образом фотоны в каких-то аспектах имеют свойства волны, а в каких-то — свойства частицы. Волнообразные свойства их, так красиво продемонстрированные в XIX веке, были результатом экспериментов, нацеленных на то, чтобы обнаружить волновой аспект света (как в случае правильного расположения конуса для того, чтобы показать, что он треугольный).

Частицеобразные свойства оказалось не так легко продемонстрировать. Точнее говоря, в 1901 году русский физик Петр Николаевич Лебедев (1866–1911) показал, что свет оказывает очень малое давление. Зеркало, подвешенное в вакууме на тонкой нити, реагировало на это давление, поворачиваясь и перекручивая нить. Это давление оказалось возможным измерить по небольшому закручиванию нити, происходившему в тот момент, когда луч света попадал на зеркало.

В некоторых условиях, как показал Лебедев, давление излучения оказывается более сильным, чем гравитация. Замерзшие газы, составляющие поверхность кометы, испаряются, когда комета приближается к Солнцу, и частички пыли, обычно удерживающиеся на месте замерзшим газом, освобождаются. На эти частички действуют как незначительная сила притяжения кометы, так и давление огромного солнечного излучения. Необычно большое давление излучения сильнее, чем необычно малая гравитация, и частички пыли частично сдуваются излучением, которое распространяется по всем направлениям от Солнца.

Именно так и появляется хвост кометы, состоящий из света, отраженного от этих пылинок, и всегда направленный от Солнца. Так, если комета отдаляется от Солнца, хвост движется впереди нее. Эта ориентация хвоста кометы заставила немецкого астронома Иоганна Кеплера заявить о давлении излучения за три века до того, как его существование было продемонстрировано в лаборатории.

Существование давления излучения может, как правило, служить примером частицеобразных свойств света, если мы посчитаем это давление результатом бомбардировки частицами, как давление газа (см. ч. 1). Однако в 1873 году Максвелл (который тоже работал над кинетической теорией газов) показал, что есть хорошие теоретические аргументы в пользу того факта, что световые волны могут оказывать давление излучения и как волны, а не как частицы.

Более чистый пример частицеобразных свойств был показан в 1922 году американским физиком Артуром Холли Комптоном (1892–1962). Он обнаружил, что, проникая в вещество, рентгеновский луч (это очень высокочастотная форма света, более подробно она будет обсуждаться в III томе этой книги) иногда ударял электроны и не только оказывал таким образом давление, но и сам преломлялся! При преломлении частота его несколько возрастала, а это означало, что рентгеновский луч терял энергию.

С другой стороны, электрон отскакивал в таком направлении, которое высчитывалось из преломления рентгеновского луча, и приобретал ровно столько энергии, сколько луч терял. Это преломление и переход энергии были полностью аналогичны тому, что случилось бы, если бы электрон столкнулся с электроном или, возвращаясь к сказанному, если бы бильярдный шар столкнулся с бильярдным шаром. Этот эффект Комптона  наглядно продемонстрировал, что фотон рентгеновского луча может действовать как частица.

Были хорошие причины полагать, что чем более энергичен фотон, тем более очевидными становятся его частицеобразные свойства по сравнению с волнообразными. Следовательно, эффект Комптона легче было продемонстрировать на фотоне рентгеновского луча, чем на менее энергетичных фотонах видимого света, но результат его относится ко всем фотонам. Частицеволновая природа фотонов с тех пор не подвергалась сомнению.

В то время как некоторые эксперименты освещали волнообразные свойства света, а некоторые — частицеобразные, даже не планировался эксперимент, который показал бы, что свет ведет себя одновременно и как волна, и как частица (таким же образом, конус может быть сориентирован и так, чтобы проходить сквозь треугольник, и так, чтобы проходить сквозь круг, но не так, чтобы проходить через оба отверстия). Датский физик Нильс Бор (1865–1962) установил, что придумать эксперимент, в котором свет вел бы себя одновременно и как волна, и как частица, просто невозможно в принципе. Его назвали принципом дополнительности.

Это не так страшно для ученых, как звучит. Мы привыкли определять общую форму трехмерного тела, изучая его сначала с одной стороны, затем с другой, а потом объединяя в воображении собранную таким образом информацию. Мы не стремимся видеть предмет со всех сторон одновременно и не думаем, что, только глядя со всех сторон одновременно, можно понять истинную форму предмета. Фактически, если бы мы могли его видеть со всех сторон, мы получили бы замешательство вместо просветления, как когда мы видим портрет работы Пикассо, на котором женщина нарисована одновременно и в профиль, и анфас.

Если рассматривать свет как имеющий свойства и частицы, и волны, то действительно отпадает нужда в светоносном эфире, так же как не нужен нам эфир ни для объяснения гравитации, ни в качестве мерила абсолютного движения.

Сколько бы свойств волны ни демонстрировал свет, его перемещение в вакууме делает очевидными его частицеобразные свойства. Фотоны летят сквозь бесконечные толщи вакуума точно так же, как, по описанию Ньютона, должны были лететь его менее сложные частицы.

Следовательно, когда релятивизм и квантовая теория стали общепринятыми, скажем к 1920 году, — физики перестали думать об эфире.

Но даже если считать свет состоящим из фотонов, это не отменяет того факта, что фотоны имеют волновой аспект — что-то все же колеблется. Так что же колеблется и является ли это что-то материальным?

Чтобы дать ответ на этот вопрос, давайте вспомним два явления, которые с древних времен были примерами того, что казалось воздействием на расстоянии. На это у нас уйдет несколько глав, но ответ в конце концов будет дан.

 

Глава 9.

МАГНЕТИЗМ

 

Магнитные полюса

 

Силы притяжения между телами, несомненно, наблюдались с доисторических времен, но (по крайней мере, так принято считать) первым из древних греков, кто систематически принялся за изучение сил притяжения, был Талес (640? — 546 до н.э.).

Одна из таких сил притяжения касалась железа и железной руды. Некоторые встречающиеся в природе виды железной руды (магнитный железняк), как обнаружилось, притягивали железо и, как могли заметить древние, больше ничего. Талес жил в городе Милет (на побережье Эгейского моря, ныне в Турции), и те образцы магнитного железняка, которые он изучал, предположительно были из окрестностей соседнего города Магнезии. Талес назвал его «магнезианским камнем», а притягивающие железо материалы получили соответственно название магниты,  поскольку само явление получило название магнетизм.

Талес обнаружил, что янтарь (окаменевшая смола, которую греки называли «электрон»), если его натереть, тоже излучает силу притягивания. Она отличалась от магнетической силы, поскольку магнетизм действовал только на железо, а натертый янтарь — на любой легкий предмет: пух, перья, куски сухих листьев. В поздние века были найдены и другие, кроме янтаря, предметы, которые, будучи натертыми, проявляли подобные свойства, и в 1600 году английский физик и врач Уильям Гильберт (1540–1603) предположил, что все такие объекты можно называть «электрическими» (от греческого слова, означавшего «янтарь»). Отсюда и стало к этому явлению применяться слово «электричество».

Магнетизм, хотя и более ограниченная сила, казался в тех экспериментальных условиях, которые по большей части имелись в древности и в Средние века, гораздо более сильным. Следовательно, именно магнетизм тщательно изучали две тысячи лет после Талеса.

Например, было обнаружено, что свойства магнетизма могут передаваться. Если стальной сердечник вставить в естественный магнитный железняк, он сам становится магнитом и может притягивать куски железа, хотя раньше этого не делал.

Более того, если такую намагниченную стрелку положить на пробку и пустить плавать по воде или если закрепить ее на оси так, чтобы она могла свободно вращаться, обнаружилось, что иголка не принимала любое положение случайно, а ориентировалась строго определенным образом. Эта ориентация строго приближалась к линии север — юг. И еще — если один конец намагниченной иголки пометить каким-нибудь образом, быстро становилось очевидным, что один ее конец всегда показывал на север, а другой — всегда на юг.

Поскольку концы намагниченной иголки показывали, как казалось, на полюса Земли, то начали говорить о том ее конце, что показывал на север, как о северном полюсе магнита,  а о втором — как о южном полюсе магнита.

Людям не могло не прийти в голову, что если северный полюс свободно движущейся намагниченной стрелки всегда показывает на север, то это же великолепный способ ориентироваться в пространстве! До тех пор днем ориентировались по Солнцу, ночью — по Полярной звезде, но это годилось только в хорошую погоду.

Предполагается, что китайцы использовали намагниченную стрелку в качестве указателя направления, когда пролагали пути через однообразные пустыни Средней Азии. Однако первое использование такой иголки в морских путешествиях отмечено среди европейцев в XII веке. В конце концов стрелку разместили на карте, по ободку которой были отмечены различные направления. Поскольку эти направления окружали ободок карты, намагниченная игла получила название компас  (от англ. encompass  — окружать).

Несомненно, компас принадлежит к тем простым изобретениям, которые изменили мир. Люди могли пересекать обширные океаны и без компаса (около двух тысяч лет назад полинезийцам удалось колонизировать разбросанные по Тихому океану острова без всяких компасов), но компас значительно помогал им. И не случайно именно после изобретения компаса, когда европейцы стали смело выплывать в Атлантический океан, начался «век Великих географических открытий».

К полюсам магнита железо притягивается с наибольшей силой. Если намагниченную иголку закопать в металлические опилки и потом поднять, опилки гуще всего соберутся на концах. В этом смысле магнит любой формы имеет полюса, которые можно разметить подобным образом. И полюса не образуются поодиночке. Если можно определить северный полюс, то можно определить и южный, и наоборот.

И не сложно отличить северный полюс от южного, даже не располагая магнит на карте. Предположим, что две намагниченные стрелки свободно сориентировались в направлении север-юг и что определен северный полюс каждой. Если северный полюс одного магнита поднести к южному полюсу другого, два полюса будут взаимно притягиваться и, если дать им соприкоснуться, так и будут соприкасаться. Чтобы разделить их, придется приложить силу.

С другой стороны, если северный полюс одного магнита поднести к северному полюсу другого, возникнет взаимное отталкивание магнитов. То же самое произойдет, если южный полюс одного поднести к южному полюсу другого. Если магнитам дать свободно вращаться, они развернутся и спонтанно переориентируются так, чтобы северный полюс одного смотрел на южный полюс другого. Если северный полюс одного прижать к северному полюсу другого или южный к южному, то они разделятся, как только магниты отпустят. Чтобы оставить их в контакте, потребуется приложить силу.

Итог можно подвести так: одинаковые полюса отталкиваются, разные полюса притягиваются.

Когда северный полюс магнита определен, его можно использовать для определения полюсов любого другого магнита.

Любой полюс, к которому он притягивается, — южный полюс. Любой полюс, от которого он отталкивается, — северный полюс. Впервые это было установлено в 1269 году одним из немногих экспериментаторов Средневековья французом Петером Перегринусом.

(В свете этого, наверное, правильнее было бы называть северный полюс магнита, притягиваемый Северным полюсом Земли, южным полюсом. Однако тут уже поздно что-то менять.)

Легко увидеть, что сила, исходящая из магнитного полюса, изменяется обратно пропорционально расстоянию. Если дать северному полюсу магнита приблизиться к южному полюсу другого, то можно почувствовать, как сила притяжения становится сильнее. Таким же образом, если подтолкнуть северный полюс одного магнита к северному полюсу другого, можно почувствовать, как сила отталкивания становится сильнее. Чем меньше расстояние, тем больше сила.

Конечно же мы не можем говорить отдельно о северном полюсе или южном полюсе. Каждый северный полюс сопровождается южным. Следовательно, если северный полюс магнита А притянут к южному полюсу магнита В, то южный полюс магнита А должен одновременно отталкивать южный полюс магнита В. Это, кажется, осложняет ситуацию.

Однако если использовать длинные тонкие магниты, то источник затруднений сводится к минимуму. Северный полюс магнита А близок к южному полюсу магнита В, в то время как южный полюс магнита А (на другом конце длинного куска металла) находится достаточно далеко. Создающая помехи отталкивающая сила южного полюса ослаблена из-за этого дополнительного расстояния и может быть легко проигнорирована.

В 1785 году французский физик Шарль Огюстен де Кулон (1736–1806) измерил силу между магнитными полюсами на различных расстояниях, используя для этих целей тонкие перекрученные весы. Так, если одна магнитная стрелка подвешена на тонкой нити, притяжение (или отталкивание) другого магнита к одному из полюсов подвешенной стрелки заставит подвешенную стрелку несколько перекрутиться. Сделав это, она перекрутит и нить, на которой подвешена. Нить будет сопротивляться дальнейшему перекручиванию с силой, зависящей от того, насколько она уже перекручена.

Заданная сила всегда будет производить заданное перекручивание, а из этого перекручивания можно будет высчитать и размер неизвестной силы. (Пятнадцать лет спустя Кавендиш использовал подобные весы для измерения слабых гравитационных сил, см. ч. I; а столетием позже Лебедев определял с их помощью давление света, см. гл. 8.)

Производя свои измерения, Кулон обнаружил, что магнетическая сила изменялась обратно пропорционально квадрату расстояния, как и в случае с гравитационной силой. Так, магнитная сила падала до одной четвертой от своего первоначального значения, когда расстояние возрастало вдвое, и увеличивалась в девять раз, когда расстояние сокращалось до трети своей изначальной величины. Это оставалось верным, независимо от того, рассматривалась ли сила притяжения или отталкивания.

Это может быть выражено математически следующим образом: если магнитную силу между полюсами принять за F,  силу двух полюсов за m  и m’  а расстояние между ними за d,  то:

 

F = mm'/d2.  (Уравнение 9.1)

 

Если расстояние измерять в сантиметрах, то сила будет определяться в динах (где одна дина определяется как 1 грамм на сантиметр в секунду за секунду, см. ч. I). Предположим затем, что два полюса равной интенсивности разделены расстоянием в 1 см и что сила магнитного притяжения — 1 дина. Тогда оказывается, что m  = m' , следовательно, mm'  = m2.  Тогда, раз и F  и d  взяты равными 1, то из уравнения 9.1 следует, что в этих условиях m2 = 1 и, следовательно, m  = 1.

Значит, можно говорить о полюсных единицах  как о представляющих полюса такой силы, что, будучи разделенными на 1 сантиметр, они испускают магнитную силу (притяжения или отталкивания — не важно) в 1 дину. В уравнении 9.1, где F измеряется в динах, а d —  в сантиметрах, т  и m'  измеряются в полюсных единицах.

Если магнитное поле в 5 полюсных единиц выдает силу в 10 дин на полюсную единицу в определенной точке, то интенсивность магнитной силы — 2 дины на магнитную единицу. Одна дина на магнитную единицу определяется как 1 эрстед (в честь датского физика Ханса Кристиана Эрстеда, вклад которого в изучение магнетизма будет изложен в гл. 12). Эрстед — единица измерения магнитной силы на полюсную единицу, или напряженности магнитного поля,  что обычно обозначается как H. Тогда мы можем сказать, что H = F/m,  или

 

F = mH,  (Уравнение 9.2)

 

где F —  магнитная сила, измеряемая в динах; m —  значение в полюсных единицах; Н —  магнитная напряженность в эрстедах.

 

 

Магнитные области

 

В существовании и северного, и южного полюсов и в вытекающем из этого существовании магнитного отталкивания и магнитного притяжения заключается ключевое отличие магнетизма от гравитации. Сила гравитации заключается только в притяжении, и никакой соответствующей силы гравитационного отталкивания обнаружено еще не было.

Поэтому гравитационная сила всегда максимальна, какие-либо нейтрализующие эффекты отсутствуют. Тело, имеющее массу Земли, всегда будет иметь одно и то же гравитационное притяжение независимо от своей температуры или химического состава.

С другой стороны, магнитное притяжение всегда может быть в той или иной степени нейтрализовано магнитным отталкиванием, так что магнитные воздействия будут происходить только с определенными видами материи, и то с сильно различающейся силой.

Можно ожидать (и, как мы увидим в III части этой книги, ожидание это окажется верным), что магнетизм имеет широкое распространение в природе и что магнитные силы существуют во всех видах материи. Тогда материю можно рассматривать как состоящую из микроскопических магнитов. В пользу этого воззрения (по крайней мере, в случае железа и стали) можно отнести тот давно обнаруженный факт, что если длинную намагниченную иголку поломать пополам, то обе половинки будут магнитами. Край перелома напротив первоначального северного полюса становится южным полюсом; край перелома напротив изначального южного полюса становится северным полюсом. Это будет повторяться столько раз, сколько раз сломают иголку. Легко представить, что, если первоначальную иголку разломать на микроскопические кусочки, каждый из них будет крошечным магнитом и будет иметь свой северный и южный полюса.

Эти микроскопические магниты в большинстве веществ и в большинстве условий будут сориентированы случайным образом, так что не будет (или почти не будет) концентрации на северных полюсах (или южных полюсах) в каком-либо направлении и, следовательно, магнитная сила будет обнаруживаться незначительная либо не будет обнаруживаться вовсе. Однако в некоторых встречающихся в природе веществах имеется тенденция к выстраиванию этих микроскопических магнитов, по крайней мере в какой-то мере, по линии север — юг. Тогда будет наличествовать концентрация северных полюсов в одном направлении и южных — в другом, концентрация достаточная, чтобы породить обнаруживаемое магнитное поле.

Если, скажем, северный полюс такого магнита поднести к железу, микроскопические магниты в железе сориентируются таким образом, что южные полюсы будут обращены к магниту, а северные — от него. Тогда железо и магнит будут притягиваться. Если к железу поднесут южный полюс магнита, то микроскопические магниты в железе сориентируются противоположным образом и снова появится притяжение. Поэтому каждый полюс магнита будет притягивать железо.

Когда железо находится рядом с магнитом или соприкасается с ним таким образом, что его собственные магнитные составляющие сориентированы, оно само становится магнитом. Процесс превращения железа в магнит под воздействием другого магнита называется магнитной индукцией.  Так, настриженная бумага, подвесившаяся к магниту, сама притянет другую бумажку, та — следующую и т. д. Если магнит убрать, все бумажки распадутся.

Обычно микроскопические магниты в железе сравнительно легко ориентируются под воздействием магнита и так же легко дезориентируются, когда магнит убирают. Железо обычно формирует временный магнит.  А вот если стальной брусок подвергнуть действию магнита, микроскопические магниты в стали ориентируются с большим трудом.

Однако когда магнит удаляют от стали, дезориентация происходит с таким же трудом — она достаточно затруднена, чтобы фактически вообще не происходить в обычных условиях, следовательно, сталь обычно остается постоянным магнитом.

Не только железо состоит из микроскопических магнитов, и не только железо притягивается к магниту. Другие металлы, такие как кобальт и никель (которые химически близки к железу) и гадолиний (который к нему не близок), притягиваются магнитом. Также и ряд металлических сплавов, одни из которых содержат железо, а другие — нет. Например, альнико, который, как явствует из названия, состоит из алюминия, никеля и кобальта (плюс немного меди), можно использовать, чтобы делать магниты сильнее стальных. С другой стороны, нержавеющая сталь, которая больше чем на три четверти состоит из железа, воздействию магнита не поддается.

Магнетическое вещество не обязательно должно быть металлом. Сам по себе магнитный железняк является разновидностью оксида железа, скорее почвенным, чем металлическим веществом. После Второй мировой войны был изучен целый новый класс магнитных веществ. Это ферриты, являющиеся смешанными оксидами железа и других металлов, таких как кобальт или марганец.

Материал, который демонстрирует или который можно заставить продемонстрировать сильную магнитную силу того рода, что мы привыкли видеть в обычном магните, считается ферромагнитным (от латинского слова ferrum,  что означает «железо», поскольку наиболее известным примером такого вещества является железо). Никель, кобальт, альнико, конечно, железо и сталь являются примерами ферромагнитных веществ.

Возникает вопрос, почему одни материалы ферромагнитны, а другие — нет. Если магнитные силы — свойства всей материи (а так оно и есть), почему микроскопические магниты чистой меди или чистого алюминия, например, не могут выстраиваться под воздействием имеющегося магнита? Очевидно, это выравнивание не может быть введено извне, без помощи, так сказать, самого вещества.

В ферромагнитных веществах (но даже в них только при определенных условиях) уже присутствует большая часть выравнивания в естественном состоянии. Микроскопические магниты стремятся сориентироваться параллельно миллиардами миллиардов, приводя к появлению концентраций на северном и южном полюсах то тут, то там внутри железа. Области, где таким образом сконцентрированы магнитные силы, называются магнитными областями.

Железо и другие ферромагнитные вещества состоят из таких магнитных областей, каждая из которых почти заметна. Хорошо размельченный порошок магнитного оксида железа, если его рассыпать по железу, будет проявлять тенденцию к тому, чтобы собираться на границах между смежными областями и делать их видимыми глазу.

Несмотря на присутствие этих областей, железо обычно не является магнитом. Это потому, что сами области сориентированы случайным образом, так что магнитная сила одних нейтрализуется магнитной силой соседних. Следовательно, контакт с обычным магнитом не ориентирует сами микроскопические магниты (это превыше его сил) — он просто ориентирует эти области. Так, ферромагнитный материал уже проделал почти всю работу по выравниванию и остается сделать только последний шаг для выравнивания, незначительный по сравнению с тем, что уже сделано для того, чтобы получить магнит.

Если ферромагнитное вещество разбить на части меньше отдельных составляющих его областей, то каждая такая часть будет представлять собой отдельную область или часть области. Микроскопические магниты в каждой из них будут полностью выровнены. Если такой порошок растворить в жидком пластике, области эти легко и с большой точностью могут быть выровнены под воздействием магнита в то время, когда эти частицы будут вращаться, преодолевая малое сопротивление жидкости (в отличие от гораздо большего сопротивления самого железа в твердом состоянии).

Если дать пластику затвердеть в то время, когда система все еще находится под действием магнита, области будут выровнены навсегда, и сформируется особо сильный магнит. Более того, таким магнитам можно придать любую форму и можно легко переделать в другую форму.

Все, что может нарушить выравнивание областей, ослабит или разрушит магнитную силу даже «постоянного» магнита. Если два магнита положить рядом, севером к северу и югом к югу, то магнитное отталкивание приведет к тому, что области постепенно будут отодвигаться друг от друга, — это разрушит выравнивание и ослабит магнитную силу (именно поэтому магниты всегда следует складывать севером к югу). С механической точки зрения, если магнит ударить молотком, то вибрация разрушит выравнивание и ослабит магнитную силу.

В особенности магнитные области разрушает возрастающая вибрация атомов, вызванная повышением температуры (см. ч. I). Фактически для каждого ферромагнитного вещества есть характеризующая его температура, выше которой выравнивание областей разрушается и при нагревании выше которой вещество соответственно теряет свои ферромагнитные свойства.

Впервые это было продемонстрировано французским физиком Пьером Кюри (1859–1906) в 1895 году, и поэтому пороговое значение температуры называется точкой Кюри.  Точка Кюри обычно находится ниже точки таяния жидкости, поэтому жидкости, как правило, не ферромагнитны. Например, точка Кюри для железа — 760 C°, в то время как его точка плавления — 1539 °С. Для кобальта точка Кюри сравнительно высока — 1130 °С, в то время как для гадолиния сравнительно низка — 16 °С. Гадолиний ферромагнитен только при температурах ниже комнатной. Точка Кюри может располагаться на действительно низких температурах. Для металла диспрозия ее значение около –188 °С (85 °К), так что в диспрозии области формируются только при температурах жидкого воздуха и только тогда он становится ферромагнитным.

В некоторых веществах микроскопические магниты сами собой выравниваются, но не таким образом, что северные полюса указывают все в одном направлении. Вместо этого магниты действительно выравниваются параллельным образом, но так, что в половине случаев северные полюса указывают в одном направлении, а в половине — в другом. Такие вещества называют антиферромагнитными, и из-за того, что магнитные силы одного выравнивания аннулируются магнитными силами другого, общее магнитное поле равняется нулю. Однако может оказаться, что структура вещества будет такой, что магниты с северными полюсами в одном направлении окажутся сильнее, чем магниты с северными полюсами в другом. В этом случае будет сравнительно устойчивое магнитное поле, и такие вещества называют ферримагнитными  (обратите внимание на разницу в гласной!).

Примерами ферримагнитных материалов являются ферриты. Естественно, ферримагнитный материал не может быть таким сильным магнитом, как ферромагнитный, поскольку в последнем в идеальном случае все области сориентированы в одном направлении, в то время как в первом имеет место значительная нейтрализация. Так, ферриты представляют магниты в лучшем случае в три раза слабее стального.

 

 

Земля как магнит

 

Ранних физиков сводил с ума поиск причины, по которой стрелка компаса показывает на север и юг. Некоторые выдумывали, что якобы на Крайнем Севере существует огромная железная гора, к которой притягивается намагниченная стрелка. В 1600 году английский физик Уильям Гильберт (1544–1603) поведал о целенаправленном эксперименте, который привел к более правдоподобному решению.

Стрелка компаса, вращаясь обычным образом, может вращаться только вокруг вертикальной оси и вынуждена оставаться совершенно горизонтальной. А если ее насадить на горизонтальную ось так, что условия позволили бы ей указывать вверх или вниз? Таким образом закрепленная стрелка (в Северном полушарии) действительно показывала север на несколько градусов ниже горизонта, в земле. Это назвали магнитным погружением.

Гильберт сделал шар из магнитного железняка и принял его за модель Земли. Он разметил полюса и принял его южный полюс, притягивавший северный полюс стрелки компаса, за арктическую область Земли, а другой — за антарктическую.

Северный полюс стрелки компаса, помещенной рядом с этим шаром из магнитного железняка, как и ожидалось, показывал «север». Однако в «северном полушарии» этого шара северный конец стрелки компаса, закрепленной соответствующим образом, тоже показывал магнитное погружение, поворачиваясь к телу сферы. Над южным полюсом «арктической области» сферы северный полюс стрелки компаса показывал прямо вниз. В «южном полушарии» сферы южный полюс стрелки компаса указывал вверх, удаляясь от тела сферы, и над «антарктической областью» указывал прямо вверх.

Гильберт решил, что поведение стрелки компаса по отношению к Земле (и ориентация на север — юг, и магнетическое погружение) полностью аналогично ее поведению по отношению к сфере из железняка. Он сделал вывод, что сама по себе Земля является сферическим магнитом с полюсами в Арктике и Антарктиде. Стрелка компаса указывает на север под воздействием той же самой силы, что и притягивает ее к полюсу любого другого магнита. (Именно этот естественный магнетизм Земли выстраивает постепенно области оксида железа и создает магнитный железняк, с которого и началось все изучение магнетизма, бывшее до XIX века.)

Можно легко решить, что магнитные полюса Земли расположены на ее географических полюсах, но это не так. Если бы это было так, стрелка компаса показывала бы более или менее точно на север, а это не так. Во времена Гильберта (1580), например, стрелка компаса в Лондоне показывала на 11° восточнее северного полюса. Угол, на который стрелка отклоняется от истинного Северного полюса, именуется магнитным склонением.  Оно изменяется от места к месту на Земле и в каждом конкретном месте изменяется от года к году.

Сейчас в Лондоне магнитное склонение — 8° к западу от севера, а со времен Гильберта отмечалось склонение даже в 25°к западу от севера. На пути от восточного склонения, имевшего место в XVI веке, к западному склонению, имеющемуся сейчас, одно время склонение было временно нулевым, и тогда стрелка компаса указывала в Лондоне на истинный север. Это было в 1657 году.

Изменения в склонении в зависимости от географического положения были впервые замечены Христофором Колумбом (1451–1506) в его полном открытий путешествии 1492 года. Стрелка компаса, которая показывала явно восточнее севера в Испании, указывала четко на север, когда он достиг середины океана, и четко на запад от севера после того. Он держал это в секрете от экипажа, потому что только этого явного свидетельства нарушения законов природы матросам и не хватало для того, чтобы поднять панику и бунт.

Существование магнитного склонения и его изменения от точки к точке на поверхности Земли можно было бы объяснить тем, что магнитные полюса находятся на некотором расстоянии от полюсов географических. Так оно и есть. Южный полюс Земли как магнита (который притягивает северные полюса стрелок компаса) расположен далеко на севере и потому называется северным магнитным полюсом.  Сейчас он расположен возле арктического побережья Канады, на расстоянии около 1200 миль от географического Северного полюса. Южный магнитный полюс (северный полюс Земли как магнита) расположен на берегах Антарктиды, западнее моря Росса, на расстоянии около 1200 миль от географического Южного полюса.

Эти два магнитных полюса находятся не совсем на противоположных концах Земли, так что соединяющая их линия (магнитная ось) не только составляет угол в 18° с осью географической, но также и не проходит через центр Земли.

 

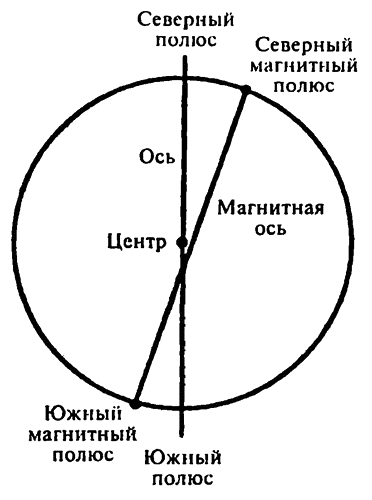
Магнитные полюса Земли

 

Тот факт, что магнитное склонение изменяется со временем, кажется, показывает, что магнитные полюса меняют свое положение, и действительно, положение северного магнитного полюса на несколько градусов сдвинулось с того момента, когда он был впервые найден 100 лет назад.

Несмотря на свой размер, Земля — слабый магнит. Так, даже у небольшого подковообразного магнита магнитная напряженность может достигать 1000 эрстед, а магнитная напряженность поля Земли — только около 3/4 эрстеда даже возле магнитных полюсов, где она является наивысшей. На точках равноудаленных от магнитных полюсов (на магнитном экваторе)  она падает до ¼ эрстеда.

Через точки, на которых наблюдается одно и то же склонение, на Земле можно провести линии. Они называются изогоническими линиями (от греческого слова, означавшего «равные углы»). В идеале их можно считать линиями «магнитной долготы». Однако, в отличие от географической долготы, они не являются участками окружности, а нерегулярно изгибаются в соответствии с местными магнитными свойствами структуры Земли. И конечно же они меняются со временем и их постоянно надо перерисовывать.

Если согласиться с тем, что Земля — это магнит, остается еще определить, почему она магнит. Во второй половине XIX века стало появляться все больше и больше свидетельств из разных источников о том, что ядро Земли на две трети состоит из никеля и железа. Ничего не было проще, чем предположить, что ядро это по какой-то причине намагничено. Однако появлялось также все больше и больше свидетельств, что температура земного ядра достаточно высока, чтобы железо-никелевая масса оставалась жидкой, и явно находится выше точки Кюри. Следовательно, ядро не может быть обычным магнитом, и магнитное поле Земли должно иметь более тонкое происхождение. Я еще вернусь к этому вопросу.

 

 

Магнитное поле

 

Магнитная сила ослабевает пропорционально квадрату расстояния (см. уравнение 9.1), как и гравитационная сила, но между ними есть важные различия. Насколько нам известно, гравитационная сила между двумя телами ни в коей мере не зависит от природы находящейся между ними среды. Другими словами, ваш вес одинаков, не важно, стоите вы прямо на земле, или подставите под ноги лист железа, или деревянную доску, или намыленную резиновую подстилку, или поместите любое другое вещество между собой и землей. Поэтому не изменяется и притяжение Земли Солнцем, когда между ними встает 2000-мильная толща Луны.

Сила же между магнитными полюсами изменяется в зависимости от природы находящейся между ними среды, и уравнение 9.1 точно соблюдается только тогда, когда между полюсами вакуум. Чтобы объяснить это, надо узнать об исследованиях английского ученого Майкла Фарадея (1791–1867).

В 1831 году он заметил нечто, что было замечено на пять веков раньше Петером Перегринусом и, несомненно, еще множеством людей, игравших с магнитами на протяжении веков… Начнем с того, что поместим лист бумаги на магнитную полоску. Если на бумагу насыпать железные опилки и потрясти ее, опилки начнут двигаться и располагаться по линиям, изгибающимся от одного полюса магнита до другого. Каждая линия начинается на одном полюсе и заканчивается на другом, пересекающихся среди них не будет. (Конечно, некоторые линии окажутся незамкнутыми, потому что они выходят за лист бумаги или потому что на больших расстояниях от полюсов их влияние слишком слабо, чтоб заставить железные опилки строго следовать линиям. Все равно можно предположить, что все линии, как бы далеко они ни уходили и какими бы слабыми ни становились, являются непрерывными от полюса к полюсу.)

 

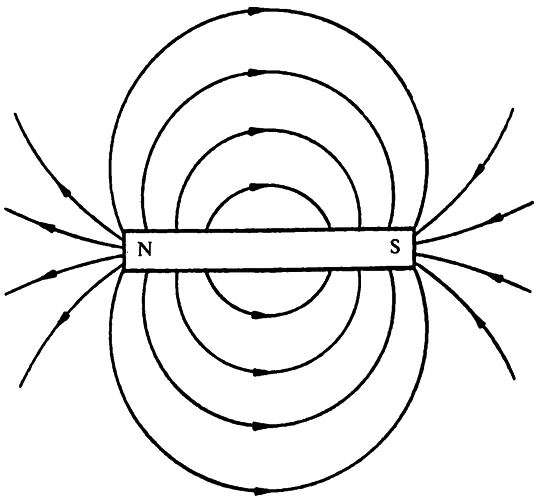
Магнитные силовые линии

 

Форма этих линий зависит от формы магнита и взаимоотношений полюсов. В случае подковообразного магнита линии, собирающиеся около двух полюсов и в пространстве между ними, прямые. То же самое, если северный полюс одного магнитного бруска поднести к южному полюсу другого. С другой стороны, если северный полюс одного бруска поднести к северному полюсу другого, то силовые линии изогнутся наружу в стремлении линий одного магнита избежать линий другого.

Фарадей назвал их силовыми магнитными линиями  и полагал, что они реально существуют. Он считал, что они сделаны из некоего гибкого материала, который растягивается, когда распространяется между двумя различными полюсами, что высвобождает силу, необходимую для его сокращения обратно, как это произошло бы с растянутым резиновым жгутом. И именно это стремление к сокращению и порождает магнитное притяжение, решил Фарадей.

Силовые линии вокруг магнита любой формы или вокруг любой системы магнитов можно визуализировать и без железных опилок. Стрелка компаса всегда располагается так, чтобы лежать вдоль одной из этих линий. Следовательно, выясняя направление стрелки компаса в различных точках пространства, можно выяснить расположение этих линий. Таким образом можно определить и силовые линии Земли как магнита.

Представление Фарадея о материальном присутствии силовых линий просуществовало недолго. К середине XIX века в связи с вопросом о природе света сильные позиции приобрела концепция эфира (см. гл. 6), и силовые магнитные линии стали считать искажением эфира.

С исчезновением в начале XX века концепции эфира нужно было предпринимать дальнейшие шаги. Снова это стало вопросом геометрии самого пространства. Предположим, например, что вы уронили карандаш в цилиндрическое отверстие. Он автоматически сориентируется параллельно оси цилиндра. Если бы цилиндр оказался растянувшейся на многие мили трубой, слегка изгибающейся туда-сюда, упавший карандаш продолжал бы в любой точке ориентироваться параллельно оси трубы, каким бы ни было в данном месте ее направление.

Фактически, если вы не можете увидеть саму трубу, а только карандаш, вы легко можете разметить ее искривления по положениям, которые принимает в различных точках карандаш. То же верно и для стрелки компаса, и для магнитных силовых линий.

Каждый магнитный полюс воздействует на геометрию всего пространства, и эта измененная геометрия (по сравнению с геометрией, какой она была бы в отсутствие магнитного полюса) называется магнитным полем.  Интенсивность этого магнитного поля (насколько его геометрия отличается от обычной немагнитной геометрии пространства) падает пропорционально квадрату расстояния до полюса и вскоре становится слишком маленькой, чтобы ее можно было различить.

Тем не менее магнитное поле каждого существующего магнитного полюса наполняет все пространство, и ситуация становится терпимой только потому, что воздействие любого полюса, находящегося рядом, перевешивает все остальные настолько, что его действие можно считать изолированным (к гравитационным полям это тоже относится).

Представление о магнитном поле устраняет необходимость предполагать, что магнитная сила — это воздействие на расстоянии. Магнит не притягивает железо на расстоянии, а создает поле, которое влияет на кусок железа внутри себя. Поле (представляющее собой геометрию пространства) касается и магнита, и железа, и никакого воздействия на расстоянии предполагать не требуется.

Несмотря на то что магнитные силовые линии не существуют материально, часто бывает удобно нарисовать их в буквальном смысле и использовать для объяснения поведения предметов в магнитном поле. (Делая так, мы используем «модель», то есть представление о Вселенной, не являющееся реальным, но помогающее рассуждать. Ученые используют множество моделей, и они чрезвычайно полезны. Опасность заключается в том, что всегда появляются попытки утверждать реальность моделей, чтобы их можно было использовать за пределами их действия. Может возникнуть и неосознанное сопротивление любым изменениям, которые приносит новое знание, если их нельзя уложить в эту модель.)

Мы можем определить силовые линии между двумя магнитными полюсами в системе СГС (используя сантиметры и дины) таким образом, что одна линия силы будет установлена в 1 максвелл (в честь Максвелла, который так много сделал в связи как с газами, так и со светом). В системе МКС, где те же измерения производятся в метрах и ньютонах, линия силы устанавливается в 1 вебер (в честь немецкого физика Вильгельма Эдуарда Вебера (1804–1891). Вебер — гораздо большая единица, 1 вебер равен 100 000 000 максвеллов. Максвеллы и веберы — единицы измерения магнитного потока, которое можно представить как количество силовых линий, проходящих через данную область, перпендикулярную этим линиям.

Измеряя силу магнитного поля, нужно сосчитать количество силовых линий, проходящих через область определенного размера. Это плотность магнитного потока.

Плотность потока показывает, насколько близко друг к другу проходят силовые линии; чем они более кучны, тем выше плотность потока и тем сильнее магнитное поле в этой точке. В системе СГС единица площади — квадратный сантиметр, так что единица измерения плотности потока — 1 максвелл на квадратный сантиметр. Она получила название 1 гаусс в честь немецкого математика Карла Фридриха Гаусса (1777–1855)[97]. В системе МКС единица измерения площади — квадратный метр, следовательно, единица измерения магнитного потока — 1 вебер на квадратный метр, у этой единицы нет специального названия. Поскольку в квадратном метре 10 000 квадратных сантиметров, а в вебере 100 000 000 максвеллов, то 1 вебер на квадратный сантиметр равен 10 000 гауссов.

Представьте себе магнитный северный полюс и южный полюс, разделенные вакуумом. Силовые линии идут от полюса к полюсу, и плотность потока в любой точке между ними будет иметь определенное значение в зависимости от силы магнита. Если теперь между полюсами поместить какое-либо материальное вещество, даже если сила магнита остается неизменной, плотность потока изменится. Отношение плотности потока в веществе к плотности потока в вакууме называется относительной магнетической проницаемостью. Поскольку это — отношение, то оно выражается просто в цифрах, без единиц измерения.

Проницаемость вакуума принята за 1, и для большинства материальных веществ проницаемость очень близка к 1. Тем не менее уточненные измерения показывают, что точно равной 1 она никогда не является, а бывает иногда чуть больше, а иногда чуть меньше 1. Вещества с проницаемостью чуть большей чем 1 называют парамагнитными, а с проницаемостью меньшей 1 — диамагнитными.

В парамагнитном веществе, проницаемость которого больше 1, плотность потока выше, чем в вакууме. Силовые линии сгущаются в парамагнитном веществе, так сказать предпочитая его окружающему вакууму (или воздуху). Парамагнитное вещество, следовательно, стремится сориентироваться по самой длинной оси параллельно силовым линиям так, чтобы эти силовые линии могли двигаться в избранном веществе по наибольшему расстоянию. И опять же, поскольку плотность потока возрастает по мере приближения к полюсу, имеется тенденция у парамагнитных веществ приближать полюс (то есть притягиваться к нему) таким образом, чтобы сквозь вещество могло проходить как можно больше силовых линий.

С другой стороны, диамагнитные вещества, проницаемость которых меньше 1, имеют плотность потока меньшую, чем вакуум (или воздух). Силовые линии, кажется, избегают его и скапливаются в окружающем вакууме. Следовательно, диамагнитное вещество стремится сориентироваться таким образом, чтобы его наиболее длинная ось была перпендикулярна силовым линиям так, чтобы этим силовым линиям приходилось проходить сквозь вещество минимальное расстояние. Более того, диамагнитные вещества стремятся отодвинуться от полюса (то есть отталкиваются им) в область меньшей плотности потока так, чтобы сквозь него приходилось проходить как можно меньшему количеству линий. Оба эффекта крайне незначительны и становятся заметными только при использовании очень сильных магнитных полей. Первым, кто описал эти эффекты, был Фарадей, обнаруживший в 1845 году, что стекло, сера и резина слегка отталкиваются магнитными полюсами и, следовательно, являются диамагнитными. Наиболее диамагнитным веществом из известных является при обычных температурах элемент висмут. (При чрезвычайно низких температурах, близких к абсолютному нулю, проницаемость некоторых веществ падает до нуля, и диамагнетизм их тогда достигает максимума.)

Парамагнетизм известен сравнительно более широко, и для некоторых веществ проницаемость может быть очень высокой, исчисляясь тысячами. Эти высокопроницаемые вещества и есть те, что мы ранее назвали ферромагнитными. Здесь притяжение магнита и ориентация железных опилок параллельно силовым линиям настолько очевидны, что не заметить их сложно.

Проницаемость (обозначаемая греческой буквой μ  — «мю»), тоже следует учитывать в формуле Кулона (уравнение 9.2), чтобы верно рассчитывать и те случаи, когда полюса разделяет не вакуум:

 

F = mm'/μd2. (Уравнение 9.3)

 

Поскольку μ — знаменатель, то показывается обратное отношение. Диамагнитное вещество с проницаемостью менее 1 увеличивает магнитную силу между полюсами, в то время как парамагнитное вещество силу уменьшает. Последний эффект особенно заметен, когда между полюсами находятся железо или сталь, проницаемость которых исчисляется сотнями или даже тысячами. Брусок железа, касающийся обоих полюсов подковообразного магнита, урезает магнитную силу вне себя настолько, что почти играет роль магнитного изолятора.

 

Глава 10.

ЭЛЕКТРОСТАТИКА

 

Электрический заряд

 

Гильберт, который ввел понятие о Земле как о магните, также изучал силу притяжения натертого янтаря. Он надел на стержень подвижную металлическую стрелку так, чтобы она поворачивалась под давлением совсем незначительной силы. С его помощью Гильберт смог обнаруживать очень слабые силы притяжения и взялся за поиск других веществ, которые, будучи натертыми, обретали бы подобные свойства. Начав свои исследования в 1570 году, он обнаружил, что некоторые драгоценные камни, такие, как алмаз, сапфир, аметист, опал, карбункул, гагат (черный янтарь) и даже обыкновенный горный хрусталь, будучи натертыми, проявляют силу притяжения. Он назвал такие вещества «электриками». Вещества, проявляющие такую силу притяжения, стали называть наэлектризованными  или получившими электрический заряд.

Ряд же других веществ, в частности металлы, оказалось невозможно наэлектризовать, следовательно, они получили характеристику «неэлектриков». В конце концов электричество стали считать чем-то вроде жидкости. Когда вещество, например янтарь, становилось наэлектризованным, считалось, что оно приобрело электрический заряд, остающийся в нем постоянно. Такой заряд был назван статическим электричеством  (от латинского слова, означающего «быть неизменным»), а учение о свойствах электричества в таких условиях получило название электростатика.

Для того чтобы полноценно изучать электрические силы, нужно было собрать достаточное количество этой жидкости — больше, чем могут содержать в себе маленькие кусочки драгоценных и полудрагоценных материалов. Необходимо было найти какое-то дешевое и доступное в больших количествах вещество, подверженное электризации.

В 60-х годах XVII века немецкий физик Отто фон Герике (1602–1686) нашел такой материал — им оказалась сера. Он изготовил из серы сферу размером больше человеческой головы и сделал так, чтобы ее можно было вращать рукояткой. Рука, помещенная на нее, по мере того как сфера поворачивалась под рукой, постепенно наэлектризовывала сферу до беспрецедентной для того времени величины. Герике сконструировал первую механическую электростанцию,  работавшую от трения.

Герике обнаружил много общего между электростатическими и магнитными силами. Например, он выяснил, что имело место электростатическое отталкивание, так же как и электростатическое притяжение, в то время как магнитам тоже были присущи и отталкивание, и притяжение. Опять же вещество, поднесенное к наэлектризованной сере, само временно становилось наэлектризованным, подобно тому как кусочек железа, поднесенный к магниту, сам временно намагничивается. Таким образом, получалось, что наравне с магнитной индукцией существует и электростатическая индукция.

В 1729 году английский исследователь электричества Стефан Грей (1696–1736) наэлектризовал длинные стеклянные трубки и обнаружил, что пробки, помещенные в концы трубок, так же как и шарики из слоновой кости, прикрепленные к этим пробкам длинными палочками, электризуются при натирании стекла. Электрический ток, который образовался во время трения, по-видимому, распространился по веществу через пробку и палки на слоновую кость. Это было первое четкое свидетельство того, что электричеству не обязательно быть полностью статическим, что оно может перемещаться.

В то время как электрический заряд, однажды созданный путем натирания «электрика», распространяется по всему веществу, он не пройдет полностью через него, войдя в одной точке и выйдя в другой. С «неэлектриками» же именно так и происходит — через них ток проходит насквозь. Действительно, через металлы электрический ток проходит чрезвычайно быстро, так быстро, что заряженное вещество теряло свой заряд, становясь разряженным,  если получало контакт с металлом, соприкасающимся, в свою очередь, с землей. Заряд уходил из вещества через металл в огромное тело земли, распространяясь по которому он становился таким слабым, что его уже нельзя было обнаружить.

Это объясняло тот факт, что металлы не электризовались путем натирания. Электрический заряд, как только появлялся, переходил из металла практически в любое тело, соприкасающееся с ним. Грей поместил металлы на блоки канифоли (которые не допускали прохода электрического заряда). В таких условиях куски металла, если их тщательно потереть, действительно наэлектризовывались, так как формировавшийся в металле заряд не мог сразу пройти через канифоль и был, так сказать, пойман в металле. Короче, в конце концов выяснилось, что электрические силы, как и магнитные, присутствуют в материи повсеместно.

По результатам работы Грея вещества были поделены на два класса. Первый класс включает в себя металлы — наилучшие примеры, в частности, золото, серебро, медь и алюминий — материалы, через которые электрический заряд проходит с огромной скоростью. Это электропроводники.  Вещества другой группы, представителями которой являются янтарь, стекло, сера и резина (каучук), — материалы, которые с легкостью электризуются при трении, — оказывают огромное сопротивление электрическому потоку. Это электроизоляторы  (от латинского слова, означающего «остров», так как такой материал может быть использован для изоляции электрических объектов, не давая электричеству покидать их и, таким образом, делая предметы, так сказать, островами электричества).

Представления об электростатическом притяжении и отталкивании развил в 1733 году французский химик Шарль Франсуа Дюфе (1698–1739). Он наэлектризовал маленькие кусочки пробки, прикасаясь к ним уже наэлектризованным стеклянным стержнем, так что электрический заряд частично переходил со стекла на пробку. Несмотря на то что стеклянный стержень притягивал пробку, пока последняя не была заряжена, стержень и пробка отталкивали друг друга, когда пробка заряжалась. Более того, два кусочка пробки, заряженные от стекла, также отталкивали друг друга.

То же самое происходило, когда два кусочка пробки были заряжены прикосновением уже наэлектризованного стержня из канифоли. Однако пробка, наэлектризованная стеклом, притягивала пробку, наэлектризованную резиной.

Тогда Дюфе решил, что существуют два вида электрического заряда, и он назвал их «стеклянным электричеством» и «канифольным электричеством». Здесь, как и в случае с северным и южным магнитными полюсами, аналоги отталкивают друг друга, а противоположности притягиваются.

Против этой теории выступил Бенджамин Франклин. В 1740-х годах он провел эксперименты, которые довольно ясно показали, что заряд «стеклянного электричества» мог нейтрализовать заряд «канифольного электричества», так что не оставалось вообще никакого заряда. Эти два вида электричества не были просто разными, они были противоположными.

В качестве объяснения Франклин предположил, что существует только один электрический заряд и в норме все тела обладают им в определенной степени. Когда этот заряд имеется в нормальном количестве, тело не заряжено и не проявляет электрических свойств. В некоторых случаях в результате трения часть электрического заряда покидала натираемое тело, в других случаях, наоборот, заряд тела возрастал. Когда тело получало избыточный заряд, Франклин предложил считать его положительно заряженным,  а когда заряд уменьшался — отрицательно заряженным.

Положительно заряженное тело притянет отрицательно заряженное, гак как электрический заряд стремится (так сказать) распределиться равномерно, и при контакте электрический заряд перейдет из места, где он в избытке, в место, где он в недостатке. В обоих телах концентрация заряда станет нормальной, и, таким образом, оба тела станут разряженными.

С другой стороны, два положительно заряженных тела будут отталкивать друг друга, так как избыток заряда в одном теле не будет стремиться к прибавлению такого же заряда из другого тела, скорее наоборот. Так же будут отталкиваться и два отрицательно заряженных тела.

Эти понятия помогают объяснить явление электростатической индукции. Если положительно заряженный объект подносится к незаряженному, то избыток заряда в первом будет отталкивать заряд второго и отводить его в дальнюю часть незаряженного тела, делая ближний край второго тела отрицательно заряженным, а дальний край положительно заряженным. (Незаряженное тело останется незаряженным в целом, так как отрицательный заряд одного края будет уравновешивать положительный заряд другого.)

Теперь будет иметь место притяжение между положительно заряженным телом и отрицательно заряженной частью незаряженного тела. Также будет наличествовать и отталкивание между положительно заряженным телом и положительно заряженной частью незаряженного тела. Однако поскольку положительно заряженный край незаряженного тела находится дальше от положительно заряженного тела, чем отрицательно заряженный край, то сила отталкивания будет слабее, чем сила притяжения, и в результате действовать будет сила притяжения.

То же самое происходит, когда к незаряженному телу подносится отрицательно заряженное. В этом случае электрический заряд незаряженного тела приближается к отрицательно заряженному телу. В незаряженном теле формируется положительно заряженная часть, находящаяся около отрицательно заряженного тела (в результате чего имеется сильное притяжение), и отрицательно заряженная часть, находящаяся дальше от отрицательно заряженного тела (в результате чего имеется слабое отталкивание). Общим действием этих двух сил опять же будет притяжение. Таким образом можно объяснить, почему электрически заряженные тела обеих разновидностей одинаково легко притягивают незаряженные тела.

В вопросах притяжения и отталкивания Франклин представлял себе положительный и отрицательный заряды подобно северному и южному полюсам магнита. Однако оставалось одно важное различие. Магнетизм Земли позволял стандартно различать между собой полюса магнита в зависимости от того, на север или на юг указывает определенный полюс. Но способа так же легко отличить отрицательный электрический заряд от положительного не обнаружилось.

По Франклину, положительный заряд получался в результате избытка электричества, но раз уж нет абсолютной разницы в поведении между «стеклянным электричеством» и «канифольным», то как можно определить, какой электрический заряд происходит от избытка заряда, а какой — от недостатка? Обе разновидности различаются только отношением друг к другу.

Франклину пришлось угадывать, четко понимая, что у него один шанс из двух, то есть шансы равны. Он решил, что натертое стекло приобретает электрический заряд и является положительно заряженным, а натертая канифоль теряет электрический заряд и становится отрицательно заряженной. После принятия этого решения все электрические заряды могли быть определены как положительные или отрицательные в зависимости от того, притягивались они или отталкивались зарядом, который уже был определен как положительный или отрицательный.

Со времен Франклина исследователи электричества считают, что поток электричества идет из точки наибольшей положительной концентрации энергии в точку наибольшей отрицательной концентрации, и этот процесс можно считать подобным тому, как поток воды бежит вниз с горы. Всегда существует стремление к ликвидации неравномерности распределения заряда, т. е. к уменьшению заряда в местах избытка и увеличению его в местах нехватки.

С точки зрения Франклина, подразумевалось, что электрический заряд не может ни появляться ниоткуда, ни исчезать в никуда. Если положительный заряд получается из-за притока электрического заряда, этот заряд должен быть получен откуда-то еще, и там, откуда он взялся, должна возникнуть его нехватка. И размер этой нехватки должен быть в точности равен размеру избытка заряда в точке его окончательного местонахождения. Так, если по стеклу терли шелком и оно приобретало положительный заряд, то шелк приобретал равный отрицательный заряд. Суммарный электрический заряд в стекле и шелке был равен нулю перед натиранием и оставался равным нулю после.

Это представление получило достаточно подтверждений со времен Франклина, и мы можем говорить о законе сохранения электрического заряда.

Мы знаем, что электрический заряд не может быть ни создан, ни уничтожен. Суммарный электрический заряд Вселенной постоянен. Нельзя забывать, что мы говорим о суммарном электрическом заряде. Нейтрализация положительного электрического заряда некоторой величины равным по величине отрицательным электрическим зарядом не является уничтожением электрического заряда. Сумма +x  и –x  равна 0; при такой нейтрализации меняется не сам электрический заряд, а лишь его распределение. Это верно и тогда, когда незаряженная система становится такой, что часть ее получает положительный заряд, а другая — равный по величине отрицательный заряд. Ситуация в точности аналогична той, что описывает закон сохранения импульса (см. ч. I).

 

 

Электрон

 

Фактически и в двухзарядной теории Дюфе, и в однозарядной теории Франклина была доля истины. После того как начало приходить понимание внутреннего строения атома в 90-х годах XIX века (эта тема будет подробно рассмотрена в III части нашей книги), было открыто существование субатомарных частиц и то, что одни из них несут электрический заряд, а другие — нет[98].

Из субатомарных частиц, имеющих заряд, самые распространенные — электрон  и протон,  которые противоположно заряжены. Тогда в известном смысле протон и электрон представляют собой два дюфеевских вида зарядов. С другой стороны, протон в условиях электростатических экспериментов проявил себя как абсолютно неподвижная частица, в то время как электрон, самый легкий из них, легко перемещался из одного тела в другое. В этом плане электрон и представляет собой единственный электрический заряд Франклина.

В незаряженном теле число электронов равно числу протонов и заряд отсутствует. Тело наполнено электрическими зарядами обоих видов, но они находятся в равновесии. В результате трения электроны перемещаются. Одно тело приобретает избыток электронов, а в другом получается их нехватка.

Однако обнаружилась одна печальная вещь. Электроны двигаются в направлении, противоположном предположенному Франклином. Франклин не угадал. Там, где, по его мнению, должен был быть избыток электрического заряда, на самом деле была нехватка электронов, и наоборот. По этой причине пришлось считать электрический заряд электрона отрицательным; избыток электронов приведет к отрицательному заряду, чтобы получалась нехватка заряда, по Франклину, в то время как недостаточное количество электронов приведет к положительному заряду, по Франклину. Поскольку электрон получил отрицательное значение заряда, протон получил положительное.

(Инженеры-электрики до сих пор считают, что электрический ток движется от положительного к отрицательному, несмотря на то что физики определили, что электроны движутся от отрицательного к положительному. Для практических целей не имеет значения, каким считать направление тока, ведь направление всегда одно и то же и никаких изменений в процессе тока не происходит.)

Кулон, измерив отношение силы между магнитными полюсами и расстояниями, сделал то же самое для силы между электрически заряженными телами. Здесь стоящая перед ним задача была несколько легче выполнима ввиду важной разницы между магнетизмом и электричеством. Магнитные полюса не существуют сами по себе. Каждое тело, имеющее северный полюс, должно также иметь и южный магнитный полюс. Соответственно на измерение магнитных сил между полюсами влияют и сила притяжения, и сила отталкивания, и это усложняет измерение. Электрические же заряды можно изолировать. Тело может нести только отрицательный или только положительный заряд. По этой причине притяжение может быть измерено без вмешательства усложняющего ситуацию отталкивания, и наоборот.

Кулон обнаружил, что электрическая сила, как и магнитная, изменяется обратно пропорционально квадрату расстояния. В сущности, уравнение, которое он использовал для выражения изменения электрической силы по мере изменения расстояния, было аналогично тому, которое он вывел для магнитных сил (см. уравнение 9.1).

Если электрический заряд двух тел соответственно q  и q’,  а расстояние между ними — d,  тогда F —  сила, действующая между ними (это может быть как сила притяжения, если заряды противоположные, так и сила отталкивания, если заряды одинаковы), может быть выражена так:

 

F = qq’/d2, (Уравнение 10.1)

 

при условии, что между зарядами находится вакуум.

В системе СГС расстояния измеряются в сантиметрах, а силы в динах. Если мы представим, что два равных заряда разделены расстоянием в 1 см и воздействуют друг на друга с силой в 1 дину, то величина электрического заряда —  1 электростатическая единица.

Самый маленький возможный заряд тела — заряд одного электрона[99]. Измерения показали, что он равен –4,8∙10–10 электростатических единиц, где минус означает отрицательный заряд. Это значит, что тело, несущее заряд в 1 электростатическую единицу, содержит около 2 миллиардов лишних электронов.

Другая широко используемая единица заряда в системе МКС — кулон,  названа она в честь физика. Кулон равен 3 миллиардам электростатических единиц. Тело, несущее отрицательный заряд в 1 кулон, содержит примерно 6 миллиардов избыточных электронов, а тело, несущее положительный заряд в 1 кулон, имеет такую же их нехватку.

Представьте себе два электрона на расстоянии 1 см. Так как заряд каждого –4,8∙10–10 электростатических единиц, то общая сила (в данном случае отталкивания) между ними вычисляется с помощью уравнения 10.1, как равная (–4,8∙10–10)2, или 2,25∙10–10 дин.

Два электрона также воздействуют друг на друга гравитационной силой притяжения. Теперь известно, что масса электрона равна 9,1∙10–28 граммов. Сила гравитационного притяжения равна Gmm'/d2,  где G  — гравитационная постоянная, которая равна 6,67∙10–8 дина-см2/г2 (см. ч. I). Гравитационная сила притяжения между электронами равна (9,1∙10–28)2, умноженная на 6,67∙10–8 или 5,5∙10–62 дин. Теперь мы можем сравнить гравитационную и электрическую силы, разделив 2,25∙10–10 на 5,5∙10–62 Частное равно 4∙1042. Это означает, что электрическая сила (или соответствующая магнитная сила в случае магнитов) где-то в 4 миллиона триллионов триллионов триллионов раз больше силы гравитации. Справедливо сказать, что сила гравитации — слабейшая сила, известная в природе.

Тот факт, что гравитация — подавляющая сила в мировом масштабе, происходит полностью из-за того, что мы имеем дело с огромными массами звезд и планет. Хотя все равно, если подумать только о том, что мы, с нашими слабыми мышцами, можем с легкостью поднимать предметы, несмотря на гравитационное притяжение всей Земли, и что то же самое может сделать маленький игрушечный магнит, становится ясно, как гравитационные силы немыслимо малы. И фактически, когда мы имеем дело с телами нормального размера, мы полностью пренебрегаем гравитационными силами между ними.

Электрически заряженные предметы служат источниками энергетических полей,  которые аналогичны магнитным полям. Наравне с магнитными существуют и электрические силовые линии.

Как и магнитные, электрические силовые линии могут проходить сквозь то или иное вещество быстрее или медленнее, чем они прошли бы через равную толщу пустого пространства. Соотношение плотности потока электрических силовых линий, проходящих через среду, к плотности потока, проходящего через пустое пространство, — относительная диэлектрическая проницаемость.  (Этот термин аналогичен относительной проницаемости в случае магнитных полей.)

В общем относительная диэлектрическая проницаемость изоляторов (непроводников) больше чем 1, в некоторых случаях — гораздо больше. Относительная диэлектрическая проницаемость воздуха 1,00054, в то время как резины — около 3, а слюды — около 7. Для воды это 78. Там, где относительная диэлектрическая проницаемость больше 1, электрические силовые линии собираются в веществе и более тесно проходят через него, чем они прошли бы через равный объем пустого пространства. По этой причине непроводники часто называют диэлектриками  (греческий префикс обозначает «через», силовые линии проходят через них). Об относительной диэлектрической проницаемости чаще говорят как о диэлектрической постоянной.

Соответственно формулу Кулона для силы между двумя заряженными частицами можно переписать в более общем виде:

 

F = qq’/κd2, (Уравнение 10.2)

 

где κ диэлектрическая постоянная среды, разделяющей частицы (κ — греческая буква «каппа»).

Электрические силы между заряженными частицами уменьшаются, если между ними помещен диэлектрик; они уменьшаются больше по мере возрастания его диэлектрической постоянной. Составляющие частицы такого вещества, как обычная поваренная соль, например, удерживаются электрическим притяжением. В воде, с ее необычайно высокой диэлектрической постоянной, эти силы соответственно уменьшаются, и, в частности, по этой причине соль быстро растворяется в воде (ее частицы, так сказать, быстро рассыпаются), и вообще вода является хорошим растворителем.

 

 

Электродвижущая сила

 

Если мы потрем стеклянный стержень кусочком шелка, электроны перейдут из стекла в шелк, таким образом, стекло станет положительно заряженным, а шелк — отрицательно. С каждым движущимся электроном положительный заряд стекла и отрицательный заряд шелка будут возрастать, и новым электронам станет все труднее и труднее перемещаться. Для того чтобы выпустить больше отрицательно заряженных электронов из уже положительно заряженного стекла, надо вытягивать электроны наперекор притяжению противоположно заряженного стекла. Чтобы добавить эти электроны к уже заряженному отрицательно шелку, надо перемещать их вопреки отталкиванию одинаково заряженных тел. Так как продолжается увеличение положительного заряда стекла и отрицательного заряда шелка, притяжение и отталкивание становятся все сильнее и сильнее до тех пор, пока простое ручное натирание не потеряет способность перемещать электроны в дальнейшем.

Эта ситуация полностью аналогична той, которая получается при взаимодействии с гравитационными силами у человека, копающего яму. По мере того как он выбрасывает землю на край ямы, уровень земли вокруг вырастает, в то время как уровень земли внутри ямы понижается. Расстояние от дна ямы до верхнего края увеличивается, и становится все труднее и труднее добросить землю наверх. В конце концов копающий не может так высоко добросить землю, чтобы она достигла края, и выкопать яму глубже он не может.

Это указывает на ценность использования знакомых ситуаций, включающих гравитацию как аналогию менее известной ситуации, включающей электрические силы. Давайте же еще немного продолжим рассуждения о гравитационном поле Земли.

Мы можем полагать, что некое тело имеет определенную потенциальную энергию, зависящую от его положения относительно гравитационного поля Земли (см. ч. I). Чем выше тело (т. е. чем больше расстояние от него до центра Земли), тем больше его потенциальная энергия. Чтобы поднять тело против земной гравитации, мы должны увеличить его потенциальную энергию, а для этого должны взять эту энергию откуда-то еще (видимо, из наших мышц).

Количество энергии, которая должна быть добавлена, не зависит от абсолютной величины изначальной потенциальной энергии тела или его конечной энергии, а от разницы потенциальных энергий в двух состояниях. Мы можем назвать эту разницу потенциальных энергий разностью гравитационных потенциалов.

Таким образом, предмет на 80-м этаже небоскреба имеет большую потенциальную энергию, чем предмет, находящийся на 10-м этаже того же самого небоскреба. Все точки на 80-м этаже имеют одну и ту же потенциальную энергию, и все точки 10-го этажа тоже имеют одинаковую потенциальную энергию. Оба этажа представляют собой равнопотенциальные поверхности.

Чтобы сдвинуть предмет с одной точки 10-го этажа на другую (игнорируя силу трения), не понадобится затратить никакой энергии, так как гравитационная разница равна нулю. То же самое будет верно при сдвиге предмета с одного места на другое на 80-м этаже. Несмотря на то что абсолютная потенциальная энергия на 80-м этаже больше, постоянная гравитационная разница также равна нолю.

Таким же образом, не сложнее поднять тело с 80-го этажа на 82-й, чем с 10-го на 12-й. (Если быть совсем точным, на 80-м этаже гравитационная сила чуть слабее, чем на 10-м, но разница столь незначительна, что ею можно пренебречь.) Значение имеет лишь разница в 2 этажа, которая одинакова в обоих случаях. Мы можем измерить разницу в высоте (единственно важную для нас) по количеству энергии, которое мы должны внести, чтобы поднять тело определенной массы на эту разницу в высоте.

В системе МКС единица энергии — джоуль (см. ч. I), а килограмм — единица массы. Таким образом, единица постоянной гравитационной разницы — Дж/кг.

Эта ситуация аналогична наблюдаемой в электрическом поле. Как требуется энергия, чтобы отодвинуть одну массу от другой, точно так же требуется энергия, чтобы отодвинуть положительно заряженное тело от отрицательно заряженного, и наоборот. (Надо затратить энергию, чтобы придвинуть отрицательно заряженное тело к другому отрицательно заряженному телу или положительно заряженное тело к другому положительно заряженному. Для описанной ситуации нет подходящей аналогии в гравитационной системе, так как не существует такого явления, как гравитационное отталкивание.) При отдалении противоположно заряженных тел и приближении одинаково заряженных возрастает электрическая потенциальная энергия; однажды заряженные тела поменяли положение по отношению друг к другу, и разница в их потенциальной электрической энергии — разность электрических потенциалов.

(Понятие об изменении потенциальной энергии гораздо более широко используется в электрофизике, чем в других областях физики, поэтому, когда термин разность потенциалов  используется без определения, он будет с большей вероятностью относиться к разности электрических потенциалов, чем, скажем, гравитационных.)

Опять же, разность электрических потенциалов может быть измерена в количестве единиц энергии, которые нужно приложить к определенному заряду, чтобы переместить его на определенное расстояние.

В системе МКС единица заряда — кулон, следовательно, единица энергетической потенциальной разницы — джоуль на кулон. Эта единица используется так часто, что ей было дано специальное название — вольт — в честь итальянского физика Алессандро Вольты (1745–1827), чья работа будет описана ниже. Из-за этого разность электрических потенциалов (или электрическое напряжение) могут иногда называть «вольтаж». Вернемся опять к гравитационной аналогии и представим предмет, покоящийся на ровной поверхности. Он не имеет стремления к спонтанному перемещению на другой участок этой ровной поверхности, так как разность гравитационных потенциалов между разными точками ровной поверхности равна нулю. С другой стороны, если предмет поднять над поверхностью на расстояние метра и отпустить, то он самопроизвольно упадет, двигаясь из точки с большей потенциальной энергией в точку с меньшей потенциальной энергией. Это спонтанное движение производит разность гравитационных потенциалов.

Таким же образом, и электрический заряд не имеет стремления к спонтанному движению из одной точки электрического поля в другую с таким же уровнем потенциальной энергии. Однако если разность электрических потенциалов имеет место, то у электрического заряда будет тенденция к самопроизвольному движению из точки с большей энергией в точку с меньшей. Поскольку именно разность электрических потенциалов является причиной спонтанного движения энергетического заряда, то мы можем говорить об этой разности как об электродвижущей силе  (силе, которая «двигает электричество»), сокращенно ЭДС. Поэтому часто вместо того, чтобы говорить о потенциальной разнице во столько-то вольт, часто говорят «ЭДС во столько-то вольт».

Чтобы создать разность потенциалов, или ЭДС, сначала надо так или иначе произвести отдаление противоположных зарядов или сближение одинаковых зарядов. Таким образом, с помощью трения стеклянного стержня шелком убирают отрицательно заряженные электроны из стержня (положительный заряд которого возрастает) и добавляют отрицательно заряженные электроны к кусочку шелка (который становится все больше и больше отрицательно заряженным).

Иногда можно создать ЭДС путем сдавливания некоторых кристаллов. Кристалл часто состоит из положительно и отрицательно заряженных частиц, расположенных таким образом, что все положительно заряженные частицы и все отрицательно заряженные частицы сгруппированы около одной центральной точки. Если кристалл сдавить с двух сторон, он подвергнется уплощению и разрушению, и заряженные частицы, составляющие кристалл, будут сдвинуты вместе и будут расплющиваться в стороны. В большинстве случаев оба типа частиц поменяют позицию одинаковым образом и останутся распределены вокруг той же центральной точки.

Однако в некоторых случаях изменения будут такими, что среднее положение отрицательно заряженных частиц немного сместится по отношению к среднему положению положительно заряженных частиц. Это означает, что произведено отделение положительных зарядов от отрицательных, а следовательно, произведена и разность потенциалов между двумя сторонами кристалла.

Этот феномен был открыт Пьером Кюри (который открыл точку Кюри, см. гл. 9) и его братом Жаком в 1880 году. Они назвали феномен пьезоэлектричество  («электричество через давление»).

Ситуация также может быть и обратной. Если кристалл, способный проявлять пьезоэлектричество, поместить в электрическое поле так, чтобы разность потенциалов проходила сквозь кристалл, то он изменит свою форму соответствующим образом. Если потенциальная разница применяется и устраняется много раз подряд, то можно заставить кристалл вибрировать и производить звуковые волны. Если кристалл имеет подходящие размер и форму, то он будет производить звуковые волны такой высокой частоты, что они будут лежать в ультразвуковом диапазоне (см. ч. I). Такого рода взаимные переходы звука и электрического напряжения используются в современных проигрывателях.

 

 

Конденсаторы

 

В работе с электричеством порой бывает необходимо сообщить телу наибольший заряд, затратив при этом как можно меньше усилий. Предположим, у вас есть изолированная металлическая пластина, которая сохраняет любой сообщенный ей заряд. Если вы дотронетесь до такой пластины отрицательно заряженным стержнем, поток электронов хлынет в нее и зарядит пластину отрицательно.

Вы можете продолжать этот процесс до тех пор, пока сохраняется разность потенциалов между стержнем и пластиной, то есть до тех пор, пока вы можете сообщать стержню, натирая его (например, лоскутом шерсти), больший электрический заряд, чем имеется в пластине. Но в конце концов заряд пластины увеличится до такого уровня, что никакие действия уже не придадут стержню заряд больший, чем у пластины. Тогда разность потенциалов станет равной нулю, и заряд уже не будет произвольно перемещаться.

Далее, возьмем вторую металлическую пластину, заряженную положительно, и параллельно расположим ее под первой, но так, чтобы пластины не касались друг друга. Тогда электроны первой пластины под воздействием положительного заряда сгруппируются с той стороны, которая ближе ко второй пластине. (Электроны, скапливаясь с этой стороны, будут находиться ближе друг к другу, «сконденсируются», и такой прибор, состоящий из двух плоских параллельных пластин, расположенных на небольшом расстоянии друг от друга, будет называться конденсатором.)

Другая сторона первой пластины потеряет часть отрицательного заряда, и ее потенциал уменьшится. Таким образом, снова возникнет разность потенциалов между отрицательно заряженным стержнем и этой стороной. Электроны снова перейдут от стержня к пластине, и ее общий заряд станет значительно больше, чем тот, который мог возникнуть в отсутствие второй пластины.

Подобным же образом положительный заряд второй пластины может увеличиться благодаря первой отрицательно заряженной пластине. Так пластины обеспечивают друг другу большую зарядную емкость. (Подобное устройство может также называться конденсатором емкости.)

Чем больше заряд пластин, тем больше разность потенциалов между ними.

Это подобно утверждению: чем выше пик горы и чем ниже долина, тем дольше падать. Между количеством заряда и разностью потенциалов существует такая же прямая зависимость.

Представим, что между пластинами — вакуум, тогда отношение между величиной заряда и разностью потенциалов примет постоянную величину. Выразим это формулой:

 

q/v = c,  (Уравнение 10.3)

 

где q  — заряд в кулонах (Кл); v — разница потенциалов в вольтах (В); c — электрическая емкость,  которая измеряется в кулонах на вольт.

Единица в один кулон на вольт получила название 1 фарад  (в честь Майкла Фарадея)

Таким образом, конденсатор с электрической емкостью в один фарад накапливает заряд, равный одному кулону, на каждой из пластин: на одной — положительный заряд, на другой — отрицательный на один вольт потенциальной разницы между пластинами. Но на самом деле конденсаторы с такой большой электрической емкостью обычно не встречаются. Как правило, за единицу измерения принимают микрофарад  (одна миллионная фарада) или микромикрофарад  (одна миллионная миллионной фарада).

Теперь предположим, что между пластинами поместили диэлектрик (непроводник). Диэлектрик уменьшает силу притяжения между противоположными зарядами и, таким образом, сокращает количество работы, которая необходима для разделения этих зарядов. Но, как объяснялось выше, разность потенциалов есть количество работы, затраченной на разделение противоположных зарядов. Это значит, что разность потенциалов между пластинами конденсатора при наличии диэлектрика равняется отношению v/κ,  где κ  — диэлектрическая постоянная.

Если мы обозначим электрическую емкость конденсатора с диэлектриком как c', то тогда получим следующее:

 

c' = q/(v/κ) = κq/v = κ(q/v). (Уравнение 10.4)

 

А сопоставив уравнения 10.3 и 10.4, получим

 

c' = κc.  (Уравнение 10.5)

 

Очевидно, что наличие диэлектрика между пластинами увеличивает электрическую емкость конденсатора прямо пропорционально его диэлектрической постоянной. Диэлектрическая постоянная воздуха равняется всего лишь 1,0006 (а за 1 принимается проницаемость вакуума), поэтому воздух между пластинами можно считать средой, равнозначной вакууму. Диэлектрическая постоянная стекла равна примерно 5, следовательно, электрическая емкость пластин, разделенных стеклом, увеличивается в пять раз. Соответственно, конденсатор, разделенный стеклом, накопит заряда в пять раз больше, чем тот, который имеет в качестве диэлектрика воздух.

Электрическую емкость можно увеличивать посредством уменьшения расстояния между пластинами, или посредством увеличения площади поверхности пластин, или применяя тот и другой способ одновременно. Если расстояние между пластинами сокращается, то уменьшается разность потенциалов (так же как и разность гравитационных потенциалов уменьшается, если объекты разделяют не два этажа, а один). Если это так, то v из уравнения 10.3 уменьшается, в то время как q  остается неизменным, а с  непременно возрастает. Опять же при увеличении площади поверхности пластин появляется больше места для скопления зарядов. Следовательно, q  увеличивается в уравнении 10.3, а значит, и с  тоже.

Конденсатор с большими пластинами может быть громоздким, но такого же результата можно добиться, объединив несколько конденсаторов между собой, соединив положительно заряженные пластины друг с другом при помощи проводникового материала, например металлического стержня, и так же поступив с отрицательно заряженными. Таким образом, любой заряд, добавленный к одной из пластин, распределится по всем пластинам того же типа, и множество маленьких пар пластин приобретут свойства одной большой пары. Таким образом сгруппированные конденсаторы называют последовательно соединенными.

В такой группе конденсаторов один набор пластин может быть неподвижным, а другой — поворотным. Вращая рукоятку, соединенную со стержнем, на который насаживаются пластины, можно передвигать отрицательно заряженные пластины вдоль линии положительно заряженных, и только те группы пластин, которые находятся прямо напротив друг друга, будут наиболее активными частями конденсатора. Следовательно, когда подвижная часть конденсатора двигается вдоль линии, электрическая емкость постоянно возрастает, если же она смещается, электрическая емкость уменьшается. Такой конденсатор называется регулируемым конденсатором.

Наэлектризованное тело можно разрядить, дотронувшись до него пальцем, если человек, касающийся этого предмета, стоит на поверхности без изоляции, особенно на земле, то есть если человек заземлен.  Если предмет отрицательно заряжен, то поток электронов, устремившись из него, будет проходить через человека в землю, пока отрицательный заряд не рассеется. Если предмет положительно заряжен, то поток электронов, наоборот, устремится из земли через человека в этот предмет, пока положительный заряд не будет нейтрализован. В любом случае поток электронов проходит через тело человека.

Поскольку ощущения живого организма передаются посредством потока слабейших зарядов, движущихся по нервам, неудивительно, что можно ощутить поток электронов, появляющийся в результате разряжения заряженного предмета. Слабый заряд воспринимается как покалывание. Сильный — как внезапный тяжелый удар, который причиняет резкую боль. Такое явление называют электрическим шоком.  (Подобно физическому удару, поток электронов тоже может убить.) Так как конденсаторы накапливают большое количество электрических зарядов, то шок, полученный от них, гораздо сильнее того, который можно получить от обычного наэлектризованного стержня тех же размеров.

Это неприятное свойство конденсаторов было обнаружено случайно в 1745 году, когда они только начали появляться. Самый первый конденсатор представлял собой стеклянный сосуд, покрытый изнутри и снаружи металлической фольгой. Сосуд закупоривали, а пробку протыкали металлическим стержнем. Металлическая цепь, подвешенная к стержню, касалась фольги внутри сосуда.

Предположим, что фольга снаружи сосуда заземлена. Если коснуться металлического стержня, торчащего из пробки, отрицательно заряженным стержнем, то электроны, пройдя через него, распределятся на внутреннем покрытии из фольги. Электроны на внутреннем покрытии оттолкнут электроны на внешнем покрытии и отправят их в землю. Если повторить это несколько раз, то на внутреннем покрытии накопится большой отрицательный заряд, а на внешнем — большой положительный. Благодаря тому что листы фольги оказались конденсатором, разделенным стеклом, величина получившегося заряда превзошла все ожидания первых экспериментаторов.

Первые ученые, которые создали конденсаторы подобного типа, — немецкий экспериментатор Эвальд Юрген фон Клейст в 1745 году и голландский физик Питер ван Мушенбрук (1692–1761) в 1746 году — испытали удивление и даже ужас, когда разрядили устройство и подверглись электрическому шоку. Фон Клейст сразу же прекратил всякие эксперименты, а ван Мушенбрук продолжил исследования, но с крайней осторожностью. Поскольку ван Мушенбрук работал в университете Лейден в Нидерландах, его конденсатор называется лейденской банкой.

Во второй половине XVIII века лейденская банка использовалась в различных важных экспериментах, связанных с электричеством. Можно было собрать и высвободить заряд столь огромной величины, что он мог вызвать шок у сотни взявшихся за руки людей, убивать маленьких животных и т. д. Сами по себе эти эксперименты не представляли особой важности, но они были необходимы для демонстрации электрического феномена и для привлечения внимания научных кругов (и широкой общественности тоже).

 

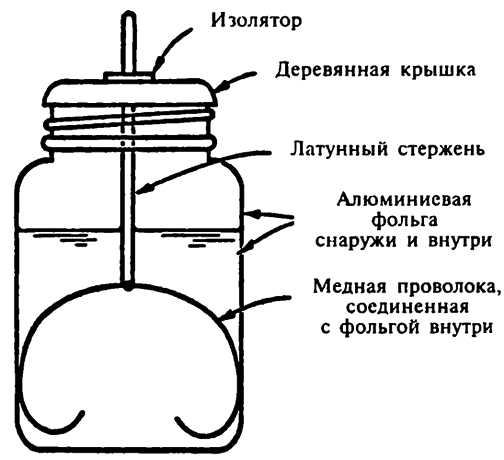
Лейденская банка

 

В частности, лейденская банка демонстрировала вопрос, связанный с разряжением через воздух. Сухой воздух является изолятором, но никакая изоляция не совершенна, и, если заряд какого-то предмета достаточно велик, он сможет пройти сквозь заданный изолятор. (Представьте груз, покоящийся на деревянной доске, которая подвешена в нескольких футах от земли. Доска в данном случае является своего рода изолятором в том смысле, что она не позволяет грузу упасть, несмотря на разность гравитационных потенциалов между землей и грузом. Если массу груза постоянно увеличивать, то настанет момент, когда доска сломается и груз упадет на землю. В терминах электрофизики, «изолятор» будет пробит, а груз «разряжен».)

Когда электрический заряд проходит через обычно являющуюся изоляционной прокладку из воздуха, под воздействием электрической энергии воздух нагревается до такой степени, что начинает светиться. Разряд сопровождается искрой. Горячий воздух увеличивается в объеме, а затем, отдавая свое тепло в окружающую атмосферу, снова сжимается. Этот процесс вызывает вибрации звуковых волн, поэтому разряд сопровождается не только сверканием, но еще и треском. Такие явления были замечены даже Герике в его опыте с заряженным шариком из серы. Лейденская банка с ее огромным накопленным зарядом производит больший эффект в создании искр и треска.

Франклин, который много работал с лейденской банкой, не мог не заметить сходства между разряжением и такими природными явлениями, как гром и молния. Лейденская банка порождает миниатюрные вспышки молнии и раскаты грома. И наоборот, земля и небо — это гигантские пластины лейденской банки. Франклин пытался доказать, что это больше чем просто поэтический образ.

В июне 1752 года он запустил воздушного змея во время грозы. Он привязал заостренный металлический стержень к деревянному каркасу змея и прикрепил к нему кусок шнура. Все это он соединил с веревкой, на которой держится змей. Еще он привязал металлический ключ к веревке. Во избежание электрического удара Франклин спрятался под навес и держал веревку со змеем при помощи изолирующего шелкового шнурка.

Змей исчез в облаках, и Франклин заметил, что волокна веревки торчат в разные стороны, отклоняясь друг от друга, как будто они получили электрический заряд и отталкивали друг друга. По-видимому, ключ тоже получил заряд. Франклин осторожно приблизил костяшки пальцев к ключу, появилась искра — точно такая же искра, сопровождаемая точно таким же треском, которые ожидают от лейденской банки. Затем Франклин достал лейденскую банку, которую принес с собой, и зарядил ее небесным электричеством. Результат получился абсолютно таким же, как от заряда электрической фрикционной машиной. Таким образом, он доказал, что и в небесах существует электричество и что молния — это гигантский электрический разряд, а гром — это мощный треск, сопровождающий такой разряд.

Он не остановился на этом. Франклин исследовал различные способы разряжения. В своих опытах он использовал предметы разной формы. Так, если поднести к предмету металлическую сферу, предмет разрядится через воздух на расстоянии в один дюйм. Если к тому же телу с тем же самым размером заряда поднести металлическую спицу, разряд возникнет на расстоянии в 6–8 дюймов. Вывод можно было сделать такой: заряженное тело легче разрядить острым предметом, чем тупым. Кроме того, при разряжении тела острой спицей искры и треск не наблюдались. (Тем не менее сам факт разряжения тела определялся очень просто: заряженное тело внезапно перестало отталкивать подвешенный вблизи пробковый шарик с таким же зарядом.)

Франклин догадался, что такое явление может быть полезным для решения проблемы, связанной с грозой. Если на крышу здания поместить высокий заостренный металлический стержень, то он сможет довольно эффективно разряжать заряженные облака, прежде чем они заполнят вспышкой молнии пробел между собой и крышей. А если присоединить к такому громоотводу  проводники, разряд будет отводиться в землю, не причиняя вреда зданию. Таким образом дома можно защищать от грозы.

И действительно, это приспособление работало очень хорошо. В следующие 20 лет здания всей Европы и Америки находились под защитным покровом изобретения Франклина. Франклин стал первым великим ученым Нового Света, и благодаря этому открытию о нем узнали в Европе (факт, который имел важные политические последствия в дальнейшем, когда Франклин отправился во Францию во время американской революции, четверть века спустя после легендарного запуска змея). С изобретением громоотвода изучение электростатики достигло апогея. К концу XVIII века появился новый аспект в изучении электричества, и электростатика отошла на задний план.

 

Глава 11.

ЭЛЕКТРИЧЕСКИЕ ТОКИ