В 80-х годах XIX века Михельсону (тому самому, который позже измерил скорость света) пришло в голову, что можно придумать способ измерения абсолютного движения.
Точка зрения того времени гласила, что свет состоит из эфирных волн, и, если бы эфир двигался, он мог бы нести собственные вибрации (свет) с собой. Если бы эфир двигался по направлению от нас, он уносил бы от нас свет и, следовательно, задерживал бы свет, иначе говоря, уменьшал бы скорость света. Если бы эфир двигался от нас со скоростью в два раза меньшей скорости света, свет потерял бы половину своей скорости по отношению к нам и соответственно в два раза дольше добирался бы к нам из некоей фиксированной точки. Таким же образом, если бы эфир двигался по направлению к нам, он бы достигал нас быстрее.
Точнее, физики считали, что эфир сам по себе не двигается ни при каких обстоятельствах. Однако Земля должна, казалось, неизбежно двигаться по отношению к эфиру. В том случае, если принять Землю как неподвижную, эфир будет казаться движущимся по отношению к нам, поскольку мы закреплены на Земле. Тогда проявлялось бы то, что получило название «эфирный ветер».
Если бы эфирного ветра не существовало, если бы Земля находилась в абсолютном покое, тогда свет двигался бы во все стороны с одной и той же скоростью. Кажется, что так оно и есть, но, скорее всего, это так только потому, что скорость эфирного ветра слишком мала по сравнению со скоростью света; следовательно, свет очень незначительно меняет свою скорость с переменой направления. Учитывая, что точное измерение скорости света представляло собой на тот момент очень сложную задачу, неудивительно, что небольшая разница в скорости оставалась незамеченной.
Однако в 1881 году Михельсон изобрел устройство, достаточно тонкое, чтобы произвести эту работу.
В этом приборе свет с определенной длиной волны падал на стеклянную плоскость под углом 45°. Задняя поверхность стекла была «полупосеребренной», то есть поверхность была покрыта достаточным слоем серебра, чтобы отражать половину света, а другую половину пропускать. Пропущенный свет продолжал движение в том же направлении, а отраженный двигался под прямым углом к этому направлению. Оба световых луча отражались зеркалом и возвращались обратно на полупосеребренную стеклянную плоскость. Часть изначально отраженного пучка лучей теперь проходила насквозь, а часть изначально пропускаемого пучка теперь отражалась. Таким образом, оба луча воссоединялись[91]. В результате единый луч света разбивался надвое; две половинки отсылались в направлениях перпендикулярных друг другу, возвращались и вновь соединялись в один луч.
Соединяясь, два луча производили линии интерференции, как это происходило с двумя лучами из эксперимента Янга. Одно из зеркал могло быть так настроено, что расстояние, пройденное лучом до этого зеркала и обратно, могло изменяться. Когда зеркало настроено, линии интерференции двигаются. По количеству линий, проходящих перед взглядом, когда зеркало перемещается на определенное расстояние, можно определить длину волны света. Чем большее количество зубцов проходит перед взглядом, тем короче длина волны.
Михельсон определял длину волны света своим инструментом, который он называл интерферометром («измерителем по интерференции»), настолько точно, что он предположил, что длина волны некоторых определенных спектральных линий может служить фундаментальной единицей изменения длины. В то время за такую фундаментальную единицу измерения был только что принят международный эталон метра. Это было расстояние между двумя тонкими отметками на брусе из платино-во-индиевого сплава, хранимого в Севре, пригороде Парижа.
В 1960 году предложение Михельсона было в конце концов одобрено и эа фундаментальную единицу измерения длины было принято явление природы, а не рукотворный предмет. Оранжево-красная спектральная линия разновидности редкого газа криптона была принята за стандарт. Сейчас метр официально установлен как величина в 1 650 763,73 раза больше волны этого света.
Но Михельсон желал большего, чем установление длины волны спектральных линий. Он признавал тот факт, что пучок света в интерферометре был расщеплен на две половины, которые двигались под прямым углом друг к другу. Предположим, что один из этих двух лучей идет по эфирному ветру. Тогда его скорость будет равной с (скорость света по отношению к эфиру) плюс v (скорость источника света по отношению к эфиру).
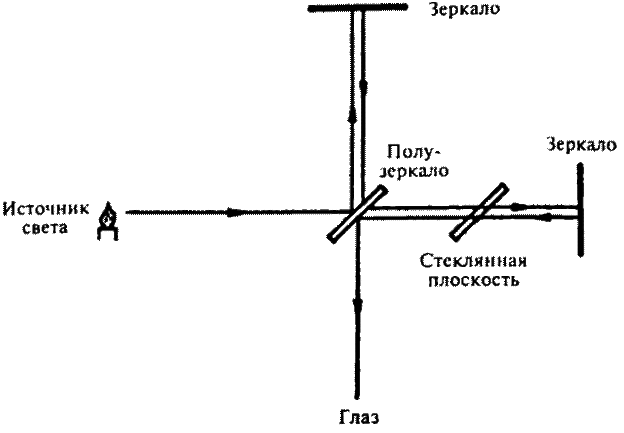
Интерферометр
Если расстояние от отражающего зеркала до полупосеребренной призмы принять за d, то время, которое понадобится свету, чтобы преодолеть расстояние от полупосеребренной призмы до отражающего зеркала, будет равным d/(c + v). После отражения свет вновь преодолеет расстояние d точно в обратном направлении. Теперь он будет двигаться против эфирного ветра и будет замедлен, его полная скорость будет равна с – v, а время, требующееся ему для того, чтобы вернуться, будет d/(c – v). В результате время, которое потребуется лучу на то, чтобы пройти туда и обратно, будет вычисляться по формуле:
t1 = d/(c + v) + d/(c – v) = 2dc/(c2 - v2). (Уравнение 6.1)
Однако в то же время вторая половина луча движется под прямым углом к первой; возвращается она также под прямым углом к первой. Она не движется ни по эфирному ветру, ни против него. И туда и обратно этот второй луч движется «поперек ветра».
Время, которое потребуется лучу света на то, чтобы преодолеть путь туда и обратно (t2), может быть высчитано с помощью плоскостной геометрии[92] и оказывается равным:

Поделив уравнение 6.1 на уравнение 6.2, мы найдем отношение времени, которое требуется на преодоление расстояния по эфирному ветру и против него, ко времени, которое требуется на преодоление того же расстояния поперек эфирного ветра. Мы получим:
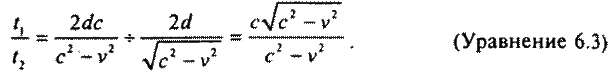
Выражение в самой правой части уравнения 6.3 принадлежит известной формуле (а√х)/х, и если и числитель и знаменатель разделить на √х , то получим эквивалентное выражение a/√х. Соответственно уравнение 6.3 можно упростить до:

Дальнейшее упрощение возможно в случае умножения и числителя и знаменателя на √(1/с2) (умножение числителя и знаменателя на одно и то же число, естественно, не меняет значения всего выражения). Тогда числитель уравнения 6.4 становится равным c√(l/c2) = c/c = 1. Знаменатель же становится равным √(c2/c2 – v2/c2. Соответственно уравнение 6.4 может быть записано в виде:
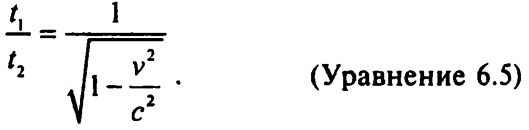
Если источник света неподвижен по отношению к эфиру, то v = 0 и t1/t2 = 1. В таком случае время, затраченное лучом света, движущимся по эфирному ветру и против него, будет таким же, как и время, затраченное лучом света, движущимся поперек эфирного ветра. (На самом деле это время одно и то же для лучей света, движущихся во всех направлениях,) Если движущееся зеркало настроено таким образом, чтобы два луча света проходили в точности одно и то же расстояние, вернутся они точно одновременно, и линий интерференции не возникнет. Более того, не будет возникать линий интерференции и при повороте прибора таким образом, чтобы лучи света двигались в других направлениях.
Однако, если по отношению к эфиру свет движется, то v больше чем 0, следовательно, 1 – v2/c2 меньше единицы и t1/t2 больше единицы. Свет, движущийся по эфирному ветру и против него, будет дольше преодолевать определенное расстояние, чем свет, движущийся поперек него. На самом деле это отношение не намного больше единицы для любой разумной скорости по отношению к эфиру. Даже если источник света движется со скоростью 0,1 скорости света (так, что v равно огромной цифре в 30 000 км/с), это отношение будет составлять всего 1,005. Для обычных же скоростей это отношение будет совсем мало.
Тем не менее разница во времени была бы достаточной, чтобы разделить два луча света и привести к появлению линий интерференции. Естественно, невозможно было заранее знать направление эфирного ветра, но это не имело значения. Прибор можно было повернуть в любом направлении, и передвижное зеркало могло быть настроено таким образом, чтобы устранять линии интерференции. Если прибор повернуть теперь, то лучи света поменяли бы направление и теперь испытывали бы другое воздействие со стороны эфирного ветра, так что линии интерференции появились бы вновь.
По расстоянию между линиями можно было определить скорость источника света по отношению к эфиру. Поскольку источник света был жестко закреплен на Земле, это означало определить скорость Земли по отношению к эфиру, то есть установить абсолютное движение Земли. Если бы это было сделано, то можно было бы установить абсолютное движение всех тел, зная их движение по отношению к Земле.
С помощью американского химика Эдварда Уильямса Морли (1838–1923) Михельсон в 1886 году провел свой эксперимент. Он проводил его и до того, один, но ни разу не делал этого в условиях, которые бы его удовлетворяли. Теперь же он и Морли доскональнейшим образом закрепили интерферометр и применили фантастические предосторожности против возможных ошибок.
Снова и снова они повторяли свой эксперимент, и результаты оказывались одними и теми же — негативными! Когда они настраивали прибор, чтобы удалить линии интерференции, они не расширялись сколько-нибудь заметным образом при любых поворотах интерферометра. Можно было подумать, что им не повезло и для проведения эксперимента они выбрали момент, когда Земля не двигалась относительно эфира. Однако Земля движется по эллиптической орбите вокруг Солнца и ежемоментно меняет направление своего движения. Если в один день она оказалась неподвижной относительно эфира, то в следующий день она должна была двигаться.
Михельсон и Морли провели тысячи наблюдений в течение многих месяцев и наконец в июле 1887 года объявили свое заключение. Никакого эфирного ветра не было!
Я углубился в детали этого эксперимента из-за его шокирующего результата. Заявить об отсутствии эфира означало заявить о том, что, скорее всего, не существует способа установить абсолютное движение. А если это так, что станет с законами Ньютона и со всей картиной Вселенной, основанной на этих законах?
Физикам принесло бы облегчение извещение о том, что в эксперименте Михельсона — Морли были погрешности и эфирный ветер, несмотря ни на что, существует. Однако этот эксперимент повторялся снова и снова с 1887 года. В 1960 году для этой цели были использованы гораздо более точные приборы, чем интерферометр, но результат оставался прежним. Эфирного ветра не существует. Этот факт оставалось просто принять и изменить соответствующим образом картину Вселенной.
Сокращение Фитцджеральда
Естественно, предпринимались попытки объяснить результаты эксперимента Михельсона — Морли в рамках теории эфира. Наиболее успешная попытка принадлежала ирландскому физику Джорджу Франсису Фитцджеральду (1851–1901), который в 1893 году предположил, что все предметы укорачиваются в направлении своего абсолютного движения, так сказать сплющиваясь под воздействием эфирного ветра. Размер такого «укорачивания» будет возрастать вместе со скоростью абсолютного движения, поскольку давление эфирного ветра тоже будет возрастать.
Фитцджеральд предположил, что для любой заданной скорости длина (l) предмета или расстояния между предметами будет фиксированным образом относиться к длине L0 того же самого предмета или расстояния в состоянии покоя; L0 можно назвать длиной покоя. Это отношение выражается формулой √(l 2 – v 2/с2), где c — скорость света в вакууме, v — скорость тела, и то и другое — по отношению к эфиру. Другими словами,

Коэффициент Фитцджеральда равен знаменателю выражения из уравнения 6.5, которое представляет отношение расстояний, проходимых двумя лучами в интерферометре. Будучи умноженным на коэффициент Фитцджеральда, значение уравнения 6.5 становится равным 1.
Расстояние, проходимое лучом света, движущимся по эфирному ветру и против него, теперь уменьшается ровно на такую длину, которую луч проходит за то же время, за которое и луч, движущийся поперек эфирного ветра. Другими словами, существование эфирного ветра заставит один луч тратить большее время, но существование сокращения Фитцджеральда, источником которого является тот же самый эфир, позволяет лучу совершить свой путь за то же самое время, которое требовалось бы ему, если бы никакого эфирного ветра не существовало.
Эти два эффекта эфирного ветра взаимно аннулируют друг друга, и это напомнило физикам отрывок из стихотворения Льюиса Кэрролла, герой которого собирался покрасить усы в зеленый цвет и прикрыть их большим веером, чтобы никто этого не увидел.
Книга Кэрролла была написана в 1872 году, поэтому вряд ли он имел в виду сокращение Фитцджеральда, но описано оно здесь один к одному.
На обычных скоростях это сокращение чрезвычайно мало. Земля движется по своей орбите вокруг Солнца со скоростью 30 километров в секунду (по отношению к Солнцу), что по земным стандартам является немалой скоростью. Если v принять равным 30 и подставить это значение в уравнение Фитцджеральда, мы получим √(1 - 302/3000002), что равняется 0,999995. В таком случае сокращенный диаметр Земли будет равен 0,999995 от ее диаметра, перпендикулярного этому направлению (если, конечно, принять Землю за идеальную сферу). Величина этого сокращения составит 62,5 метра.
Если измерить диаметр Земли по всем направлениям и установить то направление, в котором ее диаметр сокращен, можно будет установить направление движения Земли по отношению к эфиру. Более того, исходя из величины этого сокращения можно вычислить абсолютную скорость Земли по отношению к эфиру.
Но есть затруднение. Оно заключается не в малой величине сокращения, поскольку не важно, насколько оно мало, если его можно обнаружить в принципе. Дело в том, что его нельзя обнаружить, находясь на Земле. Когда мы находимся на Земле, все инструменты, которые мы могли бы использовать для измерения диаметра Земли, находятся в том же движении, что и Земля, и подвергаются тому же сокращению. Сокращенный диаметр измерялся бы сокращенными инструментами, и сокращение не было бы обнаружено.
У нас могло бы что-нибудь получиться, если бы мы сошли с Земли и, не разделяя ее движения, измерили бы ее диаметр по всем направлениям (очень точно), пока она пролетала мимо. Это не очень реально, но только так это было бы выполнимо.
Чтобы сделать это на практике, надо найти что-то, что двигалось бы очень быстро, и при этом чтобы мы не разделяли этого движения. В качестве таких объектов подошли бы субатомные частицы[93], имеющие скорость относительно поверхности Земли от 10 000 км/с до скоростей, близких к световым.
Сокращение Фитцджеральда на таких скоростях становится очень значительным. Например, скорость может быть достаточно высокой, чтобы длина движущегося тела сократилась вдвое. В этом случае √(12 – v2/с2) = ½, и если мы решим это уравнение для v, то получим его равным √(3с2/4). Поскольку с = 300 000 км/с, то √(3с2/4) = 260 000 км/с. На этой огромной скорости, в 7/8 света, предмет сокращается до половины своей длины, а некоторые субатомные частицы движутся еще быстрее.
На еще более высоких скоростях сокращение становится еще более заметным. Предположим, что скорость тела становится равной скорости света. При таких условиях v равно с, и коэффициент Фитцджеральда принимает значение √(12– c2/c2), что равняется 0. Это означает, что по уравнению 6.6 длина движущегося тела (L) становится равной его длине покоя (L0), умноженной на нуль. Другими словами, на скорости света все тела вне зависимости от их длины покоя сокращаются совершенно и становятся бесконечно тонкими блинами.
Но что, если скорость света будет превышена? В этом случае v становится больше, чем c, выражение v2/c2 становится больше 1 и выражение 1 — v2/c2 становится отрицательным числом. Пропорция Фитцджеральда становится квадратным корнем из отрицательного числа, а это то, что математики именуют «мнимым числом». Длина, представляемая мнимым числом, безусловно, имеет математическую ценность, но работать с такой физической величиной невозможно.
Это было первым знаком того, что скорость света должна иметь какое-то важное значение для Вселенной — как наивысшая, в каком-то смысле, скорость. На самом деле никогда не наблюдалось, чтобы субатомные частицы двигались со скоростью выше, чем скорость света, в вакууме, хотя и наблюдались скорости выше чем 0,99 скорости света. На таких скоростях субатомные частицы должны были бы истончиться в направлении своего движения, но, увы, они так малы, что невозможно на практике измерить их длину, когда они пролетают мимо, и нельзя сказать, сокращены они или нет. Однако, если для проверки наличия пропорции Фитцджеральда нельзя использовать субатомные частицы, можно подойти по-другому…
Сокращение Фитцджеральда дополнил, придав ему правильную математическую форму, голландский физик Хендрик Антон Лоренц (1853–1928), поэтому это явление иногда называют «сокращение Лоренца — Фитцджеральда».
Лоренц продолжил доказательство того, что, если применять сокращение Фитцджеральда к субатомным частицам, несущим электрический заряд, можно сделать вывод, что масса тела должна возрастать в той же пропорции, в которой сокращается его длина. Короче, если его масса в движении равна m, а масса покоя — m 0, то
m = m0/√(1 - v2/c2). (Уравнение 6.7)
И опять же, прибавление массы на обычных скоростях очень мало. На скорости в 260 000 км/с масса движущегося тела увеличивается в два раза, а на более высоких скоростях — еще больше. Когда скорость движущегося тела становится равной скорости света, v = c, то уравнение 6.7 приобретает вид: m = m0/0. Это означает, что масса движущегося тела становится больше любой доступной величины. (Обычно говорят, что масса движущегося тела становится бесконечной.) И опять же скорости больше световой должны приводить к появлению масс, выражаемых мнимыми числами, для которых не предвидится физических интерпретаций. Снова подчеркивается ключевая важность скорости света в вакууме.
Но очень быстро движущиеся субатомные частицы, развивающие скорости вплоть до 0,99 скорости света, должны значительно увеличивать свою массу; и если длина субатомных частиц не может быть измерена по мере их пролетания мимо, их массу легко можно измерить.
Масса таких частиц может быть получена путем измерения их инерции, то есть силы, необходимой для придания им ускорения. На самом деле именно количество инерции Ньютон использовал для определения массы в своем втором законе (см. ч. I).
Полет заряженных частиц можно искривить в магнитном поле. Таким образом, магнитное поле придает частицам ускорение, и радиус искривления их полета и есть показатель величины инерции частицы, следовательно, и ее массы.
Из искривления пути частицы, движущейся на малой скорости, можно высчитать массу частицы и затем предсказать, как ее путь должен искривиться, проходя через то же самое магнитное поле на более высоких скоростях при условии, что его масса окажется прежней. Действительные же измерения искривления пути частиц, движущихся на высоких скоростях, показали, что эти искривления были менее значительными, чем ожидалось. Это можно объяснить увеличением массы при увеличении скорости, и, когда это было сделано, получившиеся данные четко укладывались в уравнение Лоренца.
Веер выпал, и зеленые усы оказались у всех на виду. Уравнение Лоренца совпало с наблюдаемыми фактами. Поскольку оно было основано на уравнении Фитцджеральда, то явление сокращения тоже оказалось совпадающим с фактами, и это объяснило негативные результаты эксперимента Михельсона — Морли.
Глава 7.
ОТНОСИТЕЛЬНОСТЬ
Специальная теория
Если приращение массы движущейся с большой скоростью заряженной частицы является результатом ее движения относительно эфира, то напрашивается новый способ измерения такого движения. Предположим, что одни заряженные частицы взвешивают по мере того, как они пролетают в одном направлении, другие — пока они пролетают в другом направлении, и т. д. Если охватить все направления, то получится, что одни частицы должны будут двигаться по эфирному ветру, в то время как другие, движущиеся в противоположном направлении, будут перемещаться против него.
Те частицы, что предположительно движутся против эфирного ветра, будут двигаться быстрее по отношению к эфиру и прибавят больше массы, чем те, которые будут двигаться с той же скоростью (относительно нас) по эфирному ветру. По изменению прибавления массы в зависимости от перемены направления можно установить скорость эфирного ветра, а стало быть, и абсолютное движение Земли.
Однако и этот способ оказался неудачным, так же как и эксперимент Михельсона — Морли. Прибавление массы по мере движения оказалось одним и тем же независимо от направления движения. Более того, все эксперименты, целью которых было установить абсолютное движение, провалились.
В общем-то еще в 1905 году молодой швейцарский физик — немец по месту рождения — Альберт Эйнштейн (1879–1955) уже понял, что поиск способов измерения абсолютного движения ни к чему не приведет. Допустим, что мы возьмем быка за рога и примем за данное, что невозможно измерить абсолютное движение каким бы то ни было допустимым методом[94], и рассчитаем следствия из такого решения. Итак, первое допущение Эйнштейна было таково: любое движение должно быть признанным по отношению к некоему объекту или некоей системе объектов, произвольно принятых за находящиеся в покое; любой объект или система объектов (любая система отсчета) могут быть приняты с равной верностью за находящиеся в покое. Другими словами, нет ни одного объекта, который находится в «более реальном» состоянии покоя, чем другие.
Поскольку с этой точки зрения любое движение может быть только относительным, Эйнштейн выдвинул теорию, которая позже получит название теория относительности. В своей первой работе на эту тему в 1905 году Эйнштейн рассматривал только специальный случай движения с постоянной скоростью; следовательно, данная часть его концепции — это специальная теория относительности.
Затем Эйнштейн произвел второе допущение: скорость света в вакууме, по данным измерений, всегда будет одной и той же независимо от движения источника света по отношению к наблюдателю. (Обратите внимание, что я говорю о скорости «по данным измерений».)
Это постоянство данных измерений скорости света, казалось бы, должно противоречить «фактам», касающимся движения, которые были признаны со времен Галилея и Ньютона.
Предположим, некто бросает мяч мимо нас, мы измеряем горизонтальную скорость мяча относительно нас и находим ее равной x футов в минуту. Если человек находится на платформе, движущейся в противоположном направлении со скоростью y футов в минуту, и бросает мяч с той же силой, его горизонтальная скорость относительно нас должна быть x – y футов в минуту. Если бы платформа двигалась в том же направлении, в котором он бросал мяч, горизонтальная скорость мяча относительно нас должна быть x + y футов в минуту.
И казалось бы, в жизни мы наблюдаем именно такую картину, и измерения подтверждают это. Разве не так должно быть, если человек «бросает» не мяч рукой, а свет фонариком?
Для того чтобы второе допущение Эйнштейна оставалось верным, следует предположить, что эта ситуация не распространяется на свет, да и для мяча-то она на самом деле не такова.
Допустим, что воздействие движения платформы на скорость мяча не так велико, как нам кажется, и что, когда движение платформы добавляется к движению мяча, общая скорость мяча немного меньше, чем x + y. А если движение платформы противоположно движению мяча, то общая скорость мяча немного больше, чем xy. Предположим также, что эта разница возрастает по мере возрастания x и y, но что для скоростей всех материальных тел, которые было возможно наблюдать до 1900 года, эта разница оставалась слишком малой, чтобы ее можно было измерить. Следовательно, мы могли сделать вполне естественный вывод, что общая скорость равна строго x + y или строго x – y и что это верно для всех скоростей.
Но если иметь возможность наблюдать за очень большими скоростями, порядка тысяч километров в секунду, эта разница станет достаточно большой, чтобы ее можно было заметить. Если добавить скорость y к скорости x, общая скорость будет заметно меньше, чем x + y, н будет лишь немногим больше одной скорости x.
Таким же образом, если y вычитается из x, общая скорость будет значительно больше, чем x – y и лишь немного меньше одной скорости x. В конце концов на скорости света воздействие движения источника движущегося тела становится равным нулю, так что x + y = x, и x – y = x независимо от величины y. И это — еще один способ выражения второго допущения Эйнштейна.
Фактически для сохранения этого допущения необходимо складывать скорости таким образом, чтобы их сумма никогда не превышала скорость света. Например, предположим, что платформа движется вперед (по отношению к нам) со скоростью 290 000 км/с, или лишь на 10 000 км/с медленнее скорости света в вакууме. Далее предположим, что с платформы вперед бросают мяч со скоростью 290 000 км/с относительно платформы. Скорость мяча относительно нас должна быть 290 000 + 290 000 км/с при движении вперед, но на этих скоростях влияние движущейся платформы настолько снижено, что общая скорость будет всего лишь 295 000 км/с и все еще остается меньше, чем скорость света.
На самом деле это может быть выражено математически. Если две скорости (V1 и V2) прибавляются друг к другу, то, по Ньютону, их суммарная скорость должна быть V = V1 + V2. По Эйнштейну же, суммарная скорость будет равна:
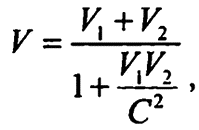
где С — скорость света в вакууме. Если V1 равно С, то уравнение Эйнштейна примет вид:
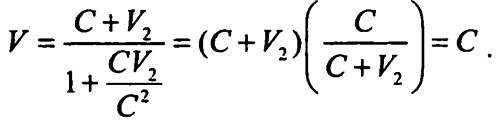
Другими словами, если одна скорость равна скорости света, то добавление к ней другой скорости, даже равной той же скорости света, составит общую скорость, не превышающую скорость света.
Короче говоря, из утверждения Эйнштейна о постоянной измеряемой скорости света можно сделать вывод, что измерение скорости любого движущегося тела всегда покажет величину меньше скорости света[95].
Кажется странным и неудобным принимать такую необычную картину мира только для того, чтобы придерживаться допущения Эйнштейна о постоянности измеряемой скорости света. Тем не менее независимо от того, можно ли измерить скорость света, эта скорость всегда представлялась постоянной, и независимо от того, можно ли измерить скорость движущихся тел, их скорость всегда представлялась меньше скорости света. Короче, еще ни один физик не обнаружил ни одного явления, которое бы нарушало утверждение Эйнштейна об относительности движения или его же утверждение о постоянстве скорости света, а искали они усердно, уж будьте уверены.
Эйнштейн мог вывести из своих утверждений и существование сокращения Лоренца — Фитцджеральда, так же как и описанное Лоренцем приращение массы с движением. Более того, он показал, что не только электрически заряженные частицы прибавляют массу с движением, но и незаряженные частицы тоже. Фактически по мере движения все объекты прибавляют в массе.
Может показаться, что вряд ли есть причина так усиленно вдаваться в специальную теорию. Какая разница, начинать ли с утверждения сокращения Лоренца — Фитцджеральда и из него выводить постоянство скорости света или начинать с утверждения о постоянстве скорости света и выводить из него сокращения Лоренца — Фитцджеральда?
Если бы это было все, то значительной разницы действительно не было бы. Однако Эйнштейн соединил свое допущение о постоянстве скорости света со своим первым допущением об относительности всего движения.
Это означало, что прибавление массы является не «реальным» явлением, а лишь изменением данных измерений. Размер, на который сокращена длина или увеличена масса, не является чем-то определяемым абсолютно, он различается от наблюдателя к наблюдателю.
Чтобы понять, что это означает, представьте себе два одинаковых космических корабля, движущиеся в противоположных направлениях по непересекающейся траектории; на каждом космическом корабле находится оборудование, позволяющее измерить длину и массу другого корабля в то время, как тот пролетает мимо.
С космического корабля X видно, как мимо в определенном направлении пролетает космический корабль Y со скоростью 260 000 километров в секунду, и на этой скорости корабль Y, по данным измерений, имеет только половину своей длины покоя и удвоенную массу сравнительно со своей же массой покоя.
Но люди в корабле Y не чувствуют движения (так же как и мы не чувствуем своего движения сквозь космос вокруг Солнца).
Люди на корабле Y ощущают себя недвижимыми и имеющими длину покоя и массу покоя. А видят они, что мимо них пролетает (в противоположном направлении) корабль X со скоростью 260 000 километров в секунду. Для них именно показатели корабля X изменились на половину длины и удвоенную массу.
Если бы наблюдатели могли общаться между собой во время движения, у них были бы солидные аргументы. Каждый мог бы сказать: «Я нахожусь в покое, а ты движешься. Я нормальной длины, а ты сокращенной. Я имею нормальную массу, а ты — удвоенную».
Так кто же на самом деле «прав»?
Правильный ответ — никто (или оба). Видите ли, вопрос не в том, что «на самом деле» происходит с длиной и массой или какой из кораблей «на самом деле» имеет сокращенную длину или увеличенную массу. Вопрос только в измерении. (Это как — проводя тривиальную аналогию — измерять стороны прямоугольника размером четыре на два метра, а потом спорить, какова «на самом деле» длина прямоугольника — два или четыре метра. Ведь это зависит от того, с какой стороны мерить.)
Но допустим, что вы пытаетесь произвести некий эксперимент, который, предположим, лежит за пределами измерений «реальности». Предположим, например, что вы поставили два корабля рядом и сравнили их напрямую, чтобы выяснить, который из них длиннее и тяжелее. Это на самом деле не может быть произведено в рамках специальной теории Эйнштейна, поскольку она имеет дело только с равномерным движением. Чтобы свести корабли вместе, нужно, чтобы, как минимум, один из них изменил направление движения и развернулся, то есть произвел бы неравномерное или ускоренное движение.
Однако, даже если мы это сделаем и представим оба корабля бок о бок и неподвижными относительно друг друга, после того как они пролетят мимо друг друга на таких суперскоростях, мы не можем делать выводы относительно «реальности». Находясь в покое, каждый из них будет и измерять другого как имеющего нормальную длину и массу. Если и происходило «реальное» изменение длины и массы какого-либо корабля в прошлом, то теперь это изменение исчезло бы без следа.
Несмотря ни на что, сложно перестать думать о «реальности». Тут может помочь воспоминание о том, что были времена, когда мы отказались от иллюзорной «реальности» и с нами не только ничего не случилось, но и адаптировались к жизни мы гораздо лучше.
Так, ребенок очень точно знает, что такое «верх» и «низ». Его голова показывает «вверх», его ноги указывают «вниз» (если он стоит нормально); он прыгает «вверх», он падает «вниз». Более того, вскоре он обнаруживает, что все вокруг него разделяют его мнение по поводу «верха» и «низа».
Если ребенку с такими убеждениями показать глобус, где США находятся вверху, а Австралия — внизу, так что маленькие американцы стоят вверх головой, а маленькие австралийцы — вниз головой, его первой реакцией может быть: «Но это же невозможно! Маленькие австралийцы упадут!»
Конечно, если понимать воздействие силы притяжения (а это понимали задолго до Аристотеля, как минимум, с тех пор, как появилось само представление о Земле, см. ч. I), то бояться, что кто-нибудь упадет с любой части Земли, вы уже не будете. Однако вопрос о природе «верха» и «низа» останется открытым. Вы можете позвонить жителю Австралии по международному телефону и сказать: «Я стою вверх головой, поэтому вы, должно быть, вниз головой». Он ответит: «Нет, нет. Я явно стою вверх головой, стало быть, вниз головой стоите вы».
Видите ли вы, таким образом, насколько бессмысленно спрашивать о том, кто прав и кто «на самом деле» вверх головой? Оба правы, и оба не правы. Каждый стоит вверх головой в рамках собственной системы координат, и каждый стоит вниз головой в рамках системы координат другого.
Большинство людей настолько привыкли к этому, что для них «относительный верх» и «относительный низ» не являются больше нарушениями «здравого смысла». На самом деле именно представление об «абсолютном верхе» и «абсолютном низе» кажется теперь неправильным. Если кто-то всерьез будет утверждать, что австралийцы ходят, будучи подвешенными за ноги, его засмеют.
Если принять принципы релятивистской Вселенной (в как можно более юном возрасте), вышеописанное тоже не будет казаться противоречащим здравому смыслу.
Дата: 2019-07-24, просмотров: 330.