(на примере лесопользования)
Оценка характера лесопользования связана с определённой его формализацией, а для строгого решения задач определения вариантов лесопользования необходима постановка соответствующих задач оптимизации: формулировка цели, общий анализ, обоснование совокупности критериев оптимизации, выбор методов решения задач.
Для формализованного представления лесопользования может быть использовано пространство параметров состояния { X } и управления { Y }. Первые заданы, вторые можно изменять при формировании системы лесопользования. Это деление условно, так как любая группа параметров в зависимости от решаемых задач может характеризовать или состояние системы, или управление ею.
Параметры состояния разделены на независимые, характеризующие общий природно-ресурсный потенциал территории, биологическое разнообразие лесных экосистем, их эколого-экономическую оценку, зависимые производственные и описывающие нормативно-правовую базу многоцелевого лесопользования. Перечень конкретных параметров лесопользования дан на рис. 3.
Значения каждого параметра находятся в определённых пределах, накладываемых условиями существования лесных биоценозов и условиями лесопользования. Все группы параметров взаимосвязаны: в одних случаях установлены вероятностно-достоверные зависимости (например, таблицы хода роста древостоев), в других – логически понятные связи в общем виде (водорегулирующая функция леса), в третьих необходимы специальные исследования (например роль отдельных компонентов леса в задержании техногенных загрязнений атмосферы). Для управления многоцелевым лесопользованием важно знать зависимости параметров экологических последствий от различных вариантов и видов лесопользования. Конкретные виды параметров необходимо представлять в математической форме, т.е. характеризовать вид распределения, его форму, масштаб, взаимозависимость в последовательности, характер динамики во времени и пространстве.

Рис. 3. Параметры системы многоцелевого лесопользования
Качество многоцелевого лесопользования оценивается показателями эффективности (критериями оптимизации), которыми могут быть любые из параметров состояния и управления или характеристики лесопользования, определяемые в зависимости от этих параметров.
Задачи оптимизации лесопользования разнообразны. В общем случае они могут быть разделены на два типа:
· поиск для существующих параметров состояния лесных экосистем { X } оптимальных значений параметров управления лесопользованием { Y };
· поиск для определённых заданных параметров управления лесопользованием {Y } оптимальных значений параметров лесных экосистем { X }.
В задачах первого типа из возможных вариантов организации лесопользования, характеризующихся совокупностью параметров управления (рис. 3), для существующих лесных экосистем с параметрами состояния выбирают такой, при котором критерий оптимальности U получит экстремальное значение. Целевая формула имеет вид:
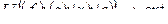 (6)
(6)
при 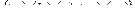 = const.
= const.
В таких задачах среди параметров управления в качестве основных могут быть выделены параметры совершенствования: процесса конкретного вида лесопользования ( s ), лесоперерабатывающего процесса ( r ), финансово-экономической системы ( f ).
При решении конкретных задач выбирают главные параметры, в значительной мере определяющие большую часть остальных. Так, при выборе рационального способа рубки леса в заданных природно-экономических условиях главными являются возрастная структура и тип леса; условиями и ограничениями – расширение площади несплошных рубок. Аналогично формулируется цель в задачах формирования транспортной сети лесопромышленного региона, создания лесопромышленной системы с максимальным использованием древесной массы и др.
В задачах второго типа среди существующих лесных экосистем находят такие, которые при определённых заданных значениях параметров управления обусловят экстремум критерия оптимальности U . Целевая функция имеет вид:
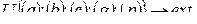 (7)
(7)
при 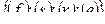 = const.
= const.
В таких задачах доминирует экологический аспект. К ним относятся максимизация углекислогазопоглощающей роли лесов, обоснование возрастов и оборотов рубок леса, размеров главного пользования, программы лесовозобновления с учётом особенностей многоцелевого лесопользования, определение оптимальной залесённости региона и его отдельных зон.
Связь многоцелевого лесопользования с общей системой природопользования заключается в учёте связей лесных экосистем с общими природными комплексами и характера лесопользования с характером других видов природопользования.
Критерии эффективности многоцелевого лесопользования должны быть количественно измеряемыми величинами. Следует исходить из положения, что основной критерий формируется в соответствии со сформулированными выше целями и заключается в производстве определённого (не всегда максимального) количества материальных благ и обеспечении благоприятных условий окружающей природной среды с минимальными совокупными затратами живого и овеществлённого груда.
В общем виде основной критерий оптимизации лесопользования представляется в векторной форме:
U = u (max П; max Э; min З), (8)
где: max П – критерий максимального использования потребительских функций леса, в том числе экологических и социальных;
max Э – критерий максимального обеспечения благоприятных условий окружающей природной среды, соответствующий сохранению биоразнообразия, лесных экосистем;
min 3 – критерий минимума суммарных затрат живого и овеществлённого труда.
Связь многоцелевого лесопользования с общей системой природопользования в критерии (8) осуществляется наложением ограничений на изменение параметров общего природно-ресурсного потенциала территории (а1) < ( ai ) < { an ) ограничений на изменение параметров использования общего природно-ресурсного потенциала ( e 1 ) < (е i ) < (е m ).
Оптимизация по векторному критерию (8) должна выполняться на основе прогнозных расчётов развития лесного комплекса и учёта усиления экологической и социальной роли лесов. То есть основной критерий отражает существование компромисса при решении экономических проблем и охраны окружающей среды.
Наряду с основным критерием для наиболее полной характеристики как отдельных видов лесопользования, так и всей системы многоцелевого лесопользования последовательно вводят дополнительные критерии. Так, критерий эффективного использования потребительских функций леса имеет вид:
max П = и (max P; max S; max С), (9)
где: max Р, max С – критерии максимального использования соответственно сырьевых ресурсов и социальных функций леса;
max S – критерий максимальной реализации защитных функций леса.
Значения параметров, соответствующие оптимальному варианту по данным критериям, должны находиться в определённых пределах, обеспечивающих, в частности, сохранение биологического разнообразия, неистощительности (или постоянства) лесопользования, расширенное воспроизводство лесов и другие условия.
Общие положения однокритериальной оптимизации лесопользования можно разделить на две части: 1) когда наилучший вариант определяется в результате применения строгих математических методов и выражается в однозначной совокупности найденных параметров; 2) когда однозначный результат определить не удаётся. Расчёты показывают, что в большинстве случаев в задачах оптимизации сложных систем характерна пологость изменения критерия оптимальности при приближении к экстремуму.
На рис. 4 дана схема такой ситуации, где при поиске рационального варианта лесопользования по критерию max P получена зона относительно равнозначных вариантов В1, Вi, В6 с мало отличающимися значениями критерия Р1, Рi, Р6, характеризующихся существенно отличающимися совокупностями параметров управления 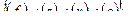 ; …;
; …; 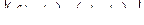 . Эта особенность не позволяет однозначно определить наилучший вариант лесопользования по любому частному критерию. Неопределённость оптимальных решений обусловлена неполным знанием условий будущего функционирования лесных экосистем (особенно после антропогенного воздействия на них); неточностью и недостаточностью исходной информации о связях между параметрами и критериями; устойчивостью экономических и экологических показателей.
. Эта особенность не позволяет однозначно определить наилучший вариант лесопользования по любому частному критерию. Неопределённость оптимальных решений обусловлена неполным знанием условий будущего функционирования лесных экосистем (особенно после антропогенного воздействия на них); неточностью и недостаточностью исходной информации о связях между параметрами и критериями; устойчивостью экономических и экологических показателей.
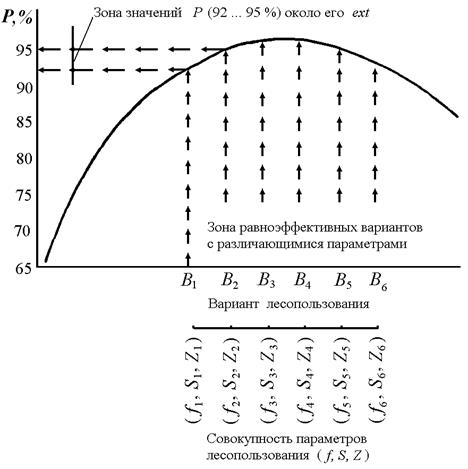
Рис. 4. Схема образования зоны неопределённости оптимальных решений
При наличии зоны неопределённости следует находить возможно более однозначные решения; они основаны на эвристических методах (Оуэн, 1971), в которых используют специальные (дополнительные) критерии. Для задач оптимизации лесопользования приемлемы критерии средних затрат, минимаксных затрат, минимаксного риска. Для определения таких критериев составляют матрицу вариантов многоцелевого лесопользования (рис. 5).
| Варианты лесопользования – параметры управления Y = {f; s; r} | Условия многоцелевого лесопользования – параметры состояния Х = {a; b; c; g , p , f} | ||||
| Х1 | … | Хj | … | Х6 | |
| Y1 | Р11 | … | Р1i | … | Р16 |
| … | … | … | … | … | … |
| Yi | Рi1 | … | Рii | … | Рi6 |
| … | … | … | … | … | … |
| Y6 | Р61 | … | Р6i | … | Р66 |
Рис. 5. Схема матрицы вариантов многоцелевого лесопользования
в зоне неопределённости оптимальных решений
Здесь индекс i означает номер варианта лесопользования в зоне неопределённости, индекс j – номер совокупности параметров управления системой лесопользования. Тогда значения критериев Р располагаются по диагонали матрицы и имеют вид:
Р11, Р22,… Р iJ , …, P 66 (при i = j).
Критерий средних затрат определяют по максимальному из средних значений показателя Р для каждой совокупности параметров (по вертикали):
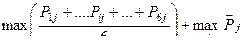 (10)
(10)
При использовании критерия минимаксных затрат выбирают вариант лесопользования, для которого худший результат лучше, чем худший для любого другого варианта:
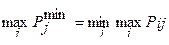 . (11)
. (11)
Этот критерий, по сравнению с критерием (10), страхует от отрицательных последствий при самой неблагоприятной реализации системы управления многоцелевым лесопользованием.
Для особо важных случаев организации лесопользования (например, в лесах защитных категорий) рациональный вариант выбирают по критерию минимаксного риска. Матрица Р ij преобразуется в матрицу рисков Rij согласно соотношению:
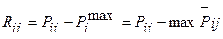 . (12)
. (12)
Смысл этого критерия сводится к устранению риска слишком больших потерь какой-либо функции леса при появлении неблагоприятных условий функционирования лесных экосистем при их многоцелевом использовании.
Таким образом, в результате однокритериальной оптимизации по определённому частному критерию находят оптимальные значения параметров управления многоцелевым лесопользованием; каждый частный критерий выделяет свою совокупность параметров. Поэтому приемлемое решение по векторным критериям (8) и (9) будет соответствовать промежуточным вариантам между вариантами с max П, max Э, min 3 или между вариантами с max P , max S , max С.
Многокритериальные задачи решают путём ранжировки критериев по важности или путём синтеза глобального критерия. В первом случае критерии оптимизации жёстко располагаются в порядке относительной важности или произвольно, но тогда каждому соответствует определённая уступка. Оптимальный вариант многоцелевого лесопользования соответствует экстремальному значению самого важного критерия. При менее жёстком расположении оптимальный вариант полагает отклонение от экстремальных значений частных критериев, т.е. уступки этим критериям. Так, в рациональном варианте лесопользования в лесах промышленной зоны каждому частному критерию max P, max S и max С соответствует определённое отклонение δP, δS и δC.
Поиск рационального варианта ведётся в такой последовательности:
1) найти max P(f1, s1, r1, e1);
2) найти max S(f2, s2 r2, e2), P(f2, s2,r2,e2) ≥ max P(f1 ,s1, r1, e1) - δP; (13)
3) найти max С (f3, s3, r3, e3), P(f3,s3,r3,e3) ≥ max P(f1, s1, r1, e1) - δP;
S(f3,s3,r3,e3) ≥ max S(f2, s2, r2, e2) - δs.
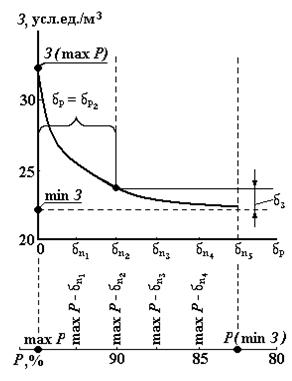
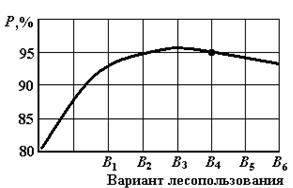
Значения уступок δP, δS и δC определяют через взаимосвязи частных критериев. Так, для определения δS критерию S задают несколько значений δS(1),и δS(2) и определяют соответствующие значения Р(δS(1)), P(δS(2),)... Отсюда становится ясной зависимость δS от Р. На рис. 6 дана графическая интерпретация этой зависимости. Результаты расчётов показывают, что вначале даже небольшие уступки δ3 позволяют получить значительный выигрыш по критерию max P . С дальнейшим увеличением уступки δ3 выигрыш растёт медленнее.
Рассмотренная методология многокритериальной оптимизации в природопользовании позволяет подойти к решению проблемы устойчивого управления лесами, когда обеспечивается должный баланс между решением социально-экономических проблем и сохранением окружающей природной среды. В практическом плане многокритериальная оптимизация лесопользования была применена при поиске эффективной организации, переработки древесных ресурсов на Урале (Лебедев, 1988). Предложены решения по распределению, специализации, концентрации и оптимизаций транспортно-технологических потоков леса, позволяющие из заданного объёма древесных ресурсов получать максимально возможный объём товарной продукции; важным ограничением в решении данной задачи являлось сохранение средоформирующих функций лесов, их экологического потенциала.
| Вариант а | Вариант б |
| 
|
| Вариант в | |
|
| |
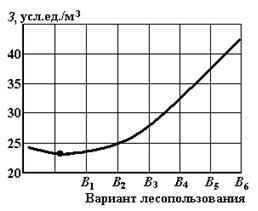
Рис. 6. Графическая интерпретация обоснования уступок критериям
max P и min З:
а – зависимость критерия уровня использования сырьевых ресурсов леса
(P, %) от вариантов лесопользования;
б – зависимость критерия суммарных затрат труда на получение продукции
(З, усл. ед./1м3 древесины) от вариантов лесопользования;
в – зависимость между критериями суммарных затрат труда З и
уровнем использования сырьевых ресурсов леса Р
ГЛАВА 3
Дата: 2019-07-24, просмотров: 381.