Данный вид задач представляет собой сложный вид, т.к. эти задачи студенты решают очень плохо. После объяснения решения таких задач целесообразно порешать аналогичные задачи как индивидуально, так и со всеми вместе (групповым методом).

Для решения задач на смеси и сплавы, на концентрации нужно уметь рассуждать и решать задачи на дроби и проценты, на составление уравнений и их систем. Эти задачи решаются арифметически, применением линейного уравнения и их систем. Рассмотрим задачи, решаемые арифметическим способом.

Приступая к решению задач, связанных с понятиями «концентрация» и «процентное содержание», необходимо объяснить учащимся, что обычно в условиях таких задач речь идет о составлении сплавов, растворов, смесей из двух или нескольких веществ. При решении таких задач принимаются следующие основные допущения:

· Все получающиеся сплавы или смеси однородны;

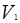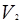· При слиянии двух растворов, имеющих объемы  и , получается смесь , объем которой равен V =  + ;

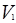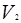· При слиянии двух растворов масса смеси равняется сумме масс, составляющих ее компонентов.

Объемной концентрацией компонента А называется отношение объема чистого компонента ( 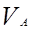) в растворе ко всему объему смеси( ):

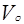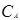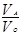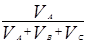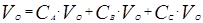= = ,   .                  (5.5.1.)

Объемным процентным содержанием компонента А называется величина (5.5.1), то есть концентрация этого вещества, выраженная в процентах.

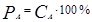                                                    (5.5.2.)

Аналогично определяются массовая концентрация и процентное содержание: отношение массы чистого вещества А в сплаве к массе всего сплава. Под процентным содержанием вещества понимается часть, которую составляет вес этого вещества от веса всего соединения.               

Задача 5.5.3. Для проведения опыта научный сотрудник химической лаборатории смешал 4% раствор некоторого химического вещества и 10% раствора этого же вещества и получил 75 мл. 8% раствора. Сколько миллилитров 4% раствора и сколько 10% раствора было взято.

Решение: Обозначим через x – количество 4% раствора, а через y – количество 10% раствора. Запишем первое уравнение системы, т.к. должно получится 75 мл. раствора:

 x + y=75.

Второе уравнение системы связывает количество соли в 4%, 10% и получившимся растворах:

0,04x + 0,1y =0,08(x+y).

Решим получившуюся систему уравнений:

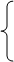x+y=75,

0,04x+0.1y=0,08(x+y);

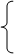x=25,

y=50.

Значит: 25 мл взяли 4% раствора и 50 мл 10% раствора.

Ответ: 25 мл; 50 мл.

Задача 5.5.4. Кусок сплава золота и серебра весом 3 кг содержит 30% золота. Сколько кг чистого золота нужно прибавить к этому куску, чтобы получившийся новый сплав содержал 40% золота?

Решение: Пусть добавили x кг чистого золота;

 3 Х 0,3=0,9(кг) – чистого золота было в сплаве.

 Всего чистого золота стало (x+0,9) кг,

 а сплав массой 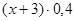 (кг) – чистого золота.

Составим и решим уравнение: 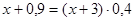, x=0,5, т. е. 0,5 (кг) – надо добавить чистого золота.

Ответ: 0,5 кг.

Задача 5.5.5.  Даны два куска с различным содержанием олова. Первый, массой 300 г, содержит 20% олова, Второй, массой 200 г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?

Решение: До сплавления в двух кусках было 300·20/100+200·40/100=140 г олова. После сплавления кусок массой 200+300=500 г будет содержать 140·100/500 (%) = 28(%) олова. Ответ: 28%.

Задача 5.5.6: Имеется 2 раствора поваренной соли разной концентрации. Если слить вместе 100г первого раствора и 200г второго раствора, то получится 50%-ный раствор. Если же слить вместе 300г первого раствора и 200 г второго, то получится 42%-ный раствор. Найти концентрацию второго раствора.

Решение: Пусть процентное содержание соли в первом и втором растворах p% и q% соответственно, тогда по условиям задачи можно составить два уравнения:

100 p/100 + 200 q/100=50· (100+200)/100

300 p/100 + 200 q/100=42· (300+200)/100.

Упростив эти уравнения и решив систему, получим p=30 и q=60. Следовательно, концентрация второго раствора равна 60%.

Ответ: 60%.

В данной методической разработке рассмотрены основные методы решения задач на проценты и различные задачи на составление уравнений, что является важной частью изучение математики. Здесь рассмотрены задачи на составление « смесей » и на такое понятие как « концентрация ».

       Хочется отметить, что тема работы очень актуальна, тем более в наше время, когда на первое место в отношениях становится экономика, а проценты приобрели широкое распространение в нашей жизни, а в школах уделяется мало время на изучения процентов, да и сам материал рассматривается скупо, не полномасштабно.

       Можно сделать вывод, что эту тему не только можно, но и нужно вводить на факультативных занятиях по математике и на консультациях, а так же отводить время для решения задач на проценты на уроках.

Список использованной литературы :

1. Автономова Т.В. , С.Б. Верченко, В.А. Гусев и др.;25. Практикум по методике преподавания математики в средней школе: Учеб. пособие для студентов физ.-мат. пед. ин-тов/Под ред. В.И.Мишина.– М.: Просвещение, 1993.

2. Виленкин Н.Я. , Жохов В.И., Чесноков А.С. , Шварцбурд С.И. Математика: Учеб. для 6 кл. общеобразоват. учреждений/ . – М.: Мнемозина, 2001

3. Виленкин Н.Я., А.С. Чесносков, и другие. « математика 5 » Москва «просвещение» 2008 г.

4. Дорофеев Г.В., Кузнецова Л.В., Минаева С.С., Суворова С.Б. Изучение процентов в основной школе//Математика в школе. – 2002. – №1 – с. 19 –24.

5. Журнал « Математика » № 3 Москва 2004 г.

6. Журнал « Медицина » Как быть здоровым М.: , 2009

7. Королькова Г.В. . « Методическое пособие по математике » Волгоград 2006 г.

8. Лурье М.В. , Б.И. Александров. « Задачи на составление уравнений».

9. Максимова В.Н. Проблемный подход к обучению в школе Методическое пособие по спецкурсу Л.2003.

10. Матюшкин А.М. Проблемные ситуации в мышлении и обучении М. Педагогика 2007.

11. Поляков С. Зачем нужна математика тем, кому она не нужна? Школьное обозрение. – 2002. – №4. – с. 41 – 43

12. ЕГЭ. 3000 задач с ответами по математике. Под редакцией: А.Л. Семенова, И. В. Ященко. Разработано МИОО. Москва, издательство «Экзамен» 2012 г.

13. Самойлик Г. История математики на уроках. Проценты// Математика. – 2002 – № 36 – с. 3.