Чтобы найти «а» % от числа «в», надо «в» умножить на а/100. Например: 30 % от 60 составляют (60·30)/100=18.

Задача 5.1.1. Число 200 увеличили на 30 %, полученное число увеличили еще на 20 %. Какое число получится в итоге?

Решение:

30 % числа 200 составляют 200*0,3 = 60

Новое число будет 200 + 60 = 260

20 % числа 260 составляют 260 *0,2 = 52

После второго увеличения получим 260 + 52 = 312

Ответ: 312

Задача 5.1.2. Сколько процентов числа 7 составляет разность между ним и 4% числа 28?

Решение:

Найдем 4% от числа 28. Это будет: 28 *0,04 = 1,12.

Определим разность 7 – 1,12 = 5, 88. Найдем, сколько процентов числа 7 составляет 5,88, для этого составим пропорцию:

Число 7 – 100%

 5,88 – х%

Отсюда х =84 %.

Ответ: 84%

Нахождение числа по его процентам.

Если известно, что а% числа «х» равно «в», то число «х» можно найти по формуле х=(в/а)·100.

Например, если 3 % вклада в сберкассу составляют 150 р., то этот вклад равен (150/3)·100=5000 р.

Задача 5.2.1. Некоторое число уменьшили на 12 % и получили 85. Чему равна величина этого числа (с округлением до 0,01)?

Решение: Пусть искомое число х; 12% от х равны 0,12 х, после уменьшения, получим х - 0,12х = 0,88·х= 85 (по условию). Отсюда х=96,590(90). Округлим найденное число до двух знаков после запятой. Так как третья цифра после запятой 0 (меньше 5), то значение второй цифры после запятой сохраняется (в противном случае, эту цифру увеличиваем на 1) х=96,59.

Ответ: 96,59.

Нахождение процентного отношения чисел.

Чтобы найти процентное отношение двух чисел а и в, надо отношение этих чисел умножить на 100 %, т.е. вычислить (а/в) 100%.

Например: при плановом задании 60 автомобилей в день завод выпустил 66 автомобилей, тогда он выполнил план на (66/60) 100 %, т.е. на 110 %.

Задачи на сложные проценты.

Тема «Проценты», связана с повседневной жизнью. Мы часто сталкиваемся с банковскими операциями: различные вклады, ссуды. Между тем, многие студенты, да и взрослые, при столкновении с этими задачами боимся их, потому что не умеем их решать. В учебниках не вводятся формулы простых и сложных процентов. Студенты должны решать задачи, опираясь не на формулы, а на понимание, на смысл понятия «процент», на умение находить процент от числа, число по его проценту. Вообще, данный вид задач применяется во многих областях хозяйственной деятельности и бухгалтерского учёта, а также в различных статистических расчётах, где используются формулы простых и сложных процентов.

Для нахождения простых процентов служит формула простых процентов: если с величины «а» нарастает «р»% за год (или другой период), то через t лет, полученную сумму можно получить по формуле (4.1):

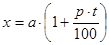                                                 (5.4.1.)

При этом предполагается, что по истечении каждого года доход за этот год исчисляется с первоначальной величины.

Если же доход причисляют к первоначальной величине и, следовательно, доход за новый год исчисляется с наращенной суммы, то говорят о сложных процентах; в этом случае величина, в которую превращается «а» через t лет вычисляется по формуле сложных процентов

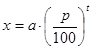                                                     (5.4.2.)

Задача 5.4.3. Клиент положил в банк на год 4000 рублей. Какая сумма у него будет через год, если банк выплачивает 8% годовых?

Решение: Данную задачу можно решить двумя способами.

1 способ. Сначала находим, сколько рублей приходится на 1%:

1) 4000:100=40 ( р.) – на 1%.

Далее находим, сколько рублей будет составлять 8%:

2) 40·8=320 (р.) – на 8%.

А теперь найдём, какая сумма получится в конце года:

3) 4000+320=4320 (р.) – получилась сумма к концу года.

2 способ.

Сначала находим, сколько процентов будет в конце года:

1) 100+8=108% - к концу года.

Находим, сколько приходится на 1%:

2) 4000:100=40 (р.) – на 1%.

А теперь найдём нужную нам сумму:

3) 40*108=4320 (р.) – сумма в конце года.

Ответ: 4320 рублей.

Задача 5.4.4.  Владелец садового участка взял в банке ссуду 300000 рублей для постройки дома на участке. Он должен был вернуть эти деньги через год с надбавкой 9%, какую сумму он должен был вернуть?

Решение:

1) 100+9=109% - должен вернуть в банк владелец.

109:100·300000=327000 (р.) – должен вернуть.

Ответ: 327000 рублей.

Задача 5.4.5. Ирина внесла в январе 100 рублей на счёт, по которому ежемесячно начисляется 2%. И затем каждый месяц в течение года она вносила ещё по 100 рублей, не снимая с него никаких сумм. Сколько рублей на её счете будет в конце декабря?

Решение: Выразим процент десятичной дробью: 2% - 0,02. Вклад ежемесячно увеличивается в 1,02 раза и идёт последовательное накопление вклада:

январь – 100 р.;

февраль – 100·1,02+100 р.;

март – 100· 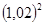+100·1,02+100 р.;

декабрь – 100· (1,02) 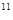+100· (1,02) 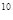+……..+100=100· ((1,02) 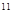+ (1,02) 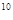+ +1) =100· 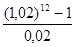=1341(р.)

Ответ: 1341 рубль.

В ходе решения подобных задач учащиеся видят, что формула суммы геометрической прогрессии – это не просто абстракция, отвлечённая формула, а конкретные математическое знание, необходимое в жизни.

Задача 5.4.6.. Вклад, положенный в сбербанк два года назад, достиг 1312500 р. Каков был первоначальный вклад при 25% годовых?

Решение: Пусть x (р.) – первоначальный размер вклада. В конце первого года вклад составит:

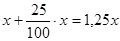 (р.)

1,25 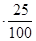 (р.) – на столько увеличился вклад к концу второго года по сравнению с первым;

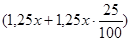 (р.) – таким станет вклад к концу второго года, т.е. составит по условию 1312500 р. Имеем: 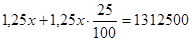, откуда 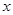=840000. Значит 840000 (р.) – первоначальный вклад.

Ответ: 840000 рублей.