МЕТОДИЧЕСКАЯ РАЗРАБОТКА
по математики
на тему:
«Проценты.
Методика решения задач различных типов на проценты»
Преподаватель математики
Т. Н. Рудзина
Москва
2013
 | |||
 | |||
Содержание.
1. Введение…………………………………………………………… - 2
2. История процентов………………………………………………. - 4
3. Некоторые особенности обучения математике………………. - 6
4. Методика решения задач различных типов на проценты…... - 9
4.1. Методика введения процентов………………………………….. - 9
4.2. Методика нахождения нескольких процентов от числа…….. - 10
4.3. Методика нахождения числа по его процентам………………. - 11
4.4. Методика нахождения процентного отношения………………. - 12
4.5.Задачи на проценты обязательного уровня……………………... - 12
5. Методика изучения процентов при подготовке к ЕГЭ………. .. - 14
5.1.Нахождение числа по его процентам……………………………... - 15
5.2.Нахождение процентов данного числа…………………………..... -16
5.3.Нахождения процентного отношения числа……………………... -16
5.4.Задачи на сложные проценты……………………………………… -16
5.5.Задачи на концентрацию, смеси и сплавы……………………….. -19
6. Заключение…………………………………………………………… -22
7. Список использованной литературы………………... …………… -24
В настоящее время одна из важнейших задач образовательного процесса – обеспечить студентам колледжа глубокие и прочные знания, а также умение рационально применять их в учебной и практической деятельности.
Большое практическое значение имеет умение решать задачи на проценты, потому что понятие процента широко используется как в реальной жизни, так и в различных областях науки.
В школьном курсе эта тема изучается в V – VI классе, но ей отводится очень мало времени и места, в результате учащиеся не умеют решать задачи на проценты. Наблюдения действительно показывают, что многие студенты испытывают трудности, когда встречаются с понятием процента. Студенты колледжа, особенно в начальный период обучения, не разбираются в вопросах инфляции, ценообразования, банковских вкладах и кредитах. Поэтому желательно к этой теме обращаться постоянно, учитывая, что проценты тесно связаны с повседневной жизнью и с ними постоянно приходится иметь дело.
Кроме того, при поступлении в различные институты и университеты требуются знания, связанные с процентами. Сейчас при сдаче ЕГЭ необходимо уметь решать задачи на проценты. При подготовке к экзамену по математике преподавателю предстоит повторить со студентами процентные вычисления, а что-то придётся объяснить заново. Это очень важная работа, так как студенты впервые с процентами знакомились в 5 классе, а в экзаменационных заданиях есть задачи на процентные вычисления.
Задачи на проценты становятся прерогативой экономических дисциплин и химии, которые внедряют свой взгляд на проценты, а в математике их место только в рамках задач на повторение и задач повышенной трудности. Таким образом, студентами колледжа забываются проблемы универсальности процентов и разнообразия сфер их применения.
Тема работы – проценты, точнее будет сказать, их применение в межпредметных связях в колледже для углубленного изучения студентами, для тех, кто хочет поступать в высшие учебные заведения.
Проценты в мире появились из практической необходимости, при решении определенных задач, в основном это экономические потребности. И поэтому надо отметить важность процентов в нашей жизни. Так как проценты проникли практически во все отрасли знаний. Мы не однократно видим, что проценты применяют даже там, где на первый взгляд не применимы так, например человек на вопрос: «Как у Вас здоровье?», - может ответить, что здоров на сто процентов, отсюда видно, что проценты можно применять при измерении не только точных величин, таких как килограммы, рубли и т.д., проценты являются универсальной величиной измерения разных величин и объектов.
Проценты появились в древности, когда появилось понятие долга, так как они нужны были для выплаты по закладным и займам и т. д. И поэтому в математике стала развиваться новая область - проценты. Первая потребность в процентах была экономическая, но затем проценты стали широко применятся в различных отраслях и науках (математика, химия и т д.), и в наше время проценты приобрели широкое распространение.
Определим границы исследований:
предмет – процесс обучения студентов алгоритму решения задач на проценты;
объект - учебная деятельность, при которой студенты учатся решать задачи на проценты.
История процентов
В этом разделе школьной программы 5-го класса хорошо было бы рассказать студентам, напомнить им, об истории возникновения процентов, истории появления на свет знака процента.
При изучении этого материала необходимо напомнить студентам, что такое сотая часть числа (например, сотая часть рубля это копейка).
Необходимо отметить, что люди давно заметили, что сотые доли величин более удобны на практике (например, при записи десятичных дробей).
Итак, слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти». Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Сегодня процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу).
Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента (см. Схему 1, которую можно использовать на уроке).
Схема
1
В учебнике Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова и С.И. Шварцбурда «Математика 5» , в рубрике «История математики» дана еще одна достаточно любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга - руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
В названном учебнике содержатся также достаточно полезные, с точки зрения общего развития, дополнительные сведения, касающиеся промилле (от латинского «с тысячи») – десятой части процента. Сказать студентам колледжа об этом нужно, указав при этом его обозначение ‰.
Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. При этом говорили: «На каждые 100 сестерциев долга заплатить 16 сестерциев лихвы». От римлян проценты перешли к другим народам Европы.
Задача 1.1. Один небогатый римлянин взял в долг у заимодавца 60 сестерциев. Заимодавец поставил условие: «Ты вернешь мне в установленный срок 60 сестерциев и еще 20% от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу, возвращая долг?
Ответ: 72 сестерциев.
Задача 1.2. Некий человек взял в долг у ростовщика 1000 р. Между ними было заключено соглашение о том, что должник обязан вернуть деньги ровно через год, доплатив еще 80% от суммы долга. Но через 6 месяцев должник решил вернуть свой долг. Сколько рублей он вернет ростовщику?
Ответ: 1400 руб.
Задачи на сложные проценты.
Тема «Проценты», связана с повседневной жизнью. Мы часто сталкиваемся с банковскими операциями: различные вклады, ссуды. Между тем, многие студенты, да и взрослые, при столкновении с этими задачами боимся их, потому что не умеем их решать. В учебниках не вводятся формулы простых и сложных процентов. Студенты должны решать задачи, опираясь не на формулы, а на понимание, на смысл понятия «процент», на умение находить процент от числа, число по его проценту. Вообще, данный вид задач применяется во многих областях хозяйственной деятельности и бухгалтерского учёта, а также в различных статистических расчётах, где используются формулы простых и сложных процентов.
Для нахождения простых процентов служит формула простых процентов: если с величины «а» нарастает «р»% за год (или другой период), то через t лет, полученную сумму можно получить по формуле (4.1):
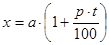(5.4.1.)
При этом предполагается, что по истечении каждого года доход за этот год исчисляется с первоначальной величины.
Если же доход причисляют к первоначальной величине и, следовательно, доход за новый год исчисляется с наращенной суммы, то говорят о сложных процентах; в этом случае величина, в которую превращается «а» через t лет вычисляется по формуле сложных процентов
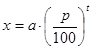(5.4.2.)
Задача 5.4.3. Клиент положил в банк на год 4000 рублей. Какая сумма у него будет через год, если банк выплачивает 8% годовых?
Решение: Данную задачу можно решить двумя способами.
1 способ. Сначала находим, сколько рублей приходится на 1%:
1) 4000:100=40 ( р.) – на 1%.
Далее находим, сколько рублей будет составлять 8%:
2) 40·8=320 (р.) – на 8%.
А теперь найдём, какая сумма получится в конце года:
3) 4000+320=4320 (р.) – получилась сумма к концу года.
2 способ.
Сначала находим, сколько процентов будет в конце года:
1) 100+8=108% - к концу года.
Находим, сколько приходится на 1%:
2) 4000:100=40 (р.) – на 1%.
А теперь найдём нужную нам сумму:
3) 40*108=4320 (р.) – сумма в конце года.
Ответ: 4320 рублей.
Задача 5.4.4. Владелец садового участка взял в банке ссуду 300000 рублей для постройки дома на участке. Он должен был вернуть эти деньги через год с надбавкой 9%, какую сумму он должен был вернуть?
Решение:
1) 100+9=109% - должен вернуть в банк владелец.
109:100·300000=327000 (р.) – должен вернуть.
Ответ: 327000 рублей.
Задача 5.4.5. Ирина внесла в январе 100 рублей на счёт, по которому ежемесячно начисляется 2%. И затем каждый месяц в течение года она вносила ещё по 100 рублей, не снимая с него никаких сумм. Сколько рублей на её счете будет в конце декабря?
Решение: Выразим процент десятичной дробью: 2% - 0,02. Вклад ежемесячно увеличивается в 1,02 раза и идёт последовательное накопление вклада:
январь – 100 р.;
февраль – 100·1,02+100 р.;
март – 100·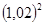 
+100·1,02+100 р.;
декабрь – 100· (1,02)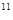 
+100· (1,02) 
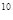+……..+100=100· ((1,02) 
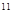+ (1,02) 
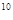+ +1) =100· 
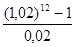=1341(р.)
Ответ: 1341 рубль.
В ходе решения подобных задач учащиеся видят, что формула суммы геометрической прогрессии – это не просто абстракция, отвлечённая формула, а конкретные математическое знание, необходимое в жизни.
Задача 5.4.6.. Вклад, положенный в сбербанк два года назад, достиг 1312500 р. Каков был первоначальный вклад при 25% годовых?
Решение: Пусть x (р.) – первоначальный размер вклада. В конце первого года вклад составит:
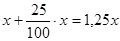(р.)
1,25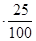 
(р.) – на столько увеличился вклад к концу второго года по сравнению с первым;
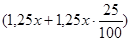(р.) – таким станет вклад к концу второго года, т.е. составит по условию 1312500 р. Имеем: 
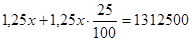, откуда 
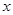=840000. Значит 840000 (р.) – первоначальный вклад.
Ответ: 840000 рублей.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
по математики
на тему:
«Проценты.
Методика решения задач различных типов на проценты»
Преподаватель математики
Т. Н. Рудзина
Москва
2013
| | |||
| | |||
Содержание.
1. Введение…………………………………………………………… - 2
2. История процентов………………………………………………. - 4
3. Некоторые особенности обучения математике………………. - 6
4. Методика решения задач различных типов на проценты…... - 9
4.1. Методика введения процентов………………………………….. - 9
4.2. Методика нахождения нескольких процентов от числа…….. - 10
4.3. Методика нахождения числа по его процентам………………. - 11
4.4. Методика нахождения процентного отношения………………. - 12
4.5.Задачи на проценты обязательного уровня……………………... - 12
5. Методика изучения процентов при подготовке к ЕГЭ………. .. - 14
5.1.Нахождение числа по его процентам……………………………... - 15
5.2.Нахождение процентов данного числа…………………………..... -16
5.3.Нахождения процентного отношения числа……………………... -16
5.4.Задачи на сложные проценты……………………………………… -16
5.5.Задачи на концентрацию, смеси и сплавы……………………….. -19
6. Заключение…………………………………………………………… -22
7. Список использованной литературы………………... …………… -24
В настоящее время одна из важнейших задач образовательного процесса – обеспечить студентам колледжа глубокие и прочные знания, а также умение рационально применять их в учебной и практической деятельности.
Большое практическое значение имеет умение решать задачи на проценты, потому что понятие процента широко используется как в реальной жизни, так и в различных областях науки.
В школьном курсе эта тема изучается в V – VI классе, но ей отводится очень мало времени и места, в результате учащиеся не умеют решать задачи на проценты. Наблюдения действительно показывают, что многие студенты испытывают трудности, когда встречаются с понятием процента. Студенты колледжа, особенно в начальный период обучения, не разбираются в вопросах инфляции, ценообразования, банковских вкладах и кредитах. Поэтому желательно к этой теме обращаться постоянно, учитывая, что проценты тесно связаны с повседневной жизнью и с ними постоянно приходится иметь дело.
Кроме того, при поступлении в различные институты и университеты требуются знания, связанные с процентами. Сейчас при сдаче ЕГЭ необходимо уметь решать задачи на проценты. При подготовке к экзамену по математике преподавателю предстоит повторить со студентами процентные вычисления, а что-то придётся объяснить заново. Это очень важная работа, так как студенты впервые с процентами знакомились в 5 классе, а в экзаменационных заданиях есть задачи на процентные вычисления.
Задачи на проценты становятся прерогативой экономических дисциплин и химии, которые внедряют свой взгляд на проценты, а в математике их место только в рамках задач на повторение и задач повышенной трудности. Таким образом, студентами колледжа забываются проблемы универсальности процентов и разнообразия сфер их применения.
Тема работы – проценты, точнее будет сказать, их применение в межпредметных связях в колледже для углубленного изучения студентами, для тех, кто хочет поступать в высшие учебные заведения.
Проценты в мире появились из практической необходимости, при решении определенных задач, в основном это экономические потребности. И поэтому надо отметить важность процентов в нашей жизни. Так как проценты проникли практически во все отрасли знаний. Мы не однократно видим, что проценты применяют даже там, где на первый взгляд не применимы так, например человек на вопрос: «Как у Вас здоровье?», - может ответить, что здоров на сто процентов, отсюда видно, что проценты можно применять при измерении не только точных величин, таких как килограммы, рубли и т.д., проценты являются универсальной величиной измерения разных величин и объектов.
Проценты появились в древности, когда появилось понятие долга, так как они нужны были для выплаты по закладным и займам и т. д. И поэтому в математике стала развиваться новая область - проценты. Первая потребность в процентах была экономическая, но затем проценты стали широко применятся в различных отраслях и науках (математика, химия и т д.), и в наше время проценты приобрели широкое распространение.
Определим границы исследований:
предмет – процесс обучения студентов алгоритму решения задач на проценты;
объект - учебная деятельность, при которой студенты учатся решать задачи на проценты.
Дата: 2019-07-24, просмотров: 212.
