Заданы пункты потребления – магазины города. Груз необходимо развести из склада агрокомбината «Ждановичи» потребителям. Потребность хозяйств в овощах в напряженный период (3-й квартал) представлена в таблице 3.1. Для удобства введем условные обозначения хозяйств.
Таблица 3.1 – Потребность хозяйств в овощах.
| Наименование хозяйства | Условное обозначение | Потребность, кг |
| ОДО «Артишок» Овощной магазин | 1 | 750 |
| «Гиппо» Гипермаркет | 2 | 695 |
| «Простор» Гипермаркет | 3 | 710 |
| ОДО «Спартак-плюс» | 4 | 900 |
| «Престон» Супермаркет | 5 | 680 |
| Торговый центр «Радзивиловский» | 6 | 615 |
| «Овощи, фрукты» ИП Лотунова. | 7 | 690 |
| «Гиппо» Гипермаркет | 8 | 800 |
| ОАО «Живинка» Магазин №5 | 9 | 645 |
| ОАО «Живинка» Магазин №17 | 10 | 620 |
| ОАО «Живинка» Магазин №24 | 11 | 630 |
Агрокомбинат «Ждановичи» обозначим «0».
Для осуществления доставки овощей потребителям Агрокомбината «Ждановичи» может использовать два собственных транспортных средства марки МАЗ 437040–020 грузоподъемностью 4 т.
Схема размещения хозяйств и расстояния между ними представлена на листе 4 графической части проекта.
Для решения поставленной задачи строим кратчайшую сеть («минимальное дерево»), связующую все пункты без замкнутых контуров (рисунок 3.1).
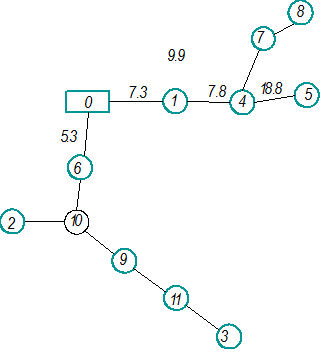
Рисунок 3.1 – Кратчайшая сеть («минимальное дерево»)
Затем по каждой ветви сети, начиная с пункта наиболее удаленного от распределительного центра «0», группируем пункты по маршрутам с учетом:
− количества ввозимого товара;
− грузоподъемности единицы подвижного состава [11].
Исходя из заданной грузоподъемности собственного транспортного средства 4т и количества развозимого груза, все пункты потребления можно сгруппировать в 2 группы (таблица 3.2).
Таблица 3.2 – Группировка маршрутов
| Маршрут 1 | Маршрут 2 | ||
| Пункт | Объем завоза, кг | Пункт | Объем завоза, кг |
| 3 | 710 | 4 | 900 |
| 9 | 645 | 7 | 690 |
| 11 | 630 | 8 | 800 |
| 10 | 620 | 5 | 680 |
| 2 | 695 | 1 | 750 |
| 6 | 615 | – | – |
| Итого | 3915 | Итого | 3820 |
Сгруппировав пункты по маршрутам, определяем рациональный порядок объезда пунктов. Для этого строим таблицу-матрицу (таблица 3.3), в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт «0», а в соответствующих клетках – кратчайшие расстояния между ними.
Рассмотрим маршрут 1.
Таблица 3.3 – Матрица для определения рационального порядка объезда пунктов по маршруту 1
| № | 0 | 8.2 | 14.7 | 13.2 | 12.7 | 15.7 | 8.8 |
| 1) | 8.2 | 3 | 6.5 | 5 | 8.8 | 11.8 | 9.5 |
| 2) | 14.7 | 6.5 | 9 | 4.7 | 5 | 8 | 8.9 |
| 3) | 13.2 | 5 | 4.7 | 11 | 3.8 | 6.8 | 4.5 |
| 4) | 12.7 | 8.8 | 5 | 3.8 | 10 | 3 | 3.9 |
| 5) | 15.7 | 11.8 | 8 | 6.8 | 3 | 2 | 6.9 |
| 6) | 8.8 | 9.5 | 8.9 | 4.5 | 3.9 | 6.9 | 6 |
| Сумма | 73.3 | 49.8 | 47.8 | 38 | 37.2 | 52.2 | 42.5 |
Начальный маршрут строим для трех пунктов матрицы, имеющих наибольшие размеры сумм, показанных в строке (73.3; 52.2; 49.8), т.е. для пунктов 0; 2; 3.
Начальный маршрут: 0 – 2 – 3 – 0. Для включения последующих пунктов выбираем из оставшихся пункт, имеющий наибольшую сумму. Это пункт 9. Далее решаем, между какими пунктами начального маршрута его включить.
Чтобы это решить, для каждой пары пунктов необходимо найти размер приращения маршрута по формуле [11]:
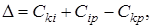 (3.1)
(3.1)
где C – расстояние, км;
i – индекс включаемого пункта;
k – индекс первого пункта из пары;
p – индекс второго пункта из пары.
По формуле 3.1 используя данные таблицы 3.3, рассчитаем размеры приращений.
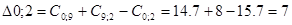
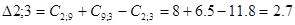
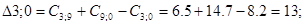
Минимальное значение 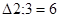 поэтому пункт 9 включаем между 2 и 3. Тогда маршрут примет вид: 0 – 2 – 9 – 3 – 0.
поэтому пункт 9 включаем между 2 и 3. Тогда маршрут примет вид: 0 – 2 – 9 – 3 – 0.
Рассмотрим, между какими пунктами включить пункт 6, так как он имеет наибольшую сумму среди оставшихся.
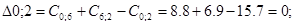
В том случае, когда 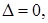 для симметричной матрицы расчеты можно не продолжать, так как значение меньшее, чем 0, получено быть не может.
для симметричной матрицы расчеты можно не продолжать, так как значение меньшее, чем 0, получено быть не может.
Пункт 6 включаем между 0 и 2 и получаем маршрут вида: 0 – 6 – 2 – 9 – 3 – 0.
Рассматриваем пункт 11.
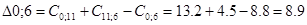
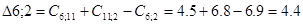
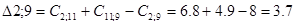
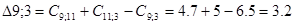
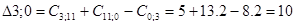
Минимальное значение 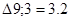 поэтому пункт 11 включаем между 9 и 3. Тогда маршрут примет вид: 0 – 6 – 2 – 9 – 11 – 3 – 0.
поэтому пункт 11 включаем между 9 и 3. Тогда маршрут примет вид: 0 – 6 – 2 – 9 – 11 – 3 – 0.
Рассматриваем пункт 10.
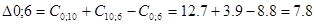
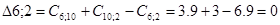
Пункт 10 включаем между 6 и 2,
Получили окончательный маршрут 0 – 6 – 10 – 2 –9 –11 – 3 – 0.
Длина маршрута:
8.8+3.9+3+8+4.7+5+8.2= 41.6 км.
Холостой пробег: 8.2 км.
Рассмотрим маршрут 2.
Таблица 3.4 – Матрица для определения рационального порядка объезда пунктов по маршруту 2
| № | 0 | 6,3 | 14.2 | 16.5 | 11.6 | 4.8 |
| 1) | 6,3 | 4 | 7.9 | 10.2 | 5.5 | 2.1 |
| 2) | 14.2 | 7.9 | 7 | 2.3 | 5.7 | 10 |
| 3) | 16.5 | 10.2 | 2.3 | 8 | 6 | 12.3 |
| 4) | 11.6 | 5.5 | 5.7 | 6 | 5 | 6.8 |
| 5) | 4.8 | 2.1 | 10 | 12.3 | 6.8 | 1 |
| Сумма | 53.4 | 32 | 40.1 | 47.3 | 35.6 | 36 |
Начальный маршрут: 0 – 8 – 7 – 0.
Рассмотрим пункт 1.
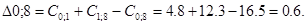
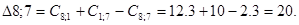
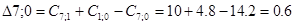
Минимальное значение 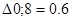 и
и 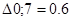 поэтому пункт 1 включаем по своему усмотрению. Пункт 1 включаем между 0 и 8 и получаем маршрут вида: 0 – 1 – 8 – 7 – 0.
поэтому пункт 1 включаем по своему усмотрению. Пункт 1 включаем между 0 и 8 и получаем маршрут вида: 0 – 1 – 8 – 7 – 0.
Рассмотрим пункт 5.
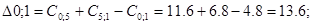
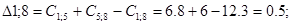
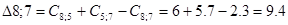
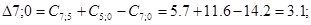
Пункт 5 включаем между 1 и 8, и получаем маршрут вида: 0 – 1 – 5 – 8 – – 7 – 0.
Рассматриваем пункт 4.
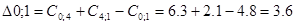
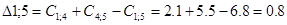
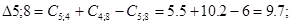
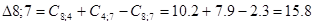
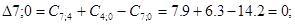
Пункт 4 включаем между 7и 0.
Получили окончательный маршрут 2: 0 – 1 – 5 – 8 – 7 – 4 – 0.
Длина маршрута:
4,8+6,8+6+2,3+7,9+6,3=34,1 км.
Холостой пробег: 6,3 км.
Дата: 2019-04-22, просмотров: 537.