На практике можно провести примеры, когда построенная регрессионная модель оказывается значимой, дисперсии оценок этой модели малы, но модель оказывается неадекватной описываемому процессу. Причина этого может быть в наличии явления автокорреляции - это явление, заключающееся в том, что значения случайной составляющей в любом наблюдении зависит от его значений во всех других наблюдениях. Если в этом случае проанализировать поведение остатков, то зачастую можно выявить следующие тенденции:
● значения регрессионных остатков в соседних точках оказываются одного знака. В данном случае имеет место положительная автокорреляция.
● значения регрессионных остатков в соседних точках оказываются разного знака (по закономерности ). В этом случае имеет место отрицательная автокорреляция остатков.
Явление автокорреляции по поведению остатков можно выявить, если достаточна частота наблюдений. Автокорреляция выявляется с помощью статистики Дарбина- Уотсона:
d= 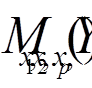
Если наличие автокорреляции отсутствует, то значение статистики должно быть близкой к двум. При наличии положительной автокорреляции величина d близка к нулю (меньше двух); при отрицательной автокорреляции она близка к значению 4. Вычисляют верхнюю 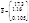 и нижнюю
и нижнюю 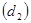 границы для критического значения статистики. Возможны три ситуации:
границы для критического значения статистики. Возможны три ситуации:
1) Если d<d 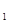 , то делаем вывод о наличии автокорреляции;
, то делаем вывод о наличии автокорреляции;
2) Если d>d 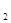 , то нет автокорреляции;
, то нет автокорреляции;
3) Если d 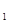
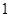 <d<d
<d<d 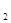 , то в этом случае мы не можем ни принять ни отклонить нулевую гипотезу и анализ осуществляется с помощью нового критерия: d’=4-d.
, то в этом случае мы не можем ни принять ни отклонить нулевую гипотезу и анализ осуществляется с помощью нового критерия: d’=4-d.
В случае наличия автокорреляции ее необходимо устранить, т.к построенные оценки коэффициентов регрессии будут смещенными и состоятельными. В литературе большое внимание уделяется зависимости первого порядка между регрессионными остатками: 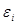 =
= 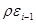 +
+ 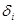 , где
, где 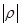 <1;
<1; 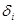 -случайные величины, обладающие свойствоми: М
-случайные величины, обладающие свойствоми: М 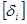 =0; D
=0; D 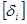 =
= 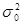 , cov[
, cov[ 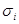 ,
, 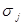 ] =0 при i
] =0 при i 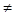 j т.е. относительно
j т.е. относительно 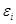 мы имеем линейную регрессионную гомоскедастичную модель. Наша цель- построить ковариационную матрицу вектора регрессионных остатков, найти ее оценку и построить модель ОМНК. Исследуем случайные величины
мы имеем линейную регрессионную гомоскедастичную модель. Наша цель- построить ковариационную матрицу вектора регрессионных остатков, найти ее оценку и построить модель ОМНК. Исследуем случайные величины 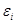 :
:
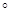 М
М 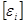 =
= 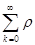
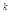 М
М 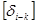 =0
=0
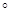 D
D 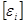 =
= 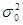
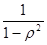 , т.е. дисперсия регрессионных остатков постоянная величина.
, т.е. дисперсия регрессионных остатков постоянная величина.
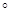
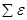 =
= 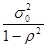
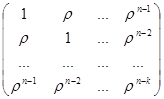
Таким образом, указали вид ковариационной матрицы вектора регрессионных остатков. Для оценки коэффициентов регрессии ОМНК необходимо построить матрицу. Используя вид  можно указать
можно указать  .
.
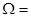
На практике величина 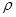 неизвестна. Рассмотрим способом оценивания с помощью метода Кокрейна-Оркатта, который представляет собой итерационный подход, включающий следующие этапы:
неизвестна. Рассмотрим способом оценивания с помощью метода Кокрейна-Оркатта, который представляет собой итерационный подход, включающий следующие этапы:
1. Оценивается регрессия МНК: У=Х 
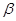 ;
;
2. Вычисляются остатки e 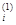 ;
;
3. Оценивается регрессионная зависимость е 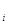 от е
от е 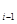 : е
: е 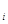 =
= 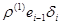 , коэффициент при е
, коэффициент при е 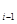 представляет оценку
представляет оценку 
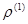 ,
,
4. Строится 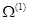 . Используя эту матрицу оцениваем регрессионную зависимость У от Х ОМНК.
. Используя эту матрицу оцениваем регрессионную зависимость У от Х ОМНК.
5. Повторно вычисляют е  процесс возвращается к пункту 3.
процесс возвращается к пункту 3.
Процесс заканчивается, когда значения 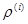 на последнем и предпоследнем этапах будут примерно одинаковыми.
на последнем и предпоследнем этапах будут примерно одинаковыми.
Таким образом указан один из способов построения матрицы 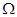 , в случае зависимости регрессионных остатков первого порядка. Используя матрицу
, в случае зависимости регрессионных остатков первого порядка. Используя матрицу 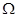 можно построить вектор оценок коэффициентов регрессии ОМНК, проверить на значимость уравнение регрессии, построить доверительные интервалы по вышеописанным формулам
можно построить вектор оценок коэффициентов регрессии ОМНК, проверить на значимость уравнение регрессии, построить доверительные интервалы по вышеописанным формулам
Проверим наличие автокорреляции в модели. Составим расчетную таблицу:
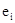
| 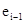
| 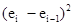
| 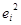
|
| 0.917 2.18 0.808 -5 -7.52 -17.5 7.55 -10.2 11.5 -21.7 2.23 0.909 -7.49 19.7 4.75 -10.3 11.9 10.8 -4.14 -8.63 -6.32 -13.4 -3.89 -5.4 -1.42 19.6 | 2.18 0.808 -5 -7.52 -17.5 7.55 -10.2 11.5 -21.7 2.23 0.909 -7.49 19.7 4.75 -10.3 11.9 10.8 -4.14 -8.63 -6.32 -13.4 -3.89 -5.4 -1.42 19.6 32 | 9,59141 1,88238 33,7329 6,3504 99,6004 627,502 315,063 470,89 1102,24 572,645 1,74504 70,5432 739,296 223,502 226,503 492,84 1,21 223,204 20,1601 5,3361 50,1264 90,4401 2,2801 15,8404 441,84 153,76 | 0,840889 4,7524 0,652864 25 56,5504 306,25 57,0025 104,04 132,25 470,89 4,9729 0,826281 56,1001 388,09 22,5625 106,09 141,61 116,64 17,1396 74,4769 39,9424 179,56 15,1321 29,16 2,0164 384,16 |
Посчитаем критерий Дарбина-Уотсона:
d= 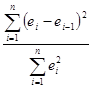 =5998.124/2736.788= 2.191
=5998.124/2736.788= 2.191
Поскольку d>2 то альтернатива отсутствию автокорреляции будет существование отрицательной автокорреляции. По таблице находим для n=27, k=2 (число объясняющих переменных) и уровня значимости a=0,05 : d1=1.24 и d2 = 1.56 Т.к.
4 – d= 1.809 > d2=1.56 следовательно автокорреляции нет.
Дата: 2019-05-29, просмотров: 281.