Устраним мультиколлинеарность методом пошаговой регрессии,
который предполагает, что на каждом шаге мы будем включать в уравнение регрессии тот признак, который будет вызывать наибольшее приращение коэффициента детерминации.
Шаг 1
Строим уравнения регрессии 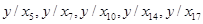
Находим максимальный коэффициент детерминации 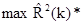 (где k=1)
(где k=1)
Вычисляем нижнюю границу коэффициента детерминации 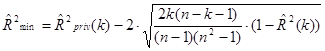 достигнет своего максимума.
достигнет своего максимума.
Используя пакет STADIA определяем:
| Переменная | 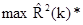
| 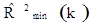
| k |
| X17 | 0.191 | 0.7117 | 1 |
Шаг 2
Строим уравнения регрессии 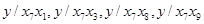
Находим максимальный коэффициент детерминации 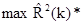 (где k=1)
(где k=1)
Вычисляем нижнюю границу коэффициента детерминации 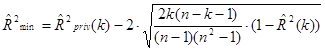 достигнет своего максимума.
достигнет своего максимума.
Используя пакет STADIA определяем:
| Переменная | 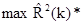
| 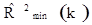
| k |
| X7 | 0.7618 | 0.7117 | 1 |
| Х7,Х9 | 0.8118 | 0.750 | 2 |
Шаг 3
Строим уравнения регрессии 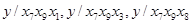
Находим максимальный коэффициент детерминации 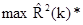 (где k=1)
(где k=1)
Вычисляем нижнюю границу коэффициента детерминации 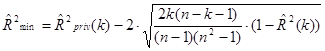 достигнет своего максимума.
достигнет своего максимума.
Используя пакет STADIA определяем:
| Переменная | 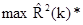
| 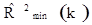
| k |
| X7 | 0.7618 | 0.7117 | 1 |
| Х7,Х9 | 0.8118 | 0.750 | 2 |
| Х7,Х9,X3 | 0.80953 | 0.735 | 3 |
Процесс прекращаем поскольку, 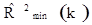 меньше таких коэффициентов для уравнений регрессии с двумя переменными.
меньше таких коэффициентов для уравнений регрессии с двумя переменными.
Подробный анализ, выполненный с помощью программы “Stadia”, приведен в Приложении 1.
Граф.1
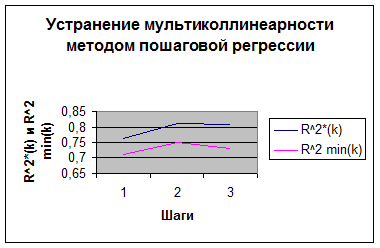
Подробные расчеты см. Приложение 1
Таким образом , из анализа исключаются все факторные признаки,
кроме Х7,X9
2. Проверить построенную модель на гетероскедастичность. Построить обобщенную модель множественной регрессии (случай гетероскедастичности остатков)
Построение и исследование новой модели регрессии.
Вычисление оценок коэффициентов регрессии
Регрессионная модель примет вид:
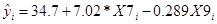
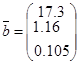
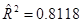
Вывод т.к. 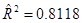 около 1, то можно считать , что связь тесная.
около 1, то можно считать , что связь тесная.
Проверка значимости и построение доверительных интервалов для коэффициентов регрессии
Проверим значимость уравнения регрессии:
H0:<регрессионная модель незначима>
H1:<регрессионная модель значима>
Fвычисленное=57.1
Fкритическое (0,05;2;24)=3,40 так как Fвычисленное > Fкритическое ,
то принимается гипотеза Н1 , следовательно в уравнении коэффициенты регрессии должны быть значимыми.
Проверим значимость коэффициентов регрессии
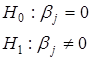 tкритическое =2.064
tкритическое =2.064
tвычисленное = .
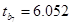 коэффициент значим.
коэффициент значим.
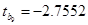 коэффициент значим
коэффициент значим
.
коэффициенты значимы, поскольку 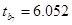 > tкритическое =2.064,
> tкритическое =2.064, 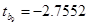 < tкритическое ,
< tкритическое ,
Построим доверительный интервал для коэффициентов по формуле:
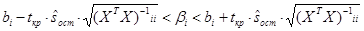
где 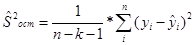 остаточная дисперсия
остаточная дисперсия
Используя пакет STADIA находим доверительный интервал для коэффициента при переменной Х7,Х9.
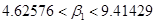
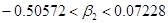
Дата: 2019-05-29, просмотров: 299.