Волновая теория света - одна из теорий, объясняющих природу света. Основное положение теории заключается в том, что свет имеет волновую природу, то есть ведёт себя как электромагнитная волна, от длины которой зависит цвет видимого нами света.

Теория подтверждается многими опытами (в частности, опытом Т. Юнга), и данное поведение света (в виде электромагнитной волны) наблюдается в таких физических явлениях, как дисперсия, дифракция и интерференция света. Однако многие другие физические явления, связанные со светом, одной волновой теорией объяснить нельзя.

Теория берёт своё начало от Гюйгенса. Она рассматривает свет как совокупность поперечных монохроматических электромагнитных волн, а наблюдаемые оптические эффекты - как результат интерференции этих волн. При этом считается, что в отсутствие перехода энергии излучения в другие виды энергии эти волны не влияют друг на друга в том смысле, что, вызвав в некоторой области пространства интерференционные явления, волна продолжает распространяться дальше без изменения своих характеристик. Волновая теория электромагнитного излучения нашла своё теоретическое описание в работах Максвелла в форме уравнений Максвелла. Использование представления о свете как волне позволяет объяснить явления, связанные с интерференцией и дифракцией, в том числе структуру светового поля (построение изображений и голографию).

ИНТЕРФЕРЕНЦИЯ ВОЛН - такое наложение волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн.

Необходимые условия для наблюдения интерференции:

1) волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени (или менялась не очень быстро, что бы её можно было успеть зарегистрировать);

2) волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции (попробуйте сложить две перпендикулярные синусоиды!). Иными словами, складываемые волны должны иметь одинаковые волновые векторы (или близконаправленные).

Волны, для которых выполняются эти два условия, называются КОГЕРЕНТНЫМИ. Первое условие иногда называют временной когерентностью, второе - пространственной когерентностью.

Рассмотрим в качестве примера результат сложения двух одинаковых однонаправленных синусоид. Варьировать будем только их относительный сдвиг. Иными словами, мы складываем две когерентные волны, которые отличаются только начальными фазами (либо их источники сдвинуты друг относительно друга, либо то и другое вместе).

Если синусоиды расположены так, что их максимумы (и минимумы) совпадают в пространстве, произойдет их взаимное усиление.

Если же синусоиды сдвинуты друг относительно друга на полпериода, максимумы одной придутся на минимумы другой; синусоиды уничтожат друг друга, то есть произойдет их взаимное ослабление.

Математически это выглядит так. Складываем две волны:

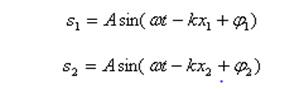
здесь х₁ и х₂ - расстояния от источников волн до точки пространства, в которой мы наблюдаем результат наложения. Квадрат амплитуды результирующей волны (пропорциональный интенсивности волны) дается выражением:

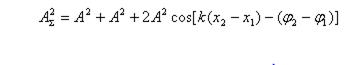
Максимум этого выражения есть 4 A ², минимум - 0; всё зависит от разности начальных фаз и от так называемой разности хода волн D:

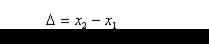
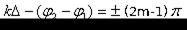При  в данной точке пространства будет наблюдаться интерференционный максимум, при интерференционный минимум.

В нашем простом примере источники волн и точка пространства, где мы наблюдаем интерференцию, находятся на одной прямой; вдоль этой прямой интерференционная картина для всех точек одинакова. Если же мы сдвинем точку наблюдения в сторону от прямой, соединяющей источники, мы попадем в область пространства, где интерференционная картина меняется от точки к точке. В этом случае мы будем наблюдать интерференцию волн с равными частотами и близкими волновыми векторами.

ОПЫТ ЮНГА

Два точечных монохроматических источника (длина волны λ, интенсивность каждого I0) расположены на расстоянии d друг от друга. Найдем, как будет выглядеть интерференционная картина при различных положениях экрана для наблюдений, удаленного от источников на расстояние L>>d.

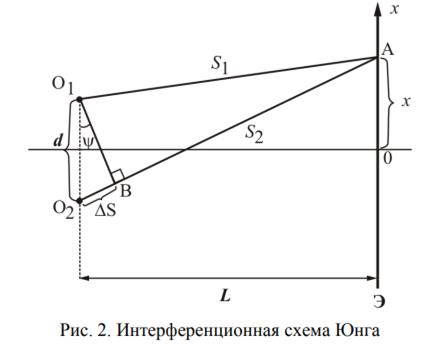
1.Плоскость экрана Э параллельна линии О1О2, соединяющей источники (рис.2). Данное расположение принято называть схемой Юнга. Найдем разность хода ∆s = s2 − s1 между лучами, идущими от источников О1 и О2 в точку А с координатой х:

Френель предложил в качестве двух когерентных источников воспользоваться двумя изображениями одного и того же действительного источника света в двух плоских зеркалах.  Схема опыта Френеля представлена на рисунке,

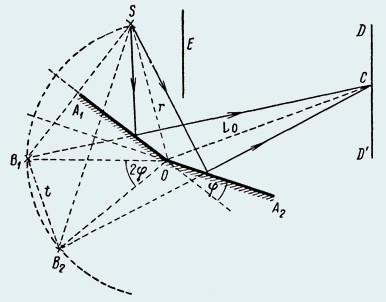
где A₁O и А₂O − два плоских зеркала, расположенных под углом φ; S − источник света, находящийся на расстоянии r от места соприкосновения зеркал в точке О.

Для построения изображений источника S в обоих зеркалах воспользуемся тем, что мнимое изображение, даваемое плоским зеркалом, лежит за зеркалом на таком же расстоянии, на каком объект лежит перед зеркалом. Проведем из точки Оокружность с радиусом r = OS и опустим из точки S перпендикуляр на продолжение прямой ОА₁; точка пересечения продолжения этого перпендикуляра с окружностью В₁ даст изображение источника S в первом зеркале ОА₁. Так же построим изображение В₂ даваемое во втором зеркале ОA₂.

С другой стороны, изображение B₂ лежит в той точке, куда переместилось бы изображение В₁ при повороте первого зеркала ОА₁ на угол φ.

Поэтому <B₁OB₂ = 2φ, и линейное расстояние d между В₁ и В₂ приближенно равно 2φr:

d = 2φr. (1)

Свет от обоих изображений В₁ и В₂ падает на экран DD^/, отстоящий от зеркал на расстоянии L_o. Заслонка Е мешает попадать на экран DD^/ прямому свету от источника S. Так как оба изображения B₁ и В₂ воспроизводят колебания одного и того же действительного источника, то они когерентны, и на экране DD^/ наблюдаются интерференционные полосы. Расстояние между полосами Δl равно

Δl = λL/d,

где L − расстояние от источников до места наблюдения полос.

Подставляя сюда вместо d его значение по (1) и замечая, что приближенно

L = L_o + r,

получим

Δl = (L_o + r)λ/(2φr),

или отсюда

λ = 2φr•Δl/(L_o + r).

Так как в последней формуле все величины, стоящие в правой части, доступны измерению, то из нее видно, что опыт с зеркалами Френеля позволяет измерить длину световых волн λ.

Зеркала в опыте Френеля приходится располагать под весьма малым углом φ друг к другу, так как иначе полосы получаются слишком узкими. Источник света берется в виде узкой щели, параллельной ребру О, образованному зеркалами. При этом интерференционные максимумы имеют вид прямых параллельных полос. При наблюдении в белом свете центральная полоса получается белая (k = 0, усиливаются лучи всех длин волн λ), остальные − окрашенные.

Бипризма Френеля.

Этот опыт представляет собою простой вариант с бизеркалами Френеля.

Свет от источника S преломляется в двух призмах с малыми преломляющими углами A и A^/ (рисунок),

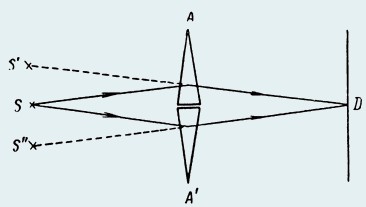
сложенных основаниями.

Призмы отклоняют лучи в противоположных направлениях и, таким образом, возникают два мнимых когерентных источника света S^/ и S^//. Лучи от этих источников, перекрываясь в области D, дают интерференционные полосы.

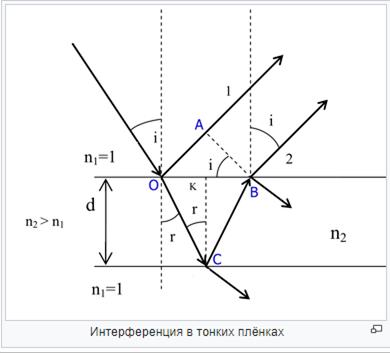
Интерференция в тонких плёнках - явление, которое возникает в результате разделения луча света при отражении от верхней и нижней границ тонкой плёнки. В результате возникают две световые волны, которые могут интерферировать. Тонкоплёночная интерференция объясняет цветовую палитру, видимую в свете, отраженном от мыльных пузырей и масляных плёнок на воде. Это явление также является основополагающим механизмом, используемым в объективах камер, зеркалах, оптических фильтрах и антибликовых покрытиях.

Луч света длиной волны {\displaystyle \lambda } 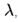, распространяющийся в воздушной среде с показателем преломления {\displaystyle n_{1}=1} 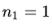при падении на поверхность пленки с показателем преломления {\displaystyle n_{2}>n_{1}} 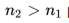разделится на два луча. Часть отражается на верхней поверхности, а часть преломляется. Преломлённый луч достигает нижней границы, затем отражается от нее и снова преломившись, выходит в воздушную среду когерентным с первым лучом. В силу условия когерентности двух лучей наблюдается интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами:

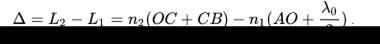
Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 2.15). Роль тонкой пленки, от поверхности которой отражаются волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид окружностей, при наклонном – эллипсов.

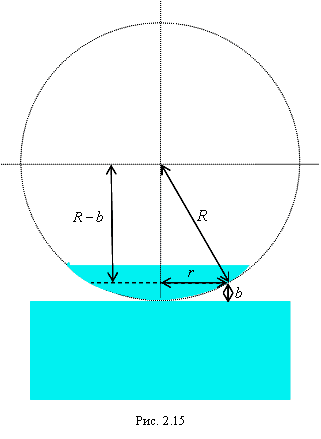
Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. В этом случае 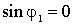и 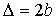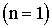. Из рис. 2.15 видно, что 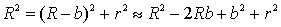, где 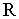– радиус кривизны линзы, 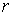– радиус окружности, всем точкам которой соответствует одинаковый зазор 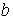. Величиной 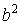можно пренебречь, тогда 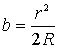. Чтобы учесть возникающее при отражении от пластинки изменение фазы на p, нужно добавить к разности хода :

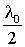В точках, для которых 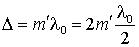, возникнут максимумы интенсивности, а в точках, для которых 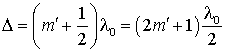– минимумы интенсивности. Оба условия можно объединить в одно:

четным 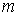будут соответствовать максимумы, а нечетным – минимумы интенсивности. Подставив (2.18) в (2.17), получим радиусы темных и светлых колец Ньютона:

Четным 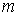соответствуют радиусы светлых колец, нечетным 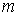– радиусы темных колец. Значению 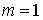соответствует 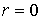, то есть в месте касания пластинки и линзы наблюдается минимум интенсивности, обусловленный изменением фазы на p при отражении световой волны от пластинки.

35. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля. Зоны Френеля.

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом. Независимо от него в 1818 г. французский ученый О. Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.

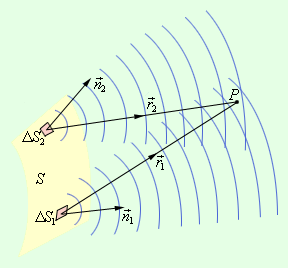
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.

Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS₁, ΔS₂ и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.

Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране (рис. 3.8.2).

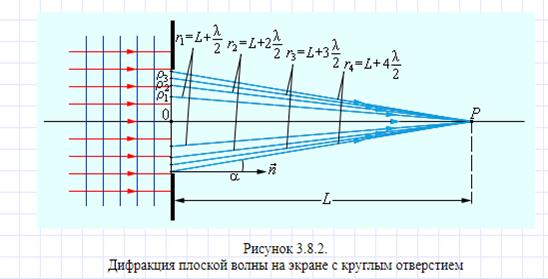
Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A₀падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на половину длины волны, т. е.

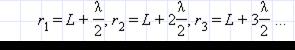
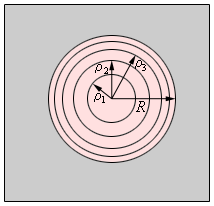
Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).

Рисунок 3.8.3. Границы зон Френеля в плоскости отверстия