Применение теоремы о циркуляции вектора напряженности магнитного поля для расчета напряженности поля соленоида и тороида
Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.
Взаимодействие неподвижных зарядов реализуется посредством электростатического поля. Описывают электростатическое поле при помощи вектора напряженности (E¯), который определен как сила (F¯), действующая на единичный положительный заряд, размещенный в рассматриваемой точке поля:
E¯=F¯q(1).
Электростатические силы являются консервативными, это значит, что их работа по замкнутой траектории (L) равна нулю:
ВВA=∮LF¯dr¯=q∮LE¯dr¯=0ВВ (2),
где r¯ - перемещение.
Интеграл в формуле (2) называется циркуляцией вектора напряженности электростатического поля. Циркуляция вектора E¯- это работа, которую могут совершить силы Кулона, перемещая положительный заряд равный единице по контуру.
Учитывая, что q≠0, получим:
ВВ∮LE¯dr¯=0ВВ (3).
Теорема о циркуляции вектора напряжённости электростатического поля говорит о том, циркуляция E¯ по замкнутому контуру равна нулю.
В дифференциальной форме теорему о циркуляции записывают как:
ВВВВrotВВ E¯=0ВВ (4).
Такой вид записи как (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.
Как следствие из теоремы о циркуляции E¯: работа при перемещении заряда из одной точки поля в другую не зависит от формы траектории движения.
Из теоремы о циркуляции следует, что линии электростатического поля не бывают замкнутыми, они начинаются на положительных, а заканчиваются на отрицательных зарядах.
Соленоид — это провод, равномерно навитый на цилиндрический каркас (рис. 22.5). Будем считать, что диаметр каркаса много меньше его длины, а шаг плотной намотки (расстояние между витками) много меньше диаметра. При этих условиях поле внутри соленоида, как будет очевидно из результата, много больше поля вне соленоида и достаточно однородно (заметим, что поле вне соленоида можно определить по формуле для магнитного поля прямого тока (22.12)). Из соображений симметрии поле внутри соленоида направлено вдоль оси соленоида. Пусть плотность намотки витков (количество витков на единицу длины каркаса) равна п витков на метр.
В соответствии с рис 22.5 выберем прямоугольный контур, у которого малые (по сравнению с большими сторонами длиной /) стороны 2—3 и 4—1 в точке протыкания каркаса перпендикулярны каркасу, большая сторона 1—2 находится внутри каркаса, большая сторона 3—4 находится вне каркаса. В такой ситуации в циркуляции, состоящей из четырех интегралов по отрезкам, доминирует составляющая по отрезку 1—2. Составляющими по отрезкам 2—3 и 4—1 можно пренебречь вследствие малости отрезков. Составляющей по отрезку 3—4 можно пренебречь вследствие перпендикулярности (приблизительно) поля отрезку и малости этого поля. Внутрь контура попадает п! витков с током. Таким образом, циркуляция сводится к отрезку 1—2, но в соответствии с формулой (22.19) определяется полным током nil внутри контура:


Отметим, что это поле достаточно однородно по диаметру каркаса, ведь стороны 2—3 и 4— 1 малы лишь по сравнению с длиной каркаса, но могут быть сравнимы с диаметром каркаса и углубляться внутрь каркаса на любое расстояние.
Соответственно, магнитная индукция внутри длинного соленоида равна

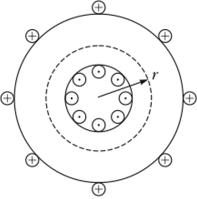
Рис. 22.6
Вычислим теперь магнитное иоле тороида. Тороид — это провод, навитый на тор (бублик). Его можно получить из соленоида, изогнув его в кольцевую катушку (рис. 22.6). Поле тороида похоже на поле соленоида, и линии напряженности тороида параллельны оси тороида. Покажем это, выбрав в качестве контура для вычисления циркуляции окружность радиуса г внутри тора с центром в центре тороида. По теореме о циркуляции для тороида с полным числом витков провода N

откуда магнитное поле внутри тороида

Если контур проходит вне тороида, то внутри него токи отсутствуют, т.е.

и поле из теоремы о циркуляции равно нулю. Таким образом, магнитное поле тороида локализовано внутри тороида и спадает по мере удаления от центра симметрии.
Если тороид тонкий и его радиус R ~ г много больше радиуса витка, то несложно получить, что поле внутри тороида (22.24) дается формулой, аналогичной формуле для поля соленоида (22.22):
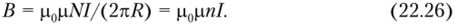
Дата: 2019-05-29, просмотров: 354.