Работа тока - это работа электрического поля по переносу электрических зарядов вдоль проводника; Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работасовершалась.

Тепловое действие тока. Электрический токнагревает проводник. Это явление нам хорошо известно. Объясняется оно тем, что свободные электроны в металлах, перемещаясь поддействием электрического поля, взаимодействуют с ионами или атомами вещества проводника и передают им свою энергию.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов 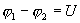, тогда работу по переносу заряда q на этом участке равна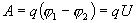

По определению I= q/t. откуда q= I t. Следовательно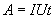

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

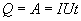
(17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности 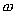, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

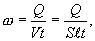
где S - поперечное сечение проводника, 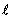- его длина. Используя (1.13) и соотношение 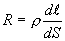, получим

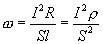
Но 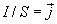- плотность тока, а 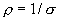, тогда

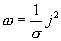
с учетом закона Ома в дифференциальной форме 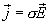, окончательно получаем

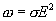
(17.14)

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Для любой точки внутри проводника напряженность 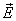результирующего поля равна сумме напряженности поля кулоновских сил и поля сторонних сил 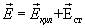. Подставляя в (17.6), получим

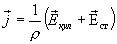
Умножим скалярно обе части на вектор 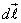, численно равный элементу 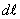длины проводника и направленный по касательной к проводнику в ту же сторону, что и вектор плотности тока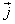

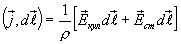
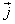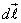Так как скалярное произведение совпадающих по направлению векторов и , равно произведению их модулей, то это равенство можно переписать в виде

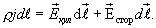
С учетом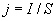

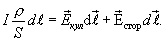
Интегрируя по длине проводника от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинакова, получаем

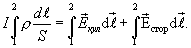
(17.7)

Интеграл 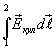численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что

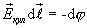
Таким образом,

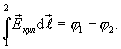
где 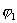и 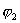- значение потенциала в т.1 и т.2.

Интеграл, содержащий вектор 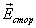напряженности поля, сторонних сил, представляет собой эдс 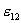, действующей на участке 1-2

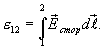
(17.9)

Интеграл

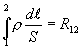
(17.10)

равен сопротивлению участка цепи 1-2.

Подставляя (17.10), (17.9) и (17.8) в (17.7), окончательно получим

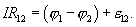
(17.11)

Последнее уравнение выражает собой закон Ома в интегральной форме для участка цепи, содержащего эдс и формулируется следующим образом: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и эдс всех источников электрической энергии, включённых на участке.

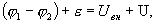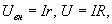При замкнутой внешней цепи сумма падений электрических потенциалов и эдс источника равна сумме падений напряжения на внутреннем сопротивлении источника и во всей внешней цепи где или 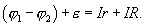Отсюда

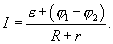
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).

КПД всегда определяем как отношение полезной работы к затраченной:

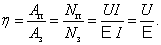
(7.8.1)

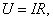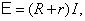Полезная работа – мощность, выделяемая на внешнем сопротивлении Rв единицу времени. По закону Ома имеем: а тогда

.

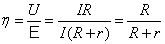Таким образом, имеем, что при 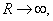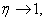но при этом ток в цепи мал и полезная мощность мала. Вот парадокс – мы всегда стремимся к повышенному КПД, а в данном случае нам это не приносит пользы.

Найдем условия, при которых полезная мощность будет максимальна. Для этого нужно, чтобы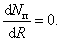

.

.

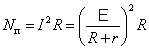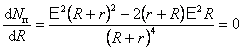(7.8.2)

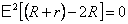
В выражении (7.8.2) 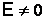, , 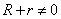следовательно, должно быть равно нулю выражение в квадратных скобках, т.е. r=R. При этом условии выделяемая мощность максимальна, а КПД равен 50%.

Вышесказанное утверждение хорошо иллюстрируется рисунком 7.7.

Как видно из рисунка максимальный КПД получается в данной цепи при уменьшении мощности.

Магнитное действие тока. Магнитостатика вакуума. Элемент тока. Закон Био-Савара–Лапласа и его применение для расчета напряженности магнитного поля прямого бесконечного проводника с током, кольца с током.

Магнитное действие электрического тока

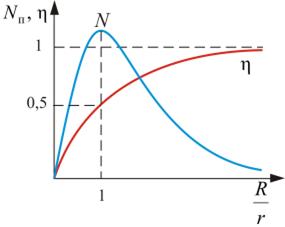
При наличии электрического тока в любом проводнике (в твердом, жидком или газообразном) наблюдается магнитное поле вокруг проводника, то есть проводник с током приобретает магнитные свойства.

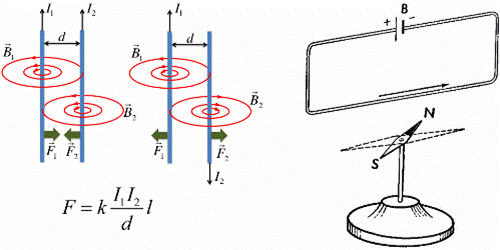
Так, если к проводнику, по которому течет ток, поднести магнит, например в виде магнитной стрелки компаса, то стрелка повернется перпендикулярно проводнику, а если намотать проводник на железный сердечник, и пропустить по проводнику постоянный ток, то сердечник станет электромагнитом.

В 1820 году Эрстед открыл магнитное действие тока на магнитную стрелку, а Ампер установил количественные закономерности магнитного взаимодействия проводников с током.

Магнитное поле всегда порождается током, то есть движущимися электрическими зарядами, в частности - заряженными частицами (электронами, ионами). Противоположно направленные токи взаимно отталкиваются, однонаправленные токи взаимно притягиваются.

Такое механическое взаимодействие происходит благодаря взаимодействию магнитных полей токов, то есть это, в первую очередь, - магнитное взаимодействие, а уж потом - механическое. Таким образом, магнитное взаимодействие токов первично.

Элемент (электрического) тока векторная величина, равная произведению электрического токапроводимости вдоль линейного проводника и бесконечно малого отрезка этого проводника

Закон Био–Савара. Теорема о циркуляции Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). ... Закон Био–Савара определяет вклад в магнитную индукцию результирующего магнитного поля, создаваемый малым участком Δl проводника с током