В цепи, кроме сторонних сил, действуют ещё и электростатические силы: 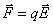. Следовательно, результирующая сила, действующая в каждой точке цепи на заряд q, равна: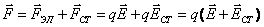  

При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.

   Рис. 1

Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δφ. Разность потенциалов на концах участка 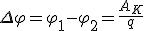, где AK — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению, 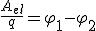, где q — положительный заряд, который перемещается между любыми двумя точками цепи; 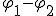— разность потенциалов точек в начале и конце рассматриваемого участка; 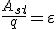. Тогда говорят о напряжении для напряженности: Eстац. э. п. = Eэ/стат. п. + Eстор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:

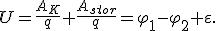
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то 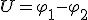. Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.

Закон Ома для неоднородного участка цепи имеет вид: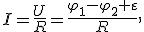

где R — общее сопротивление неоднородного участка.

Расчет разветвленных цепей упрощается, если пользоваться правилами Кирхгофа. Первое правило относится к узлам цепи. Узлом называется точка, в которой сходится более чем два тока. Токи, текущие к узлу, считается имеют один знак (плюс или минус), от узла - имеют другой знак (минус или плюс).

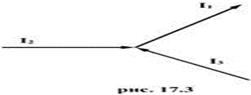
Первое правило Кирхгофа является выражением того факта, что в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды и формулируется в следующем виде: алгебраическая сумма токов, сходящихся в узле, равна нулю

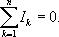
Второе правило Кирхгофа является обобщением закона Ома на разветвленные электрические цепи.

Рассмотрим произвольный замкнутый контур в разветвленной цепи (контур 1-2-3-4-1) (рис. 1.2). Зададим обход контура по часовой стрелке и применим к каждому из неразветвленных участков контура закон Ома.

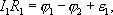
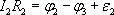
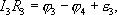
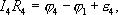
Сложим эти выражения, при этом потенциалы сокращаются и получаем выражение

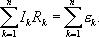
В любом замкнутом контуре произвольной разветвленной электрической цепи, алгебраическая сумма падений напряжений (произведений сил токов на сопротивление) соответствующих участков этого контура равна алгебраической сумме эдс входящих в контур.