Диэлектрики — это вещество, которое не проводит, или плохо проводит электрический ток. Диэлектрическими называют материалы, основным электрическим свойством которых является способность к поляризации и в которых возможно существование электростатического поля.

При внесении диэлектрика во внешнее электрическое поле 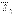в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Связанные заряды создают электрическое поле 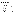которое внутри диэлектрика направлено противоположно вектору напряженности 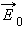внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле 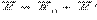внутри диэлектрика оказывается по модулю меньше внешнего поля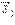

Физическая величина, равная отношению модуля напряженности 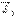внешнего электрического поля в вакууме к модулю напряженности 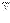полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.

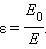
Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, то напряженность поля 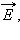создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:

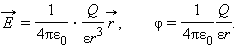
Поток электрического смещения электростатического поля сквозь произвольную замкнутую поверхность, проведенную в поле, равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью.

При расчете полей в среде удобней пользоваться электрическим смещением 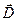, так как оно в отличие от напряженности поля 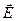не испытывает скачкообразные изменения при переходе через границу диэлектриков.

Вектор

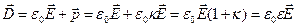
называется электрическим смещением. Размерность [D]=Кл/м 2.

Тогда теорема Остроградского-Гаусса для электростатического поля в диэлектрике запишется в форме

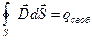
21. Постоянный электрический ток. Сила тока. Плотность тока. Напряжение. Закон Ома для однородного участка цепи в интегральной и дифференциальной формах.

Электрический ток - упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил. Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени.

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

Сила тока - скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

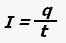
где I - сила тока, q - величина заряда (количество электричества), t - время прохождения заряда.

Плотность тока - векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

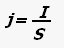
где j -плотность тока, S - площадь сечения проводника.

Напряжение - скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.

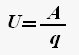
где A - полная работа сторонних и кулоновских сил, q - электрический заряд.

Закон Ома для однородного участка цепи.

Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.

Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)

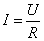
(7.6.1)

Для однородного линейного проводника выразим R через ρ:

,

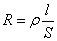(7.6.2)

ρ – удельное объемное сопротивление; [ρ] = [Ом·м].

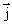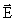Найдем связь между и в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.

В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока 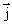и вектор напряженности поля 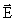коллинеарны (рис. 7.6).

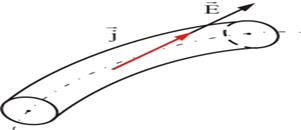
Рис. 7.6

Исходя из закона Ома (7.6.1), имеем:

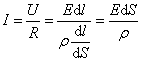
А мы знаем, что 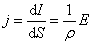или 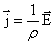. Отсюда можно записать

,

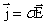это запись закона Ома в дифференциальной форме.