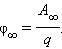Потенциал φ_∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

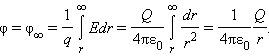
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.

Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.

Рисунок 1.4.3. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.

Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать:

где Δφ = φ₁ – φ₂ – изменение потенциала. Отсюда следует

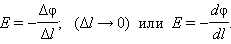
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:

Выше мы познакомились со свойствами электростатического поля: поток вектора напряженности электростатического поля через замкнутую поверхность связан с величиной электрического заряда внутри этой поверхности (теорема Гаусса), а циркуляция вектора напряженности электростатического поля по произвольному неподвижному замкнутому контуру равна нулю (свойство потенциальности). Локальные проявления описанных свойств напряженности электростатического поля выражаются связью дивергенции вектора напряженности 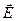с величиной объёмной плотности электрического заряда

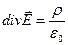(1)

и связью напряженности 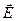с потенциалом электростатического поля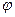 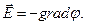(2)

Если второе из рассматриваемых соотношений подставить в первое, можно получить уравнение Пуассона, связывающее потенциал электростатического поля с величиной объёмной плотности электрического заряда:

. (3)

Левую часть уравнения Пуассона обычно записывают с помощью специального оператора «лапласиана скалярной функции»

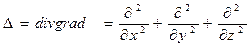. (4)

Если ввести в рассмотрение оператор Гамильтона (другое его название – «оператор набла»)

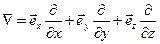, (5)

где 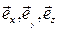- орты декартовой системы координат, то формально дивергенцию вектора 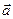можно рассматривать как результат скалярного произведения «вектора» набла на вектор 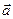, а градиент скалярной функции как произведение «вектора» набла на скаляр, только при этом надо помнить, что оператор набла – дифференциальный оператор - при записи операции должен стоять перед функцией, на которую он действует:

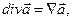
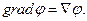(6)

Лапласиан, таким образом, можно рассматривать как последовательное применение оператора Гамильтона (оператора набла):

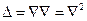. (7)

Итак, уравнение Пуассона для потенциала электростатического поля в вакууме имеет вид:

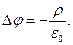(8)

В частном случае, когда объёмная плотность электрического заряда равна нулю, т.е. в рассматриваемой области отсутствуют распределенные по объёму электрические заряды, уравнение Пуассона переходит в уравнение Лапласа

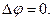(9)

Уравнение Лапласа в электростатике описывает изменение потенциала в пространстве, свободном от электрических зарядов. Значение уравнений Пуассона и Лапласа для изучения электростатических явлений чрезвычайно велико: в отличие от дифференциальной формы теоремы Гаусса эти уравнения - уравнения для единственной неизвестной функции, решение этих уравнений можно получить при самых общих предположениях о характере распределения в пространстве неподвижных и неизменных по величине электрических зарядов. Конкретные результаты получаются с обязательным учетом «граничных условий», т.е. условий, налагаемых на общее решение уравнения Пуассона спецификой рассматриваемой области пространства, свойств замыкающей область поверхности и особенностей распределения электрических зарядов по этой поверхности.

Выражение для лапласиана скалярной функции (4) записано в декартовой системе координат. В цилиндрической системе координат ( 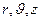) уравнение Пуассона принимает вид

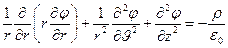, (10)

а в сферической системе координат( ) –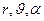

. (11)

В произвольной системе координат можно воспользоваться известными определениями дивергенции вектора и градиента скалярной функции (символическая форма записи).