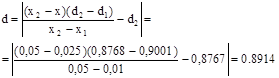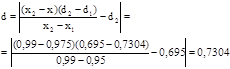На підприємстві з виробництва питних напоїв «Біола» постійно контролюють якість води відповідно до ГОСТ 2874-82 [32].
Одним з контрольованих параметрів є водневий показник рН. Водневий показник виміряється при рН метрі будь-якої моделі зі скляним електродом з похибкою вимірів не перевищуючої 0,1 рН.
Скляний електрод у більшості випадків являє собою трубку з горлового скла, на кінці якої напаяна чутлива мембрана зі спеціального електродного скла [33]. Мембрана виконує функцію одночасно двох водневих електродів: зовнішнього, дотичного з контрольованим розчином, і внутрішнього, дотичного із приелектродній рідиною, що має відому сполуку й певне значення рН. Контакт між обома електродами здійснюється через скляну мембрану, що володіє електричним опором.
Для зняття потенціалу із внутрішньої поверхні скляного електрода служить допоміжний електрод контактної системи.
Таким чином, потенціал скляного електрода є алгебраїчною сумою потенціалів внутрішньої й зовнішньої поверхні вимірювальної мембрани. За умови сталості величини рН приелектродній рідині результуюча э.д.с. скляного електрода буде функцією величини рН контрольованого розчину.
Для виміру показника рН води проводять багаторазові виміри експериментальним шляхом. Данні занесемо у таблицю 5.2.
Таблиця 5.2 ‑ Експериментальні результати вимірювань
| № | 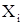
| 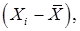
| 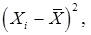
| № | 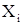
|
| 1 | 6,888 | -0,0106 | 0,00011342 | 1 | 6,881 |
| 2 | 6,910 | 0,0114 | 0,00012882 | 2 | 6,884 |
| 3 | 6,901 | 0,0024 | 0,00000552 | 3 | 6,886 |
| 4 | 6,904 | 0,0054 | 0,00002862 | 4 | 6,888 |
| 5 | 6,913 | 0,0144 | 0,00020592 | 5 | 6,889 |
| 6 | 6,900 | 0,0014 | 0,00000182 | 6 | 6,891 |
| 7 | 6,906 | 0,0074 | 0,00005402 | 7 | 6,891 |
| 8 | 6,894 | -0,0046 | 0,00002162 | 8 | 6,894 |
| 9 | 6,886 | -0,0126 | 0,00016002 | 9 | 6,896 |
| 10 | 6,902 | 0,0034 | 0,00001122 | 10 | 6,900 |
| 11 | 6,881 | -0,0176 | 0,00031152 | 11 | 6,901 |
| 12 | 6,903 | 0,0044 | 0,00001892 | 12 | 6,902 |
| 13 | 6,884 | -0,0146 | 0,00021462 | 13 | 6,903 |
| 14 | 6,889 | -0,0096 | 0,00009312 | 14 | 6,904 |
| 15 | 6,909 | 0,0104 | 0,00010712 | 15 | 6,906 |
| 16 | 6,919 | 0,0204 | 0,00041412 | 16 | 6,906 |
| 17 | 6,906 | 0,0074 | 0,00005402 | 17 | 6,909 |
| 18 | 6,891 | -0,0076 | 0,00005852 | 18 | 6,910 |
| 19 | 6,896 | -0,0026 | 0,00000702 | 19 | 6,913 |
| 20 | 6,891 | -0,0076 | 0,00005852 | 20 | 6,919 |
Результати вважаються незалежними й рівноточними. У загальному випадку вони можуть містити систематичні й випадкову складові погрішності вимірів. Зазначено довірчу ймовірність P=0,95; 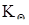 =3,42 – поправковий коефіцієнт.
=3,42 – поправковий коефіцієнт.
За результатами багаторазових спостережень визначити найбільш достовірне значення рН і його довірчі границі.
З результатів спостережень виключити систематичні погрішності не вдається, тому ми їх відносимо до невиключених систематичних погрішностей або до невиключених залишків систематичних погрішностей.
Перевіримо відповідність експериментального закону розподілу результатів спостережень нормальному.
Для цього використаємо 2 критерії згоди.
a) для перевірки гіпотези про нормальність розподілу вихідної серії результатів спостережень за критерієм 1 обчислимо параметр (показник) d, обумовлений співвідношенням
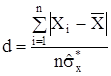 , (5.1)
, (5.1)
де 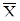 – середнє арифметичне результатів спостережень X,
– середнє арифметичне результатів спостережень X, 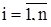
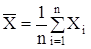 , (5.2)
, (5.2)

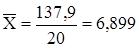 ,
,
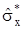 – зміщена оцінка СКВ результатів спостережень Xi
– зміщена оцінка СКВ результатів спостережень Xi
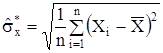 , (5.3)
, (5.3)
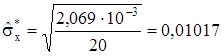 ,
,
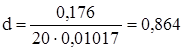 .
.
Результати спостережень 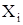 , вважаються розподіленими за нормальним законом, якщо виконується умова:
, вважаються розподіленими за нормальним законом, якщо виконується умова:
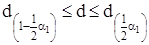 . (5.4)
. (5.4)
Значення -процентних точок розподілу показника (статистики) d
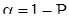 , (5.5)
, (5.5)
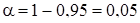 .
.
Одержав квантілі розподілу параметра 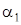 = 0,025 знайдемо показник
= 0,025 знайдемо показник 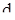 (див. таб. 5.3).
(див. таб. 5.3).
Таблиця 5.3 ‑ Значення показника 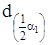
| x1 | x | x2 |
| |
| a | 0.01 | 0.025 | 0.05 | |
| d | 0.9001 | d | 0.8768 |
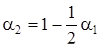 , (5.6)
, (5.6)
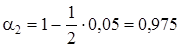 .
.
Одержав квантілі розподілу параметра 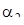 знайдемо показник
знайдемо показник 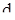 (див. таб. 5.4).
(див. таб. 5.4).
Таблиця 5.4 ‑ Значення показника 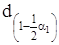
| X1 | X | X2 |
| |
| d | 0.95 | 0.975 | 0.99 | |
| a | 0.7304 | d | 0.6950 |
Тому що розрахункове значення d не виходить за межі теоретичних значень, 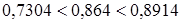 можна вважати, що за першим критерієм розподіл отриманих результатів підкоряється нормальному закону;
можна вважати, що за першим критерієм розподіл отриманих результатів підкоряється нормальному закону;
б) визначимо приналежність результатів спостережень до нормального розподілу по 2 критерію. Відповідно до критерію 2.
Визначаємо число m різностей 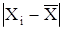 , які перевершують деяке теоретичне значення
, які перевершують деяке теоретичне значення 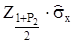 ,
,
де 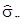 – незміщена оцінка СКО результатів спостережень
– незміщена оцінка СКО результатів спостережень 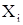
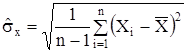 , (5.7)
, (5.7)
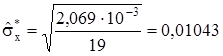 ,
,
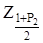 – верхня квантiль розподілу інтегральної функції нормованого нормального розподілу, що відповідає довірчої ймовірності P2. Значення m=1 і P2=0.975 знаходимо по числу спостережень n=20 і рівню значимості
– верхня квантiль розподілу інтегральної функції нормованого нормального розподілу, що відповідає довірчої ймовірності P2. Значення m=1 і P2=0.975 знаходимо по числу спостережень n=20 і рівню значимості 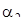 для критерію 2. Потім обчислюємо
для критерію 2. Потім обчислюємо 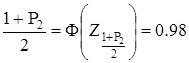 і по табл. П.3 [34] додатка інтегральної функції нормованого нормального розподілу знаходимо
і по табл. П.3 [34] додатка інтегральної функції нормованого нормального розподілу знаходимо 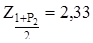 , відповідне вичисленому значенню функції
, відповідне вичисленому значенню функції
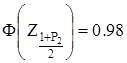 .
.
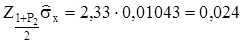 .
.
Аналізуючи значення модулів відхилення 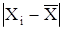 результату спостережень, ми бачимо, що не один з їх не перевищує значення
результату спостережень, ми бачимо, що не один з їх не перевищує значення 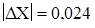 , при m=1, що підтверджує теоретичне допущення.
, при m=1, що підтверджує теоретичне допущення.
Проведемо перевірку грубих погрішностей результатів спостережень.
Для цього: а) складемо впорядкований ряд результатів спостережень, розташувавши вихідні елементи в порядку зростання й виконавши їхню перенумерацію (див. таблицю 5.2);
б) для крайніх членів (результатів спостережень) упорядкованого ряду, які найбільш вилучені від центра розподілу (обумовленого як середнє арифметичне 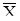 цього ряду) і тому з найбільшою ймовірністю можуть містити грубі похибки, знаходимо модулі різностей
цього ряду) і тому з найбільшою ймовірністю можуть містити грубі похибки, знаходимо модулі різностей 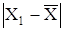 ,
, 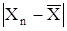 і для більшого з них обчислюємо параметр:
і для більшого з них обчислюємо параметр:
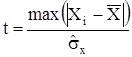 , (5.8)
, (5.8)
де 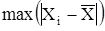 – найбільше значення
– найбільше значення 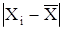 при
при 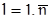
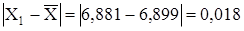 ,
,
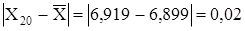 ,
,
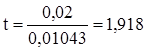 ;
;
в) по таблиці tT (табл. П.7 додатка [34]), входом якої є число елементів вибірки 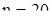 і задана довірча ймовірність
і задана довірча ймовірність 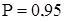 (або рівень значимості a), знаходимо теоретичне або граничне значення параметра
(або рівень значимості a), знаходимо теоретичне або граничне значення параметра 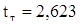 і порівнюємо його з обчисленим фактичним значенням параметра.
і порівнюємо його з обчисленим фактичним значенням параметра.
Критерієм анормальності результату спостережень є умова 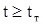 .
.
Одержуємо, що умова не виконалася 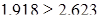 , значить результати вимірів грубих похибок не містять.
, значить результати вимірів грубих похибок не містять.
Обчислюємо незміщену оцінку СКВ результату виміру відповідно до вираження:
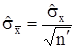 , (5.9)
, (5.9)
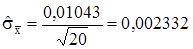 ,
,
де значення незміщеної оцінки СКВ 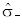 результатів спостережень Xi, обчислено для обсягу вибірки
результатів спостережень Xi, обчислено для обсягу вибірки 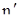 , не утримуючої аномальних (грубих) результатів спостережень. Визначаємо довірчі границі
, не утримуючої аномальних (грубих) результатів спостережень. Визначаємо довірчі границі 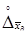 випадкової складової погрішності вимірів з багаторазовими спостереженнями залежно від числа спостережень n у вибірці, що не містить анормальних результатів, границі
випадкової складової погрішності вимірів з багаторазовими спостереженнями залежно від числа спостережень n у вибірці, що не містить анормальних результатів, границі 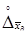 довірчого інтервалу обчислюємо по формулі при n<30:
довірчого інтервалу обчислюємо по формулі при n<30:
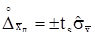 , (5.10)
, (5.10)
де ts=2,09 – коефіцієнт Стьюдента, обумовлений на підставі розподілу Стьюдента по заданій довірчій імовірності Р=0.95 або рівню значимості а й числу ступенів волі Кs= n – 1=19 .
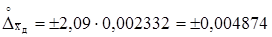
Визначаємо довірчі границі 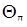 сумарної невиключеної систематичної складової погрішності результату вимірів з багаторазовими спостереженнями.
сумарної невиключеної систематичної складової погрішності результату вимірів з багаторазовими спостереженнями.
Вихідними даними на цьому етапі обробки є границі невиключених залишків систематичних погрішностей, отримані в процесі попереднього аналізу умов проведення експерименту.
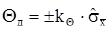 , (5.11)
, (5.11)
де 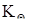 = 3,42 – числовий коефіцієнт, що залежить від довірчої ймовірності Р.
= 3,42 – числовий коефіцієнт, що залежить від довірчої ймовірності Р.
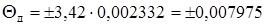 .
.
Визначаємо довірчі границі 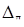 сумарної (повної) погрішності вимірів з багаторазовими спостереженнями.
сумарної (повної) погрішності вимірів з багаторазовими спостереженнями.
Обчислення 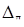 засновано на співвідношенні між СКВ
засновано на співвідношенні між СКВ 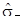 випадковою складовою й довірчими границями
випадковою складовою й довірчими границями 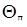 невиключеної систематичної складової погрішності вимірів з багаторазовими спостереженнями. При цьому можливі три випадки з яких ми вибираємо случай при якому
невиключеної систематичної складової погрішності вимірів з багаторазовими спостереженнями. При цьому можливі три випадки з яких ми вибираємо случай при якому 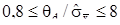 .
.
Для знаходження повної похибки необхідно побудувати композицію розподілу випадкових і невилучених систематичних похибок вимірювань. Проте побудова композиції утруднена, тому використовують емпіричну формулу розрахунку довірчої повної похибки результату вимірювань
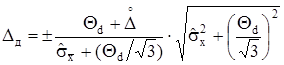 , (5.12)
, (5.12)
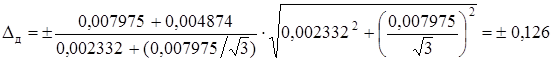 .
.
Записуємо результат вимірів з багаторазовими спостереженнями. Його представляємо у вигляді:
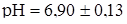 .
.
Дата: 2019-05-29, просмотров: 371.