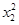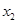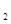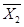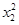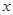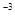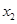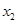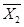Один із шляхів забруднення ропи – це використання у сільському господарстві ядохімікатів. Інше джерело забруднення – це важкі метали. Основна важкість в оцінці наслідків забруднення – важкість розділення привнесених і характерних осаду і ропі кількостей металів.
Судячи з літературних джерел, по токсичній дії метали займають друге місце після ядохімікатів і не виключено, що в майбутньому вони займуть перше місце. Тому очевидна важливість і значимість мір, які попереджують міграцію токсикантів.
Техногеохімічні процеси, пов`язані з внесенням мінеральних добрив і хімічних сполук для захисту рослин, агротехнічні міри обробки землі не можуть не відображатися на складі ропи.
Основним ореолом розсієння є Mn, K, Ca, які є похідними від добрив, Pb, Co, Cu, Ni, Zn – від пестицидів, Mn, Mg, Ca, Co, Cu, K, Zn, Na – кормів для тварин.
Коли ці метали попадають в водне середовище, то або залишаються в решітці потрапивших в воду мінералів, або переходять в розчин, поповнюючи соляний склад води.
В таблиці 8 представлено вміст деяких металів в ропі Куяльницького лиману.
Таблиця 8 – Вміст деяких металі в ропі Куяльницького лиману.
| Назва металу | V | Cu | Mn | Cr |
| т.1 | 0,28 | 0,13 | 0,1 | 0,1 |
| т.2 | 0,28 | 0,07 | 0,04 | 0,13 |
| т.5 | 0,17 | 0,07 | 0,07 | 0,13 |
| т.13 | 0,18 | 0,04 | 0,04 | 0,13 |
| т.14 | 0,17 | 0,17 | 0,07 | 0,13 |
| т.17 | 0,29 | 0,05 | 0,05 | 0,11 |
Коефіцієнт кореляції – це один з найбільш популярних методів математичної статистики.
Коефіцієнт кореляції – це міра взаємозв`язку змінних величин. Він розраховується по спеціальній формулі і змінюється від -1 до +1.
Показники близькі до +1 вказують на те, що при збільшенні однієї змінної, значення іншої теж збільшується і навпаки, якщо показник r близький до -1, то при збільшенні однієї змінної величини, значення іншої зменшується.
Середньоарифметичні значення по металам :
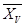 = 1,37 : 6 = 0,23
= 1,37 : 6 = 0,23 

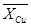 = 0,53 : 6 = 0,09;
= 0,53 : 6 = 0,09;
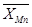 = 0,37 : 6 = 0,06;
= 0,37 : 6 = 0,06;
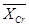 = 0,73 : 6 = 0,12.
= 0,73 : 6 = 0,12.
1) Розрахуємо коефіцієнт кореляції по V – Cu
Таблиця 9 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,28 | 0,13 | 0,05 | 0,04 | 2,5 | 1,6 | 2 |
| 0,28 | 0,07 | 0,05 | -0,02 | 2,5 | 0,4 | -1 |
| 0,17 | 0,07 | -0,06 | -0,02 | 3,6 | 0,4 | 1,2 |
| 0,18 | 0,04 | -0,05 | -0,05 | 2,5 | 2,5 | 2,5 |
| 0,17 | 0,17 | -0,06 | 0,08 | 3,6 | 6,4 | -4,8 |
| 0,29 | 0,05 | 0,06 | -0,04 | 3,6 | 1,6 | -2,4 |
|
|
|
|
| 18,3 | 12,9 | -2,5 |
Коефіцієнт r = 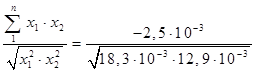 =
= 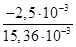 = - 0,16 ;
= - 0,16 ;
2) Розрахуємо коефіцієнт кореляції по V – Mn
Таблиця 10 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,28 | 0,1 | 0,05 | 0,04 | 2,5 | 1,6 | 2 |
| 0,28 | 0,04 | 0,05 | -0,02 | 2,5 | 0,4 | -1 |
| 0,17 | 0,07 | -0,06 | 0,01 | 3,6 | 0,1 | -0,6 |
| 0,18 | 0,04 | -0,05 | -0,02 | 2,5 | 0,4 | 1 |
| 0,17 | 0,07 | -0,06 | 0,01 | 3,6 | 0,1 | -0,6 |
| 0,29 | 0,05 | 0,06 | -0,01 | 3,6 | 0,1 | -0,6 |
|
|
|
|
| 18,3 | 2,7 | 0,2 |
Аналогічно розраховується коефіцієнт кореляції і дорівнює r = 0,028 ;
3) Розраховуємо коефіцієнт кореляції по V – Cr
Таблиця 11 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,28 | 0,1 | 0,05 | -0,02 | 2,5 | 0,4 | -1 |
| 0,28 | 0,13 | 0,05 | 0,01 | 2,5 | 0,1 | 0,5 |
| 0,17 | 0,13 | -0,06 | 0,01 | 3,6 | 0,1 | -0,6 |
| 0,18 | 0,13 | -0,05 | 0,01 | 2,5 | 0,1 | -0,5 |
| 0,17 | 0,13 | -0,06 | 0,01 | 3,6 | 0,1 | -0,6 |
| 0,29 | 0,11 | 0,06 | -0,01 | 3,6 | 0,1 | -0,6 |
|
|
|
|
| 18,3 | 0,9 | -2,8 |
Таким чином, r = - 0,69 ;
4) Розрахуємо коефіцієнт кореляції по Cu – V
Таблиця 12 Розрахунок коефіцієнта корреляції
| X | X | | | | | |
| 0,13 | 0,28 | 0,04 | 0,05 | 1,6 | 2,5 | 2 |
| 0,07 | 0,28 | -0,02 | 0,05 | 0,4 | 2,5 | -1 |
| 0,07 | 0,17 | -0,02 | -0,06 | 0,4 | 3,6 | 1,2 |
| 0,04 | 0,18 | -0,05 | -0,05 | 2,5 | 2,5 | 2,5 |
| 0,17 | 0,17 | 0,08 | -0,06 | 6,4 | 3,6 | -4,8 |
| 0,05 | 0,29 | -0,04 | 0,06 | 1,6 | 3,6 | -2,4 |
|
|
|
|
| 12,9 | 18,3 | -2,5 |
В цьому випадку коефіцієнт r = - 0,16 ;
5) Розрахуємо коефіцієнт кореляції по Cu – Mn
Таблиця 13 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,13 | 0,1 | 0,04 | 0,04 | 1,6 | 1,6 | 1,6 |
| 0,07 | 0,04 | -0,02 | -0,02 | 0,4 | 0,4 | 0,4 |
| 0,07 | 0,07 | -0,02 | 0,01 | 0,4 | 0,1 | -0,2 |
| 0,04 | 0,04 | -0,05 | -0,02 | 2,5 | 0,4 | 1 |
| 0,17 | 0,07 | 0,08 | 0,01 | 6,4 | 0,1 | 0,8 |
| 0,05 | 0,05 | -0,04 | -0,01 | 1,6 | 0,1 | 0,4 |
|
|
|
|
| 12,9 | 2,7 | 4 |
Коефіцієнт дорівнює r = 0,68 ;
6) Розрахуємо коефіцієнт кореляції по Cu – Cr
Таблиця 14 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,13 | 0,1 | 0,04 | -0,02 | 1,6 | 0,4 | -0,8 |
| 0,07 | 0,13 | -0,02 | 0,01 | 0,4 | 0,1 | -0,2 |
| 0,07 | 0,13 | -0,02 | 0,01 | 0,4 | 0,1 | -0,2 |
| 0,04 | 0,13 | -0,05 | 0,01 | 2,5 | 0,1 | -0,5 |
| 0,17 | 0,13 | 0,08 | 0,01 | 6,4 | 0,1 | 0,8 |
| 0,05 | 0,11 | -0,04 | -0,01 | 1,6 | 0,1 | 0,4 |
|
|
|
|
| 12,9 | 0,9 | -0,5 |
Таким чином r = 0,15 ;
7) Розрахуємо коефіцієнт кореляції по Mn – V
Таблиця 15 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,1 | 0,28 | 0,04 | 0,05 | 1,6 | 2,5 | 2 |
| 0,04 | 0,28 | -0,02 | 0,05 | 0,4 | 2,5 | -1 |
| 0,07 | 0,17 | 0,01 | -0,06 | 0,1 | 3,6 | -0,6 |
| 0,04 | 0,18 | -0,02 | -0,05 | 0,4 | 2,5 | 1 |
| 0,07 | 0,17 | 0,01 | -0,06 | 0,1 | 3,6 | -0,6 |
| 0,05 | 0,29 | -0,01 | 0,06 | 0,1 | 3,6 | -0,6 |
|
|
|
|
| 2,7 | 18,3 | 0,2 |
r = 0,028 ;
8) Коефіцієнт кореляції по Mn – Cu
Таблиця 16 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,1 | 0,13 | 0,04 | 0,04 | 1,6 | 1,6 | 1,6 |
| 0,04 | 0,07 | -0,02 | -0,02 | 0,4 | 0,4 | 0,4 |
| 0,07 | 0,07 | 0,01 | -0,02 | 0,1 | 0,4 | -0,2 |
| 0,04 | 0,04 | -0,02 | -0,05 | 0,4 | 2,5 | 1 |
| 0,07 | 0,17 | 0,01 | 0,08 | 0,1 | 6,4 | 0,8 |
| 0,05 | 0,05 | -0,01 | -0,04 | 0,1 | 1,6 | 0,4 |
|
|
|
|
| 2,7 | 12,9 | 4 |
r = 0,68 ;
9) Розрахуємо коефіцієнт кореляції по Mn – Cr
Таблиця 17 Розрахунок коефіцієнта кореляції
| X | X | | | | | |
| 0,1 | 0,1 | 0,04 | -0,02 | 1,6 | 0,4 | -0,8 |
| 0,04 | 0,13 | -0,02 | 0,01 | 0,4 | 0,1 | -0,2 |
| 0,07 | 0,13 | 0,01 | 0,01 | 0,1 | 0,1 | 0,1 |
| 0,04 | 0,13 | -0,02 | 0,01 | 0,4 | 0,1 | -0,2 |
| 0,07 | 0,13 | 0,01 | 0,01 | 0,1 | 0,1 | 0,1 |
| 0,05 | 0,11 | -0,01 | -0,01 | 0,1 | 0,1 | 0,1 |
|
|
|
|
| 2,7 | 0,9 | -0,9 |
r =- 0,58 ;
Відповідно коефіцієнт по іншим парам металів дорівнює :
10 )Cr – V ; r = - 0,69 ;
11) Cr – Cu; r = 0,15 ;
12) Cr – Mn; r = - 0,58.
Коефіцієнт дає змогу оцінити в кількісній формі тільки залежність між двома розглянутими ознаками. В даній роботі використаний метод аналіза, названий «методом ранжування кореляційних профілей», які в наглядній, графічній формі розкривають загальну картину взаємозв`язків між різними елементами.
На основі даних про склад елементів в ропі Куяльницького лиману розраховані коефіцієнти кореляції для всіх можливих пар елементів в даній групі. Далі для кожного елемента всі значення його парних коефіцієнтів кореляції з іншими елементами розміщують в вигляді зростаючого ряда числових значень. Таку послідовність значень коефіцієнта кореляції умовно називають рядом ранжированних величин зв`язку між елементами або просто ранжированими кореляційними профілями.
Таблиця 18 Матриця парних коефіцієнтів кореляції, які оцінюють силу зв`язку між елементами в ропі Куяльницького лиману
| метал | коефіцієнти кореляції | |||
| Cr | Mn | Cu | V | |
| Ванадій | -0,69 | 0,028 | -0,16 | 1 |
| Мідь | 0,15 | 0,68 | 1 |
|
| Марганець | -0,58 | 1 |
|
|
| Хром | 1 |
|
|
|
 Таблиця 19 Ранжування величини сили зв`язку між елементами в ропі Куяльницького лиману
Таблиця 19 Ранжування величини сили зв`язку між елементами в ропі Куяльницького лиману
| Елемент | Ранг | ||
| 1 | 2 | 3 | |
| Ванадій | -0,69 | -0,16 | 0,028 |
| Мідь | -0,16 | 0,15 | 0,68 |
| Марганець | -0,58 | 0,028 | 0,68 |
| Хром | -0,69 | -0,58 | 0,15 |
Дані таблиць свідчать про наявність значимих кореляційних зв`язків деяких елементів. Але структура цих зв`язків між елементами поки залишається невідомою. Для того, щоб її розкрити, переносять кожний ряд ранжированних величин сил зв`язку на координатну площину, в якій для кожного елемента будують свій ранжирований кореляційний профіль, що показує загальну картину взаємозв`язків елементів.
Графіки відображають на площині структуру взаємозв`язків між елементами в ропі Куяльницького лиману.
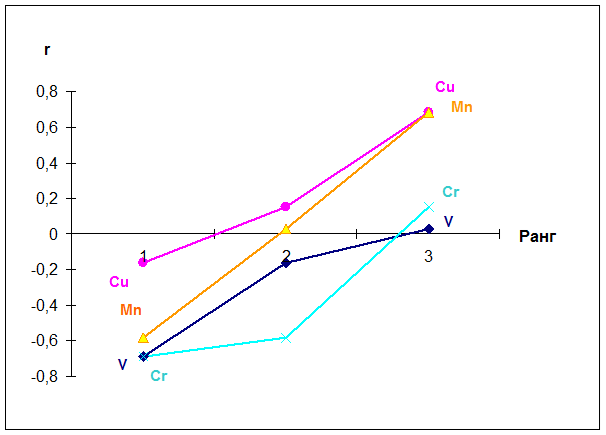 |
Чим ближче один до одного ранжировані кореляційні профілі і схоже їх розташування на цій площині, тим більш узгоджені концентрації елементів в досліджуваному об`єкті і тим більш схожий характер поводження цих елементів, а саме, тим більше є основ віднести їх до однієї геохімічної асоціації.
Рис.4 - Графік ранжированних величин сил взаємозв`язку елементів ропи Куяльницького лиману
При аналізі ранжированних величин сил зв`язків між елементами в ропі Куяльницького лиману можна відмітити, що такі елементи, як мідь і марганець, ванадій і хром утворюють свої геохімічні асоціації і не пов`язані з елементами другої асоціації.
Таким чином, графік ранжированних кореляційних профілей дозволяє, на основі статистичних залежностей між характерами розподілення концентрацій 4 елементів в ропі Куяльницького лиману, поділити всю сукупність елементів наступним чином :
(мідь-марганець) – (ванадій-хром), а саме, виявити дві геохімічні асоціації із 4 елементів.
Хімічні елементи здатні міняти характер розподілення своїх концентрацій від концентрацій інших елементів.
Проведені досліди свідчать про те, що в залежності від природних і техногенних факторів ропа відрізняється по складу металів. Контроль за їх вмістом має велике прикладне значення для оцінки геохімічних процесів, протікаючих в грязевих водоймах, а також виявлення антропогенного навантаження.
Що стосується антропогенного навантаження, то в забрудненні південної частини Куяльницького лиману значна роль належить каналізаційним, промисловим, господарським і побутовим стокам. В лиман поступають промислові та господарсько-побутові стоки Куяльницького заводу мінеральних вод, який знаходиться поруч з курортом Куяльник. Також в лиман скидають післяпроцедурні стоки курорту Куяльник. А контроль за виконанням вимог, які висуваються до округу санітарної зони, має здійснювати ГРЕС (Гідрогеологічна режимно-експлуатаційна станція).
Ступінь самостійності
Об'єктом досліджень був екологічний стан ропи Куяльницького лиману. За результатами дипломної роботи виконано:
— збір теоретичного матеріалу;
— аналіз результатів фізико-хімічних досліджень ропи та грязьового розчину;
— розрахунок макроскладу ропи;
— розрахунок коефіцієнтів кореляції металів в ропі.
По результатам виконання досліджень зроблено висновки.
Новизною даної розробки є комплексний підхід, який дає змогу здійснення адекватного контролю якості ропи згідно вимог чинного законодавства та нормативно-методичної бази. У зв'язку з необхідністю збереження лікувально-рекреаіційної бази України, тема є актуальною. Отримані дані сприятимуть рішенню поставлених задач.
Дата: 2019-05-29, просмотров: 409.
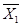
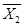
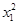
 10
10 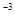
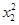
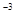
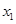
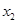
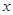
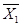
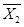
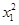
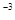
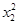
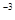
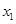
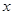
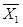
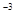
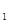
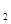 =X
=X 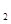 -
- 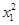
 10
10