За останні роки прикладна реологія дисперсних систем одержала значний розвиток в роботах вітчизняних і зарубіжних учених. Роботами академіка П.А. Ребиндера і його школи були закладені основи нового напряму - фізико-хімічної механіки.

Розуміння фізичного єства поведінки матеріалу при його обробці в робочих каналах механічного устаткування дає вивчення його реакції на дію різних зусиль і їх комбінацій, у тому числі об'ємного стиснення, одноосного розтягування, простого зсуву, стиснення із зсувом.

Матеріал, що переробляється, як відомо, може знаходитися в твердому, рідкому, газоподібному станах і проявляти при деформації в'язкі, пластичні, в'язко-пластичні, пружні, в'язко-пластично-пружні властивості. У кожному конкретному випадку важливо знати характер зв'язку прикладених зусиль і деформації матеріалу, що виникає в робочому каналі машини.

Більшість вологомістких дисперсних систем проявляє під навантаженням як в'язкі, так і пластичні властивості. Пластичні властивості матеріалів вивчають за допомогою моделі реології Сен-Венана. Пластичним тілом Сен-Венана називають тіло, деформація (течія) якого під дією прикладеної напруги відсутня, якщо напруга не досягає певної для даного матеріалу величини, званої межею текучості τ₀. Причому, якщо навантаження на матеріал досягне межі текучості, процес деформації проходить вже незалежно від всіх інших умов (наприклад, від швидкості деформації). Встановити співвідношення між величиною і швидкістю деформації і прикладеною напругою не вдається, можна лише констатувати умову настання стану текучості - пластичності матеріалу (мал.6.19).

При 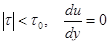 - деформація відсутня, градієнт швидкості рівний нулю.

При 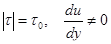 - відбувається перебіг матеріалу.

Графік "перебігу" тіла Сен-Венана представлений прямою лінією (мал.6.19), паралельної осі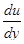

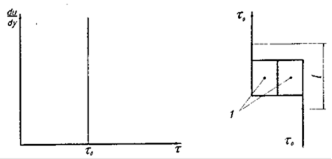
Мал.6.19. Графік течії і модель реології тіла Сен-Венана

Більшість початкових мас для виробництва будівельних матеріалів - вологомісткі дисперсні системи - проявляють під навантаженням в'язко-пластичні властивості.

В 1881 р. шведів, а в 1919 р. Бінгам запропонували метод оцінки пластичних властивостей оброблюваного матеріалу, що одержав назву методу Шведова-Бінгама.

Згідно їх уявленням

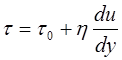 (6.39)

де τ - напруга зсуву в сталому "потоці" матеріалу в робочому каналі, Н/м²; τ₀ - "межа текучості" ("гранична напруга зсуву", яка необхідна створити, щоб почався перебіг матеріалу в робочому каналі машини), Н/м²; η - коефіцієнт в'язкості, що характеризує внутрішнє тертя матеріалу, Н-с/м; 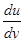 - градієнт швидкості сталої течії в робочому каналі, с-1.

В'язко-пластичні середовища згідно концепції Шведова-Бінгама, на відміну від ньютонівських, не зазнають видимих деформацій до тих пір, поки напруга зсуву не перевищить деякого значення, званого межею текучості.

Таким чином, істинно в'язкі матеріали відрізняються від пластичних тим, що у в'язких відсутня гранична напруга зсуву τ_о і вони "течуть" навіть під впливом власної тяжіння.

Як показує практика, більшість будівельних матеріалів при їх використовуванні разом з вязкопластичними проявляє і пружні властивості.

Згідно дослідженням П.А. Ребіндера, Н.В. Міхайлова, всі системи, що піддаються механічним діям, можна розділити на рідкообразні і твердообразні. До рідкообразних відносяться ньютонівські рідини і структуровані системи, що не мають граничної напруги. Для цих систем τ₀ = 0. До твердообразних тіл - в'язко-пластичні, в'язко-пружні, в'язко-пластично-пружні системи, що володіють граничною напругою зсуву.

Експериментальні роботи, проведені з в'язко-пластичними дисперсними матеріалами зниженої вогкості показали, що у принципі вони поводяться під навантаженням аналогічно структурованим рідинам з малою концентрацією дисперсної фази.

"Кривий перебіг" реологій твердообразних систем в загальному випадку може бути представлені таким чином (мал.6.20).

Якщо здвигові зусилля не перевищують межі міцності просторової структури матеріалу, що деформується, то відбувається повільний рух середовища з постійною найбільшою в'язкістю. Дуже повільний рух матеріалу йде без руйнування структури або з частковим її руйнуванням і одночасним відновленням.

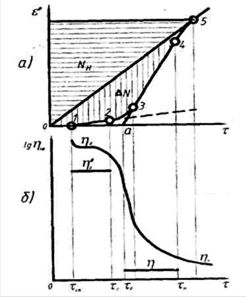
Рис.6.20. Криві реологій для твердообразных систем: а) - залежність градієнта швидкості від напруги зсуву; б) - залежність логарифма ефективної в'язкості від напруги зсуву: 0-1 - зона пружних деформацій; 1 - 2 - зона пластичного тертя з найбільшою в'язкістю: 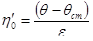 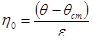- найбільша пластична в'язкість по Шведову; 2-3 - початок зони лавинного руйнування структури; 3-4 - зона в'язкопластичної текучості:  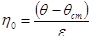- якнайменша пластична в'язкість по Бінгаму; 5 - зона ньютонівської течії з постійною в'язкістю гранично зруйнованої структури.

Ця область 1-2 називається Шведовською областю пластичної течії з найбільшою в'язкістю

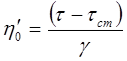. (6.40)

де τ_ст - умовно-статична межа текучості, гранична напруга зсуву, відповідна первинному руйнуванню структури; γ - градієнт швидкості;

2-3 - зона лавиноподібного руйнування структури;

3-4 - зона в'язкопластичної течії з якнайменшою пластичною в'язкістю по Бінгаму

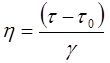 (6.41)

4-5 - зона ньютонівської течії з постійною в'язкістю гранично зруйнованої структури.

Визначення властивостей реологій оброблюваних в'язких і в’язкопластичних матеріалів здійснюється на капілярних вискозиметрах і реометрах різних конструкцій.

Капілярний вискозиметр є циліндровим каналом (капіляр) і системою вимірювання витрати матеріалу - (q) і тиск - (р), продавлюючого через нього досліджуваний матеріал. По набутих значеннях q і p визначають головні характеристики "потоку" - напруга зсуву (τ) або в'язкість (μ) у функції градієнта швидкості (γ). Довжина капіляра повинна бути достатньою, щоб на значній його частині існував сталий профіль швидкостей.

Суть ротаційної вискозиметрії полягає у визначенні зв'язку напруги зсуву на поверхні внутрішнього циліндра з градієнтом швидкості на тій же поверхні.

Ротаційний вискозиметр придатний для вимірювання в'язкості ньютонівських рідин, пластичних дисперсних систем, розплавів полімерів.

Для числового визначення параметрів реологій високов'язких пластичних матеріалів розроблені прилади і методи. Проте через специфічні властивості в'язко-пластичних матеріалів ці прилади часто виявляються непридатними для досліджень реологій. Характеристику реології в'язко-пластичного матеріалу, як правило, одержують у вигляді графіка залежності в'язкості (або напруги зсуву) від градієнта швидкості. З точністю, достатньою для інженерних цілей, можуть бути одержані відомості про поведінку матеріалу в процесі деформації, якщо скористатися поняттям ефективної (аномальної) в'язкості.

Аномалія в'язкості була знайдена Ф.Н. Шведовым і полягала в тому, що заміряна в'язкість зменшувалася із збільшенням градієнта швидкості всупереч існуючому уявленню про постійність цього коефіцієнта у формулі Ньютона.

Поняттям ефективної в'язкості дуже зручно користуватися, оскільки це дає можливість замість 20 критеріїв, що описують поведінку в'язко-пластичних матеріалів при їх деформації, користуватися практично залежністю .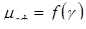

Для спрощення висновків розрахункової залежності допускають μ_эф = const, тобто що коефіцієнт μ_эф відображає деяке "середнє" значення в'язкості, визначуване деяким "середнім" значенням градієнта швидкості "потоку" середовища в робочому каналі (γ_{ср. э}), утворене впливаючими на середовище стінками елементів машин. Таке "усереднювання", безумовно, позначається на точності розрахунків. Проте, для визначення енергосилових параметрів формуючих машин вага більше вживання знаходить практика характеристики властивостей реологій оброблюваних матеріалів залежністю 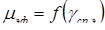. Одержані у такий спосіб розрахункові результати добре співпадають з експериментальними даними, і точність одержаних розрахункових рівнянь в основному залежить від точності визначення характеристик реологій в'язко-пластичної маси, що переробляється.

Повна крива реології пластичної глини може бути побудована за допомогою лабораторних установок, які відповідають фізичним моделям реальних машин. Як такі установки були використані лабораторні вальці, прес з конусом і глинорозтирачем. Попередні теоретичні дослідження показали, що зміна величини зусиль розпорів у вальцях, тиску і витрати оброблюваного матеріалу в конусній головці стрічкового пресу, максимального тиску на стінці глинорозтирача пропорційні зміні в'язкості глиномасси і геометричним параметрам робочого каналу установки.

Розрахувавши для кожного випадку градієнт швидкості і побудувавши графік залежності "в'язкість - градієнт швидкості" для кожної машини, можна шляхом порівняння цих графіків зробити висновок про достовірність пропонованої методики. Збіг набутих значень в'язкості при відповідних значеннях градієнтів швидкості для всіх трьох установок підтвердив положення, згідно якому властивості реологій пластичних глин можуть характеризуватися кривій реології в координатах 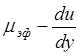 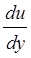- градієнт швидкості перебігу оброблюваного матеріалу.

На мал.6.21 представлений графік залежності ефективної в'язкості від градієнта швидкості глини, одержаний на моделях вальцов і преса. Як видно з графіка, обидві криві, одержані на моделях різних машин, достатньо близькі один до одного.

На мал.6.22 показаний графік залежності в'язкості від градієнта швидкості Кембрійської глини в інтервалі їх формувальної вогкості в діапазоні градієнтів швидкостей роботи глинооброблюючого устаткування. Графік побудований в логарифмічних координатах, в яких залежність 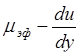 - є прямою лінією.

Для математичного опису цієї графічної залежності найбільш придатне статечне рівняння вигляду

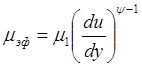 (6.42)

Параметр ψ може бути легко знайдений з графіка, оскільки тангенс кута нахилу прямої рівний (ψ - 1). З другого боку, при градієнті швидкості, рівному 1, 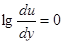 і коефіцієнт визначається по відрізку, що відсікається прямій на ординаті 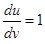. Чим вища в'язкість матеріалу, тим вище розташована його пряма на графіку.

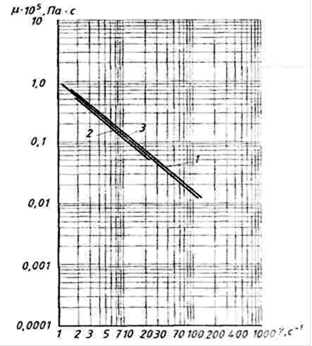
Мал.6.21. Крива реології глиномасси Галіцинського керамічного заводу: 1 - з урахуванням пружних і пластичних властивостей (конус); 2, 3 - з урахуванням тільки пластичних властивостей (2 - циліндр Ø0,062 м; 3 - циліндр Ø0,012 м).

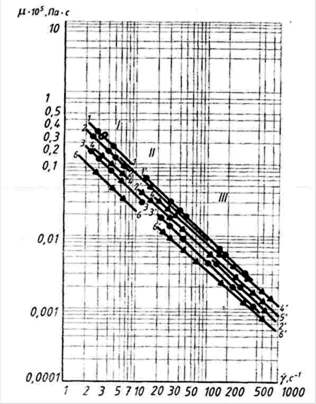
Мал.6.22. Графік залежності в'язкості від градієнта швидкості Беськудниковськой глиномасси вогкістю: 1-1' - 22%; 2-2' - 24%; 3-3' - 26%; 1-1' - 22% і Кембрійською глиномасси вогкістю: 4-4' - 20%; 5-5' - 24,5%; 6-6' - 26%; I - ділянка кривих, одержуваних на щілистій насадці шнекового преса; II - крива, одержувана на глинорозтирачі для Беськудниковськой глиномасси вогкістю 24%; III - ділянка кривих, одержуваних на лабораторній валковій установці.

Таким чином, шляхом порівняння кривої досліджуваної глини реології з кривою вивченою реології, можна на підставі графіка не тільки якісно оцінити деформативні властивості матеріалу, що цікавить нас, але, враховуючи однозначну залежність зусиль, що виникають у вузлах машин, від в'язкості матеріалу і їх геометричних характеристик, графічно визначити орієнтовну величину основних параметрів цих машин, що є початковими при їх подальших розрахунках.