Исходя из теоремы 8.1 и опираясь на характеризацию аффинных многообразий, представленную теоремой 4.8, мы докажем здесь следующую теорему:

Теорема 9.1. Пусть 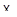, 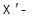аффинные пространства над телами 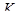, , 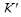отличными от поля 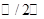; для того, чтобы отображение 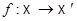было полуаффинным, достаточно, чтобы

1). Образ любой прямой в 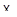 был прямой в 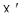, либо сводился к одной точке.

2). Аффинное подпространство в 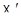, порожденное 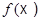, имело размерность .

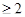       Мы подразделим доказательство этой теоремы на семь лемм; в каждой из них предполагается, что 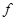 удовлетворяет условиям 1) и 2).

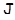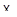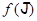Лемма 1. Если  есть ЛАМ в , то - ЛАМ в .

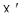Доказательство. Пусть 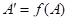 и 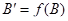- две различные точки в 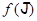. Тогда прямая  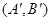есть по условию 1) образ прямой 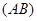; так как прямая 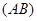содержится в 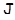, прямая  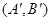содержится в 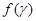. Результат теперь вытекает из теоремы 4.8.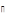

Лемма 2. Если 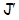- ЛАМ в  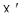и множество  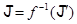непусто, то оно является ЛАМ в .

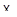Доказательство. Результат очевиден, если 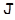 сводится к одной точке. В противном случае для любой пары различных точек 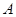,  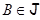прямая  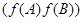содержится в  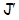согласно 1). Таким образом, прямая 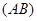содержится в  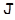и теорема 4.8 показывает, что  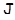есть ЛАМ.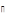

Лемма 3. Для любой непустой части 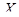 пространства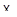

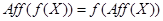.                        (1)

Доказательство. 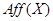 есть ЛАМ в 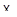, содержащее 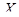; по лемме 1,  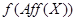есть ЛАМ в 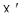, содержащее 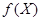. Отсюда следует включение

.

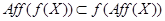Аналогично, по лемме 2, 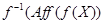есть ЛАМ в 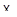, содержащее 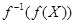, а потому и 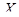; имеет место включение 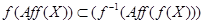; применение отображения  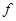дает .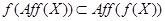

Окончательно получаем равенство (1).

Лемма 4. Пусть 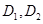- пара параллельных прямых в 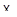. Если 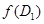сводится к точке, то же имеет место и для 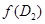. Если  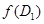- прямая, то и 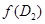- прямая, параллельная .

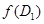Доказательство. Мы можем предположить, что 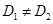. Тогда  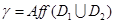есть ЛАМ размерности 2 в 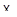, порожденное двумя точками 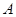, 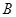одной из прямых и точкой  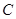другой прямой; по леммам 2и 3,  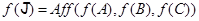есть ЛАМ размерности .

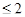А). Покажем сначала, чт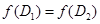о либо .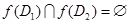

Допустим, что 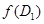 и 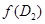 действительно имеют общую точку. Тогда найдутся точк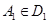и  и 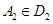, такие, что 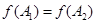. Выбирая  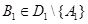и полагая по-прежнему 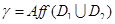, получим с помощью леммы 3, что

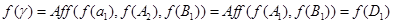
и аналогично

,

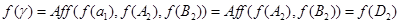откуда .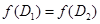

       Поскольку сформулированное утверждение при 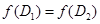очевидно, будем далее полагать 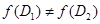, т.е. считать, что 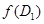и 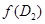 не имеют общих точек.

Б). Предположим, что 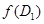- прямая в 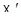и 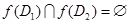; тогда  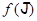имеет размерность 2.

       Если бы на прямой 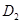существовали две точки 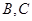, такие, что 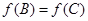, то для любой точки 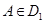мы имели бы 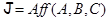и 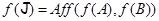, и тогда 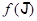не было бы двумерным вопреки предположению. Отсюда следует, что 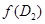- прямая.

       Значит, 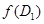и 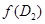 - две прямые без общих точек, лежащие в одном ЛАМ размерности 2, т.е. параллельные.

В). Если 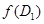 сводится к одной точке, то меняя ролям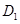и и 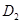и применяя результат Б), мы видим, что 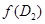также сводится к точке.

Лемма 5. Если 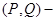пара точек в 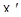, таких, что множества ,

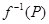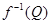
непусты, то 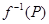 и 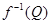- ЛАМ с общим направлением.

Доказательство. По лемме 2, 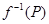 и 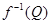 суть ЛАМ в 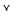. Предполагая, что 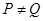, фиксируем точку 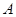в 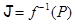и точку 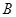в 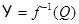; параллельный перенос на вектор  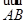обозначим через 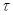. Для любой точки  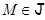прямая 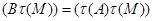параллельна прямой 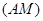, и поскольку образ прямой 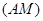сводится к одной точке 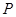, то образ прямой 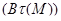сводится к одной точке 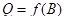. Таким образом, 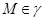влечет 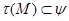и имеет место включение .

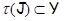 Меняя ролям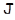и  и 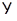, получим включение 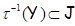, откуда 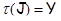. Итак, 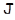,  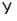имеют общее направление.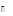

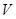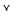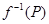Лемма 6. Обозначим через  общее направление непустых ЛАМ в  вида , где 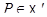, и пусть 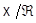- факторпространство  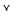по отношению эквивалентности 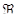, определенному условием .

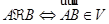 Тогда 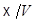имеет единственную аффинную структуру, такую, что каноническая проекция  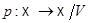является аффинной.

Доказательство. Выбор начала 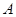 в 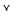 сводит дело к случаю факторпространства векторного пространства  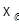По его векторному подпространству 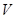, и оказывается, что достаточно применить теорему II.4.3, приняв точку  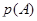за начало в .

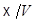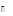
        Отметим, что 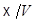является пространством орбит действия группы трансляций  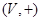на 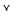; это есть множество ЛАМ с направлением 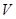.(см. §2).

       Лемма 7. В обозначениях леммы 6 отображение 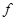представляется в ви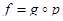де , где 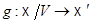- инъективное полуаффинное отображение; отсюда вытекает, что  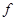полуаффинно.

Доказательство. Существование и инъективность 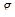 вытекают из того, что соотношение 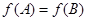равносильно 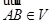(см. лемму 5), и тем самым 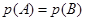. Для доказательства полуаффинности 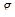покажем, что оно удовлетворяет условиям теоремы 8.1.

Пусть 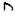– произвольная аффинная прямая 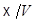, порожденная двумя различными элементами 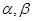из 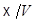. Без труда проверяется, что  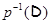есть ЛАМ в 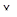, порожденное .

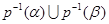       По лемме 3, 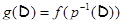есть ЛАМ, порожденное 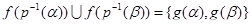; итак (в силу инъективности 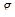), 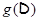является аффинной прямой .

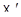Наконец, 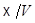не может сводиться к одной точке или прямо, так как тогда к точке или прямой сводилось бы и 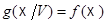, что противоречит условию 2). Поэтому .

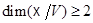       Отсюда следует, что 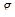удовлетворяет условиям 1) и 2), наложенным на 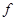, при условии замены 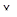на 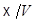. Лемма 4 показывает тогда, что образы при отображении 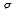двух параллельных прямых 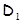,  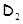из 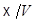- две параллельные прямые. Наконец, 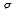удовлетворяет всем условиям теоремы 8.1 (после замены 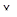на 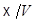). Следовательно,  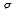полуаффинно и так же обстоит дело с .

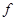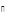
Теорема 9.1 тем самым полностью установлена.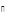

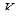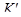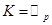Этот результат особенно интересен в случае, когда тела  и совпадают и не допускают других автоморфизмов, кроме тождественного (например, когда  или при 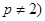: в этом случае мы получаем чисто геометрическую характеризацию аффинных отображений ранга  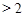пространства  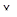в .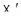

       Кроме того, очевидно, что теорема 9.1 потеряла бы силу при отсутствии условия 2): ведь любое отображение 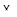на прямую тривиальным образом удовлетворяет условию 1).

       Так же и в случае 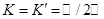 условие 1) выполнено для любого отображения  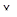в 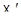(поскольку каждая прямая в  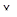и 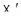состоит из двух точек). Теорема 9.1 теряет силу и в этом случае.

       Наконец, нельзя заменить требование «образ прямой есть прямая или точка» более слабым условием «образы коллинеарных точек коллинераны», даже при условии, что биективно.

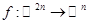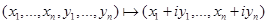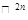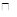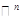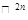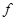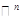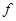       Например, ,  есть биекция векторного пространства над в векторное пространство над , и образ каждой прямой из при отображении содержится в фнекоторой прямой пространства , но не является полулинейным (поскольку  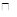и не изоморфны).

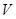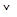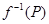Лемма 6. Обозначим через  общее направление непустых ЛАМ в  вида , где 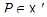, и пусть 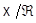- факторпространство  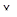по отношению эквивалентности 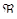, определенному условием .

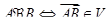 Тогда 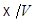имеет единственную аффинную структуру, такую, что каноническая проекция  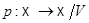является аффинной.

Доказательство. Выбор начала 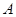 в 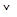 сводит дело к случаю факторпространства векторного пространства  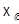По его векторному подпространству 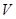, и оказывается, что достаточно применить теорему II.4.3, приняв точку  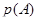за начало в .

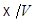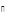
        Отметим, что 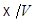является пространством орбит действия группы трансляций  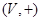на 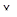; это есть множество ЛАМ с направлением 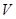.(см. §2).

       Лемма 7. В обозначениях леммы 6 отображение 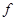представляется в ви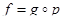де , где 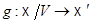- инъективное полуаффинное отображение; отсюда вытекает, что  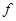полуаффинно.

Доказательство. Существование и инъективность 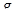 вытекают из того, что соотношение 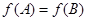равносильно 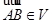(см. лемму 5), и тем самым 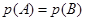. Для доказательства полуаффинности 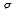покажем, что оно удовлетворяет условиям теоремы 8.1.

Пусть 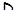– произвольная аффинная прямая 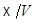, порожденная двумя различными элементами 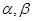из 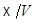. Без труда проверяется, что  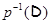есть ЛАМ в 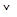, порожденное .

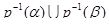       По лемме 3, 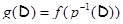есть ЛАМ, порожденное 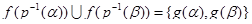; итак (в силу инъективности 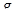), 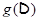является аффинной прямой .

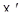Наконец, 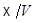не может сводиться к одной точке или прямо, так как тогда к точке или прямой сводилось бы и 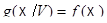, что противоречит условию 2). Поэтому .

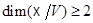       Отсюда следует, что 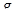удовлетворяет условиям 1) и 2), наложенным на 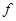, при условии замены 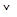на 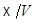. Лемма 4 показывает тогда, что образы при отображении 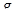двух параллельных прямых 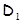,  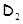из 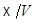- две параллельные прямые. Наконец, 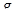удовлетворяет всем условиям теоремы 8.1 (после замены 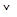на 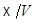). Следовательно,  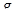полуаффинно и так же обстоит дело с .

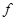Теорема 9.1 тем самым полностью установлена.

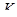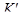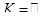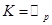Этот результат особенно интересен в случае, когда тела  и совпадают и не допускают других автоморфизмов, кроме тождественного (например, когда  или при 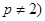: в этом случае мы получаем чисто геометрическую характеризацию аффинных отображений ранга  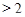пространства  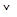в .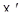

       Кроме того, очевидно, что теорема 9.1 потеряла бы силу при отсутствии условия 2): ведь любое отображение 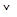на прямую тривиальным образом удовлетворяет условию 1).

       Так же и в случае 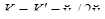 условие 1) выполнено для любого отображения  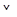в 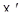(поскольку каждая прямая в  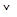и 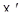состоит из двух точек). Теорема 9.1 теряет силу и в этом случае.

       Наконец, нельзя заменить требование «образ прямой есть прямая или точка» более слабым условием «образы коллинеарных точек коллинераны», даже при условии, что биективно.

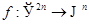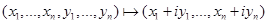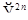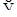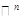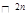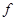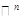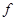       Например, ,  есть биекция векторного пространства над в векторное пространство над , и образ каждой прямой из при отображении содержится в некоторой прямой пространства , но не является полулинейным (поскольку  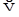и 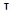не изоморфны).