Каждое векторное пространство 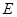 канонически снабжено аффинной структурой, так как  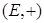действует на себе трансляциями; в этом случае нулевой вектор  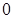называется также ”началом”  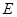и

    .

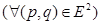
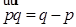ЛАМ пространства 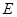, проходящие через 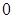, суть векторные подпространства в 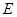; ЛАМ, проходящие через точку 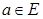, суть образы векторных подпространств  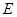при параллельном переносе .

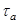Ради кратности ЛАМ, не проходящие через начало, будут называться собственно аффинными (поскольку они не являются ВПП в ).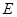

 Размерность линейного аффинного многообразия

Вернемся к случаю произвольного аффинного пространства ℰ; предшествующие рассмотрения позволяют определить размерность ЛАМ как размерность его направляющего ВПП. Отсюда появляются понятия: аффинной прямой (ЛАМ размерности 1) и аффинной плоскости (ЛАМ размерности 2). ЛАМ размерности 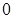 суть точки ℰ.

Аффинной гиперплоскостью называется ЛАМ, направляющее подпространство которого есть векторная гиперплоскость.

Пересечение линейных аффинных многообразий

Предложение 3. 3. Пусть 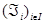- семейство аффинных подпространств в ℰ и  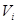для каждого 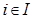- направляющее подпространство для .

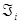Если пересечение 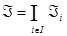 непусто, то оно является аффинным подпространством в  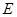с направляющим .

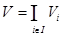Доказательство сразу получается из определения 3.1. При тех же обозначениях имеет место

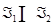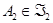Предложение 3.4. Для того, чтобы пересечение  двух ЛАМ в ℰ было непустым, необходимо и достаточно, чтобы существовали такие точки  и  , что 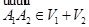, и тогда

.

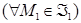
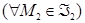
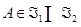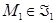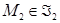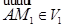Доказательство. Если , то для любых ,  имеем  и 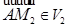. Таким образом, .

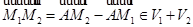Обратно, если существуют  и 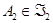, такие, что 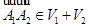, то можно представить  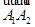в ви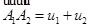де , где 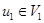, 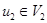. Тогда точка 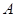, определяемая условием  , принадлежит 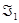 и, как легко видеть, 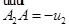. Это доказывает, что  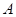принадлежит также 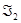, а тем самым  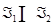не пусто.

Из предложения 3.4. можно получить примеры ЛАМ с пустым пересечением, а также

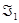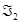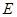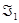Предложение 3.5. Если , - аффинные подпространства в ℰ, направляющие которых взаимно дополняют друг друга в , то  и 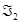 имеют единственную общую точку.

Параллелизм

Определение 3.3. Говорят, что два линейных аффинных многообразий 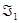,  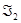вполне параллельны, если они имеют одно и то же направляющее подпространство: .

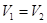Более общо, говорят, что 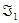 параллельно 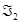, если направляющие пространства 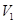,  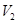 многообразий 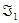,  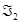удовлетворяют включению .

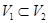Можно проверить, что отношение ” 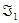 вполне параллельно (соответственно параллельно)  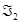” равносильно существованию трансляции  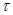пространства ℰ, такой, что  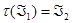(соответственно ).

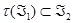Аффинное подпространство, порожденное подмножеством 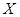пространства ℰ

Предположение 3.6. Если 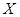- непустое подмножество в ℰ, то существует единственное аффинное подпространство в ℰ, обозначаемое 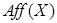, содержащее  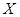и обладающее следующим свойством:

Любое аффинное подпространство ℰ , содержащее 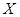, содержит и .

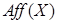Говорят, что 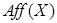 порождено .

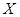Коротким способом доказательства предложения 3.6. является применение предложения 3.3.: 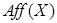 есть пересечение всех ЛАМ, содержащих 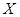. Недостаток этого рассуждения в том, что приходится привлекать семейство ”всех ЛАМ, содержащих 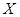”, о котором мало что известно и которое обычно даже несчетно!

Более элементарный и конструктивный способ состоит в выборе в 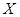 начальной точки 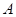, что сводит задачу к отысканию наименьшего векторного подпространства в ℰ _A, содержащего  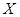(поскольку ЛАМ, содержащее 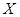, являются ВПП в ℰ). Таким образом,  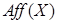есть ВПП в ℰ _A, порожденное 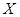; при этом сам характер задачи показывает, что это ВПП не зависит от выбора точки  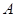в 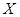. Если мы заметим, что направляющее подпространство для  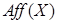есть ВПП в 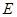, порожденное векторами 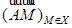, то получим также

Предложение 3.7. Пусть 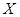- непустое подмножество в ℰ; для каждой точки  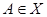положим 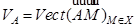. Тогда векторное пространство  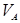не зависит от выбора  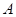и 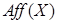 есть ЛАМ, проходящее через  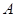с направлением .

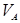Можно дать прямое доказательство этого утверждения, аналогичное доказательству предложения 3.2.

В частности, если 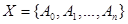- конечное множество, то векторное пространство  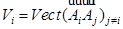не зависит от  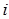и, следовательно, совпадает с

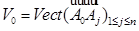 и .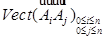

Отсюда вытекает

Предложение 3.8. Размерность аффинного подпространства, порожденного 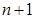 точками  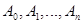пространства ℰ не превосходит 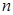; его размерность равна  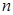тогда и только тогда, когда  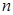векторов  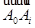( 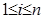) образуют свободное семейство.

Другие свойства ЛАМ изучаются в связи с понятием барицентра.