Следующая теорема оправдывает элементарное определение плоскости в школьном курсе геометрии как такого множества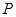 
точек, что каждая прямая, имеющая с ним две общие точки, вся принадлежит .
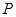Теорема 4.8. для того, чтобы непустая часть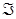 
пространства 
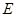была линейным аффинным многообразием, необходимо и достаточно, чтобы
a) если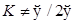 
- любая прямая, соединяющая две точки 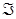, содержалась в 
;
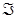b) если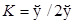 
- эвибарицентр любых трех точек 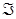лежал в .
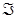Доказательство. Нам уже известна необходимость этого условия. Для доказательства достаточности выберем в 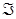точку 
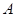и покажем, что 
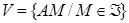есть ВПП пространства 
.
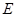a) Предположив, что 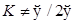, установим прежде всего, что условия 
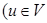и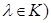 
влекут 
.
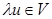Действительно, по предположению существует точка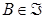 
, такая, что 
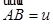. Точка 
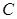, определенная условием 
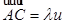, принадлежит прямой (АВ) и, значит, 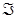, откуда следует, что .
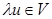Рассмотрим далее два любых вектора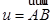 
и 
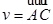в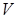 
и выберем 
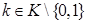(что возможно, так как 
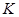не сводится к 
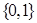). Точк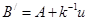и 
и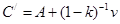 
(см. рис. 1) принадлежат соответственно прямым (АВ) и (АС), а поэтому и 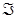. Следовательно, точка 
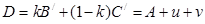принадлежит 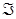, откуда 
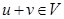. Итак 
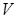есть ВПП в .
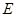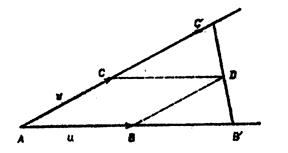
Рис. 1
b) Если 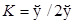, то тривиальным образом 
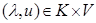влечет 
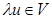(так как 
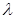может принимать только два значения 0, 1). Если 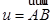, 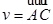- два вектора из 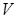, то точка 
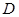, определяемая условием 
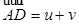, есть эквибарицентр 
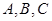, откуда и вытекает наше утверждение.
Аффинные и полуаффинные отображения
Определение 5.1. Пусть ℰ,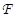 
- два аффинных пространства, ассоциированных соответственно с векторными пространствами 
, 
.
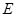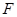Отображение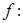 
ℰ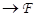 
называется полуаффинным (соответственно аффинным), если в ℰ существует такая точка 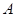, что отображение 
, 
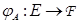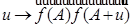полулинейно (соответственно линейно).
Предложение 5.1. Если в ℰ существует точка 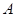, удовлетворяющая вышеуказанным требованиям, то им удовлетворяет любая точка ℰ и отображение 
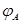не зависит от 
.
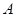Доказательство. Для любой пары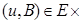 
ℰ имеем в силу линейности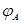 
,
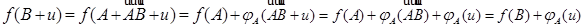что и доказывает требуемое.
Обозначения. Отображение 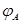обозначается 
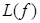и называется полулинейной (соответственно линейной) частью 
.
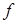Истолкование. Фиксируем в ℰ некоторую точку 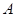и снабдим , 
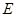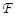векторными структурами, принимая за начало в ℰ точку 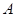, а в 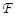- точку 
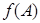. Тогда 
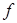будет полуаффинным (соответственно аффинным) в том и только том случае, если 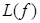- полулинейное (соответственно линейное) отображение ℰА в 
.
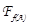В частности, изучение полуаффинных (соответственно аффинных) отображений пространства ℰ в себя, допускающих неподвижную точку 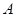, сводится к изучению полулинейных (соответственно линейных) отображений ℰ А в себя.
Так обстоит дело в случае геометрий, проектирований и симметрий (см. ниже).
Важно заметить, что полуаффинные (соответственно аффинные) отображения полностью определяется своей полулинейной (соответственно линейной) частью и образом одной точки.
Если 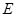, 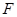- два векторных пространства, то полуаффинное (соответственно аффинное) отображение 
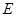и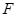 
есть отображение вида 
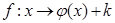, где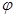 
полулинейно (соответственно линейно), а 
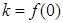- постоянный элемент.
Непосредственные следствия. Если 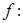ℰ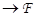 
полуаффинно, то
1) Образ ЛАМ в ℰ есть ЛАМ в .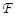
2) Прообраз ЛАМ в 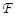есть ЛАМ в ℰ или пустое множество.
3) Для любой системы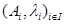 
взвешенных точек ℰ образ барицентра 
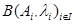есть барицентр 
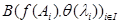, где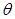 
обозначает изоморфизм тел, ассоциированных с 
.
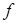Применение аффинных реперов
Теорема 5.2. Пусть ℰ, 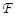- аффинные пространства над телами 
, 
, 
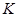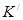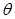- изоморфизм 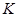на ,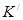 
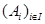- аффинный репер в ℰ и 
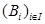- семейство точек 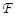, индексированное тем же множеством индексов 
.
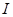Тогда существует единственное полуаффинное отображение 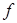пространства ℰ в 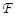, ассоциированное с изоморфизмом 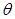, такое, что 
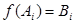для всех 
.
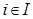Более того, 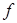биективно (соответственно инъективно, сюръективно) тогда и только тогда, когда семейство 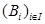есть аффинный репер (соответственно свободное семейство, семейство образующих) для .
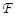Доказательство. Вернемся к теореме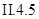 
, взяв одну из точек 
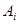в качестве начала в ℰ, а соответствующую точку 
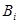- в 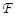; отображение 
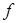определяется равенством
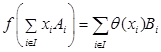
для любого конечного подмножества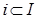 
и любой системы скаляров 
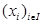, таких, что, 
.
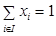В частности, аффинное отображение ℰ в 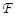определяется заданием образа аффинного репера из ℰ.
Приложение: уравнение аффинной гиперплоскости или ЛАМ
Опираясь на исследование, проведенное в параграфе II.6, легко получаем
Предложение 5.3. Пусть ℰ- аффинное пространство над телом 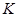. Тогда
a) Если 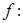ℰ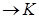 
- непостоянное аффинное отображение, то 
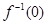- аффинная гиперплоскость в ℰ с направлением 
.
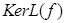b) Обратно, если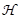 
- аффинная гиперплоскость в ℰ, то существует аффинное отображение 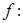ℰ 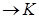, такое, что 
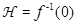, и все аффинные отображения ℰ в 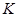с этим свойством суть отображения 
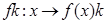, где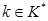 
.
Если ℰ- аффинное пространство конечной размерности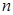 
, то каждое ЛАМ размерности 
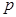в ℰ определяется системой уравнений вида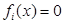 
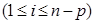, где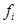 
- аффинные отображения ℰ в 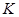, линейные части которых независимы.
Характеризация аффинных отображений
Теорема 5.4. Пусть ℰ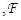 
- два аффинных пространства над одним и тем же телом 
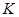. Для того, чтобы отображение 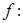ℰ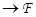 
было аффинным, необходимо и достаточно, чтобы
a) при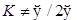 
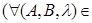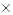ℰ 
ℰ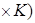 
;
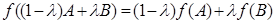b) при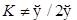 
образ эквибарицентра любых трех точек ℰ был эквибарицентром их образов.
Доказательство (аналогичное случаю теоремы 4.8.).
a) При фиксированной точке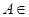 
ℰ соотношение a) показывает, что для любого вектора 
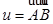направляющего пространства 
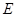имеем
.
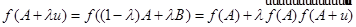Отображение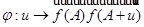 
удовлетворяет, следовательно, условию 
.
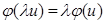Чтобы доказать, что выполняется и условие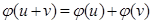 
для любых 
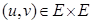, выберем такие 
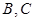, что 
, 
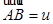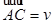и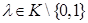 
, определим точки 
, 
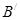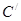условиями 
, 
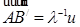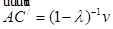. Применяя условие a), получим тогда 
,
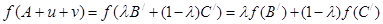откуда
.
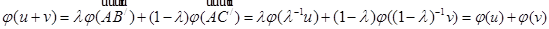Можно также сформулировать теорему 5.4. так: отображение ℰ в 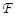является аффинным тогда и только тогда, когда его ограничение на любую аффинную прямую в ℰ аффинно.
В дальнейшем мы дадим чисто геометрическую характеристику полуаффинных отображений.
Дата: 2019-05-29, просмотров: 259.
