Векторная интерпретация барицентров.

Вернемся к обозначениям §6. Инъекция 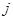позволяет нам отождествить  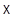с аффинной гиперплоскостью  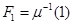в , в 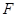то время как ее линейная часть  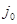позволяет отождествить 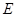с векторной гиперплоскостью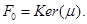

Предложение 7.1. Пусть 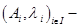конченое семейство взвешенных точек 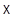, где точки 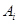отождествлены с элементами 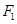. Для того, чтобы элемент 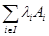из 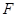принадлежал 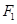(соотв. 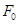), необходимо и достаточно, чтобы 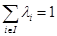(соотв. ).

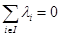Доказательство. Это вытекает из соотношения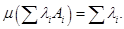

Правило. Отождествление 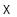 с подмножеством в 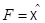позволяет без предосторожностей записывать любые конечные линейные комбинации  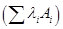элементов 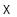. Но такая комбинация представляет элемент из 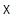только тогда, когда 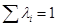( этот элемент будет барицентром системы 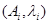); если же 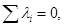то 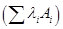представляет элемент из 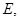равный 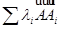для любой точки .

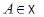Приложения. 1). Для того, чтобы три точки 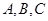 из 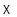 были коллинеарны, необходимо и достаточно, чтобы существовали не равные одновременно нулю скаляры  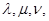такие, что

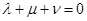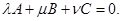                и                                         (1)

Соотношения (1) на самом деле равносильны одному соотношению 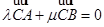; они интересны своей симметричной формой относительно  и возможностью складывать подобные соотношения.

2). Если 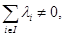 то барицентром системы  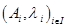является точка пересечения с  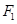векторной прямой с направляющей  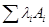в .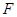

3). Для того чтобы семейство 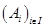 точек из  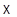было аффинно свободным (соотв. аффинно порождающим), необходимо и достаточно, чтобы семейство  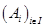было свободным (соотв. семейством образующих) в векторном пространстве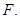

В частности, аффинный репер 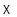 является базисом 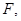содержащимся в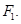

Векторная интерпретация аффинных отображений.

Мы начнем с установления одного общего результата, независимого от теории векторных продолжений

Предложение 7.2. Пусть 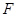, 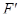- два векторных пространства над одним и тем же телом 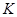и 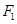 (соответственно 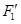) – аффинная гиперплоскость в 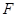(соотв. 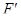), не проходящая через начало; обозначим 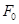(соответственно 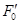) векторную гиперплоскость, параллельную  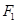(соответственно ).

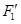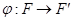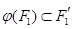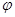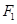А) Если  - линейное отображение, такое, что , то ограничение  на  есть аффинное отображение  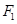в 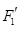, линейная часть которого есть ограничение  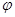на .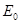

Б) обратно, если 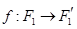 - аффинное отображение, то существует единственное линейное отображение 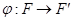, ограничения которого на  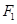совпадает с .

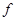Доказательство.

А) Если 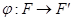 линейно и 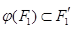, то для любых точек 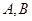из 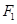 имеем и 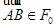. Ограничения  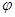на 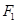 аффинно с линейной частью , .

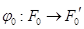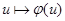Б) Обратно, пусть 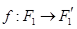- аффинное отображение. Фиксируем точку  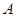в 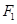 и обозначим через  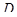(соответственно 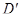) векторную прямую в 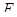(соответственно 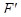), порожденную  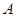(соответственно 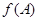) (рис 4). Тогда 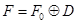, , 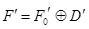и искомое линейное отображение должно удовлетворять следующим двум условиям:

1. ,

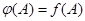2. Ограничения 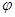 на 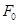 равно линейной части .

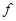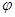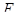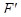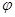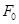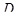Но существует единственное линейное отображение  из  в , удовлетворяющее этим условиям (  определено своими ограничениями на дополнительные ВПП  и  пространства 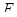); тогда ограничение  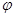на 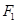 - есть аффинное отображение с той же линейной частью, что и 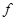, и принимающее в  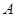то же значение, что и 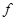, а тем самым равное 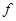, откуда вытекает доказываемый результат.

Существует, следовательно, биективное соответствие между аффинными отображениями 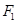 в 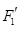 и линейными отображениями  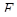в 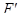, удовлетворяющими условию .

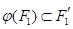С другой стороны, есл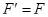и , и 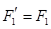, это соответствие сохраняет композицию отображений (композиция ограничений двух отображений совпадает с ограничением их композиции).

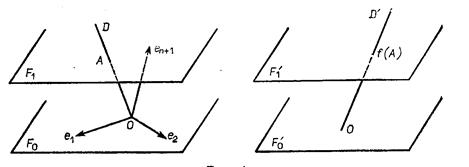
                                       Рис.4

Наконец, если 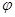 - автоморфизм  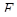и 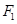 - аффинная гиперплоскость в 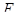, то включение  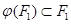влечет равенства 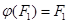. В самом деле,  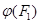есть аффинная гиперплоскость в 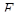, и достаточно применить следствие теоремы II 6.2, вернувшись к векторному случаю путем замены начала в .

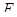       Т.о. мы можем сформулировать

Предложение 7.3. Пусть 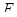 - векторное пространство,  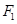- аффинная гиперплоскость в 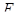, не проходящая через начало. Существует изоморфизм группы аффинных биекций  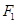на стабилизаторе  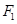в 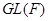 (подгруппу 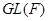, состоящую из изоморфизмов 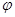, для которых ).

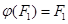       Эти результаты применимы, в частности, к случаю, когда, 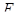,  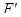- векторные продолжения аффинных пространств 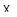, , 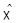а 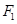,  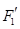- образы 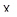,  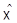при канонических погружениях 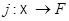, 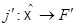: всякое аффинное отображение  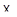в 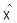, отождествляется с линейным отображением  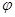пространства 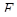в пространство 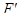, удовлетворяющим требованию 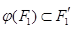, и группа аффинных биекций  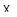отождествляется с подгруппой 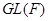, сохраняющей аффинную гиперплосклость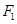

       Случай конечной размерности.

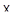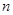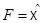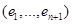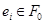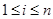Если аффинное пространство  имеет конечную размерность , то в  можно выбрать базис  так, что  при  и 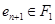. Тогда  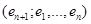есть декартов репер в  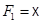с началом  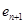(рис 4).

       В этом случае 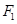 является множеством точек 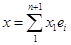пространства 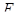, таких, что 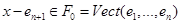; следовательно, это аффинная гиперплоскость с уравнением  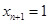в базисе 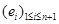. Эндоморфизмы  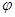пространства 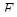, удовлетворяющие условию 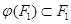, - это те эндоморфизмы, матрица которых в базисе 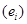имеет вид

,                            (2)

где 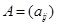 - квадратная матрица порядка 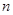. Эндоморфизму  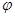с матрицей (2) соответствует аффинное отображение 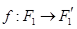, координатное выражение которого в декартовом репере  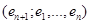имеет форму

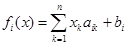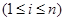 ,                (3)

Матричные вычисления показали бы, что для этого соответствия соблюдаются правила композиции отображений. С другой стороны, эндоморфизм 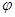 с матрицей (2) обратим тогда и только тогда, когда обратима матрица (2), и тогда выполняется и равенство 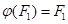. Таким образом, получается

Теорема 7.4. Группа аффинных биекций 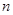-мерного аффинного пространства изоморфна подгруппе линейной группы 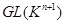, образованной матрицами вида (2), где  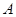принадлежит .

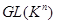В частности, группа аффинных биекций 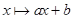 тела 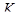 изоморфна подгруппе в 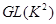, состоящей из матриц вида .

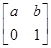8.Геометрическая характеризация инъективных полуаффинных отображений.

       Ниже мы обозначаем через 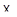,  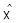два аффинных пространства, ассоциированных соответственно с векторными пространствами  над произвольными телами 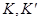. Мы дадим чисто геометрическую характеризацию полуаффинных отображений  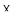в 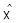. Для ясности начнем со случая инъективных отображений.

       Теорема 8.1. Допустим, что 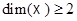. Для того, чтобы инъективное отображение  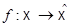было полуаффинным, необходимо и достаточно, чтобы оно удовлетворяло следующим двум условиям:

1. Образ любой аффинной прямой из 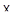 был аффинной прямой в ;

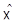2.  Образы двух параллельных прямых был параллельными прямыми.

Доказательство. Необходимость условия очевидна. Доказательство

достаточности проведем в несколько этапов, все время предполагая, что 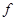 удовлетворяет условиям 1) и 2).

А). Образы при 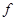 двух различных прямых 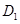,  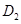из 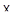 суть также две различные прямые.

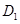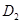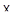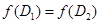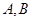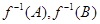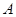В самом деле, пусть ,  - прямые в , имеющие один и тот же образ , пусть  - две различные точки их общего образа. Тогда прообразы  точек  и 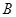принадлежат  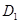и 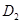 одновременно и различны (в силу иньективности 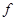), откуда следует, что .

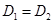Б). Отображение 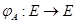,  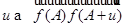не зависит от выбора 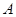в .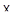

В самом деле, пусть другая точка 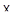 и 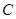,  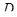таковы, что 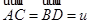. Если

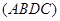- несплющенный параллелограмм, то из 2) и А) следует, что его образ 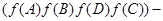тоже настоящий параллелограмм, откуда

,

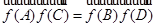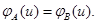
Если точки 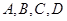 принадлежат одной прямой 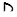, то предположение  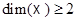позволяет выбрать в 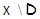точки 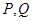 так, что 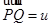. Применяя предыдущий случай, имеем

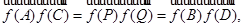
откуда .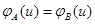

Отображение 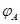 обозначаем отныне просто .

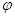В). Отображение 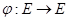 инъективно и удовлетворяет условию

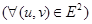
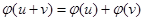.             (1)

Инъективность 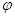 сразу следует из инъективности 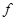. С другой стороны, для любых данных  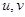выберем в  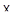такие точк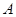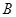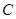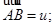и , , ,  и 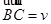. Тогда .

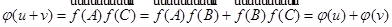Д). Существует отображение 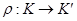, такое, что

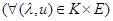
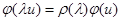.                (2)

Доказательство. Достаточно найти 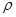, удовлетворяющее условию (2) при 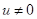. Для заданной пары  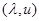выберем , ,  в 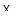 так, что 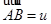, 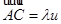. Так как точк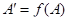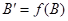и ,  и 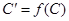 коллинеарны, то коллинеарны и векторы 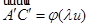; отсюда вытекает существование некоторого скаляра, скажем 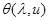, такого, что 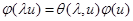. Остается доказать, что  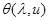не зависит от вектора  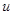(по предположению ненулевого).

1). Если 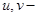два неколлинеарных вектора, то неколлинеарны и 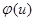, 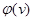; в противном случае образы двух прямых 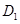, , 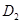проходящих через одну и ту же точку  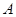с направляющими 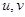, совпадали бы, что невозможно в силу А).

Для любого 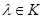имеем

,

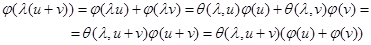откуда в силу неколлинеарности ,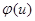  

.

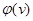
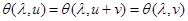2). Если 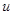, 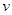- коллинеарные ненулевые векторы, то предположение  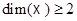позволяет выбрать  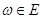 так, что пары  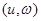и 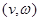 свободны. Отсюда находим, что

.

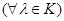
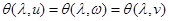Так для каждого 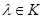 отображение 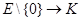,  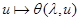есть константа, мы обозначим ее через .

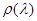Е). Отображение 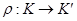 является изоморфизмом тел.

 Выбрав 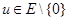, мы увидим прежде всего, что соотношения  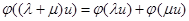и 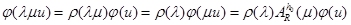 влекут (с учетом )

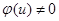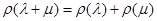 и ,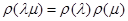

т.е. показывают, что 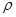 - гомоморфизм тел.

       Наконец, для любой точки 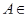 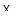отображение  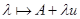есть биекция  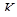на прямую 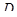; ограничение  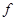на 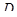есть биекция 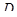на прямую 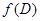. Следовательно, композиция 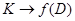, 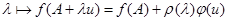биективна. Отсюда вытекает, что отображение  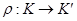биективно.

       Итак, 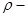изоморфизм тел, 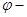полулинейное отображение, ассоциированное с 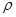, и 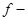полуаффинное отображение.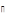

Случай плоскости.

Есл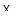и и 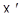 двумерны, то условие 2) в теореме 8.1 следует из условия 1) и инъективности 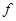. Мы можем, таким образом, сформулировать

Следствие. Если 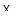, 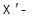аффинные плоскости и 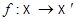- инъективное отображение, такое, что образ любой прямой в 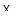есть прямая в 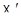, то 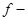полуаффинное отображение.

Замечание. Условия теоремы 8.1 выполняются, в частности, если 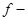инъективное отображение 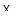в себя, такое, что образ любой прямой  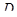есть прямая, параллельная 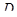; тогда можно непосредственно доказать, что  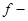дилатация.