Теорема 5.5. Если 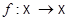 - полуаффинное отображение и множество
- полуаффинное отображение и множество 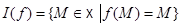 его неподвижных точек не пусто, то оно является ЛАМ с направляющим множеством
его неподвижных точек не пусто, то оно является ЛАМ с направляющим множеством 
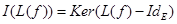 , состоящим из неподвижных элементов отображения
, состоящим из неподвижных элементов отображения 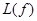 .
.
С другой стороны, если 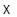 конечномерно и
конечномерно и 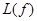 не имеет других неподвижных элементов, кроме 0, то
не имеет других неподвижных элементов, кроме 0, то 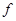 имеет единственную неподвижную точку.
имеет единственную неподвижную точку. 
Доказательство. Если фиксировать точку 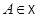 , условие
, условие 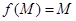 равносильно
равносильно  и, значит, условию
и, значит, условию  где
где 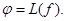
· Если 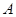 - неподвижная точка
- неподвижная точка 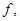 то
то 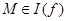 равносильно
равносильно 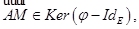 откуда вытекает первое утверждение.
откуда вытекает первое утверждение.
· Если 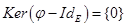 , то отображение
, то отображение 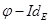 инъективно и потому в случае конечной размерности
инъективно и потому в случае конечной размерности 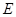 биективно; в
биективно; в 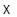 существует единственная точка
существует единственная точка 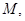 такая, что
такая, что 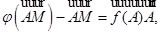 откуда следует второе утверждение.
откуда следует второе утверждение. 
Важное замечание. Если 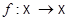 - произвольное отображение и
- произвольное отображение и  - биекция, то
- биекция, то 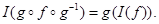
Это общее замечание особенно полезно в случае аффинных отображений.
Аффинные и полуаффинные группы.
Если  и
и 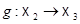 - два аффинных (соотв. полуаффинных) отображения, то
- два аффинных (соотв. полуаффинных) отображения, то 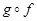 также есть аффинное (соотв. полуаффинное) отображение и
также есть аффинное (соотв. полуаффинное) отображение и 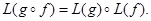 Отсюда выводится
Отсюда выводится
Теорема 5.6. Пусть 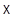 - аффинное пространство, ассоциированное с векторным пространством
- аффинное пространство, ассоциированное с векторным пространством 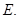 Аффинные (соотв. полуаффинные) биекции
Аффинные (соотв. полуаффинные) биекции 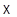 на
на 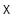 образуют группу, которую мы обозначаем
образуют группу, которую мы обозначаем 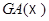 (соотв.
(соотв. 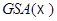 ). Отображение
). Отображение 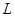 (линейная или полулинейная часть) есть гомоморфизм
(линейная или полулинейная часть) есть гомоморфизм 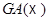 на
на 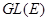 и
и  на группу
на группу  полулинейных биекций
полулинейных биекций 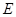 на
на 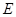 .
.
Наконец, для любой точки  в
в 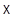 ограничение
ограничение 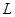 на группу изотропии точки
на группу изотропии точки 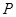 в
в 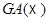 (соотв.
(соотв. 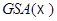 ) является изоморфизмом этой группы на
) является изоморфизмом этой группы на 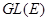 (соотв.
(соотв.  ).
).
Последнее утверждение получим, выбирая  в качестве начала в
в качестве начала в 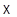 .
.
Следствие. Если 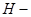 подгруппа в
подгруппа в 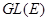 (соотв. в
(соотв. в 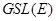 ), то
), то 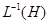 есть подгруппа в
есть подгруппа в 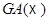 (соотв. в
(соотв. в 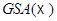 ); при этом если
); при этом если  инвариантная подгруппа, то такова же и
инвариантная подгруппа, то такова же и 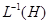 .
.
В частности, если 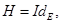 то
то 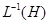 есть инвариантная подгруппа в
есть инвариантная подгруппа в 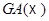 , образованная трансляциями.
, образованная трансляциями.
Если 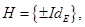 то
то 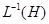 есть инвариантная подгруппа в
есть инвариантная подгруппа в 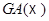 , образованная трансляциям и центральными симметриями.
, образованная трансляциям и центральными симметриями.
Если 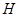
 инвариантная подгруппа группы
инвариантная подгруппа группы 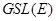 , образованная векторными гомотетиями, то
, образованная векторными гомотетиями, то 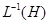 есть инвариантная подгруппа в
есть инвариантная подгруппа в  , называемая группой дилатаций.
, называемая группой дилатаций.
Пусть 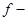 дилатация, не сводящаяся к трансляции; тогда
дилатация, не сводящаяся к трансляции; тогда  векторная гомотетия вида
векторная гомотетия вида 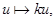 где
где 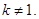 В этом случае
В этом случае 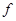 имеет единственную неподвижную точку
имеет единственную неподвижную точку 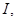 определяемую из условия
определяемую из условия 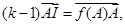 где
где 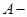 произвольная точка
произвольная точка 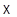 . Таким образом,
. Таким образом, 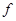 выражается как
выражается как 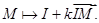 Такое отображение называется гомотетией с центром
Такое отображение называется гомотетией с центром 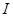 и коэффициентом
и коэффициентом 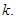
Сформулируем
Предложение 5.7. Трансляции и гомотетии 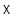 составляют инвариантную подгруппу группы
составляют инвариантную подгруппу группы 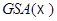 , называемую группой дилатаций
, называемую группой дилатаций 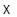 . Мы обозначаем ее
. Мы обозначаем ее 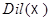 .
.
Если основное тело 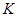 коммутативно, то группа
коммутативно, то группа 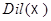 является инвариантной подгруппой группы
является инвариантной подгруппой группы 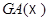 .
.
Проектирования
Назовем проектированием 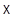 любое аффинное отображение
любое аффинное отображение 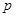 пространства
пространства 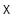 в себя, удовлетворяющее условию
в себя, удовлетворяющее условию 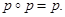

Рис. 2
Для такого отображения любая точка 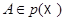 является неподвижной; принимая такую точку за начало, мы приходим к случаю проектирования для векторного пространства
является неподвижной; принимая такую точку за начало, мы приходим к случаю проектирования для векторного пространства 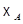 . Отсюда вытекает существование таких отображений, а также следующая их геометрическая характеризация:
. Отсюда вытекает существование таких отображений, а также следующая их геометрическая характеризация:
Предложение 5.8. Отображение 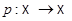 является проектированием, если существует ВПП
является проектированием, если существует ВПП 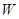 пространства
пространства 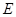 и ЛАМ
и ЛАМ 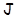 в
в 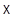 с направляющим подпространством
с направляющим подпространством 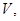 дополнительным к
дополнительным к 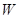 , такие, что для любой точки
, такие, что для любой точки 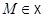 ее образ
ее образ  есть точка пересечения
есть точка пересечения  с ЛАМ, проходящим через
с ЛАМ, проходящим через 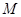 с направлением
с направлением 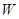 (рис. 2).
(рис. 2).
Аффинные симметрии
Теорема 5.9. Пусть 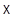 - аффинное пространство, ассоциированное с векторным пространством
- аффинное пространство, ассоциированное с векторным пространством 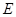 над телом
над телом 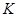 характеристики
характеристики 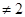 .
.
Для того, чтобы аффинное отображение 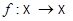 было инволютивным, необходимо и достаточно, чтобы оно имело по меньшей мере одну неподвижную точку и чтобы его линейная часть была векторной симметрией
было инволютивным, необходимо и достаточно, чтобы оно имело по меньшей мере одну неподвижную точку и чтобы его линейная часть была векторной симметрией 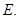
Такое отображение называется аффинной симметрией.
Доказательство. Если 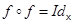 и
и 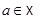 , то образом середины отрезка
, то образом середины отрезка 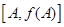 будет середина отрезка
будет середина отрезка 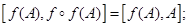 таким образом, эта точка инвариантна при отображении
таким образом, эта точка инвариантна при отображении 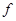 и, выбрав ее за начало, мы сведем дело к векторному случаю.
и, выбрав ее за начало, мы сведем дело к векторному случаю. 
Предложение 5.10. Отображение 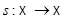 является аффинной симметрией, если существуют ВПП
является аффинной симметрией, если существуют ВПП 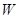 пространства
пространства 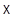 и ЛАМ
и ЛАМ  с направлением, дополнительным к
с направлением, дополнительным к  такие, что для любой точки
такие, что для любой точки 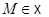 (см.рис.2)
(см.рис.2)
1). 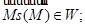
2). Середина 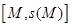 принадлежит
принадлежит 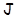 .
.
Если  сводится к одной точке
сводится к одной точке 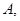 то
то 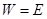 и
и 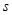 есть центральная симметрия с центром
есть центральная симметрия с центром 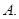
Теорема Фалеса
Пусть по-прежнему 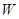 есть ВПП в
есть ВПП в 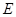 и
и 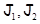 - два аффинных пространства в
- два аффинных пространства в 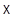 , направляющие которых соответственно
, направляющие которых соответственно 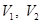 дополнительны к
дополнительны к 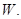 Обозначим через
Обозначим через  (соотв.
(соотв.  ) ограничение проектирования
) ограничение проектирования 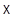 на
на 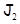 (соотв.
(соотв.  ) параллельно
) параллельно 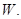 Тогда, как легко видеть,
Тогда, как легко видеть,  является аффинной биекцией
является аффинной биекцией 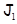 на
на 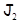 , обратная к которой есть
, обратная к которой есть 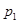 . Образ
. Образ 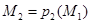 точки
точки 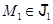 определяется условиями
определяется условиями 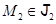 и
и 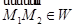 (см. рис. 3).
(см. рис. 3).
В более общей форме теорема Фалеса есть не что иное, как констатация того факта, что установленное
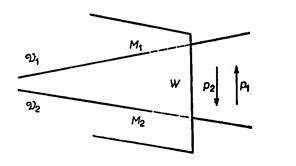
Рис.3
указанным способом соответствие между 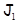 и
и 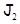 является аффинным.
является аффинным.
В частности, если 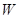
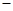 векторная гиперплоскость, то справедлива
векторная гиперплоскость, то справедлива
Теорема 5.11. Аффинные гиперплоскости, параллельные некоторой фиксированной гиперплоскости, высекают на произвольной паре не параллельных им прямых пропорциональные отрезки.
§6. Каноническое погружение аффинного пространства в векторное. Приложения.
Пусть снова 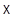 - аффинное пространство, ассоциированное с векторным пространством
- аффинное пространство, ассоциированное с векторным пространством 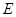 . Как мы уже видели, выбор начала в
. Как мы уже видели, выбор начала в 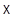 позволяет отождествить
позволяет отождествить 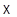 с
с  теперь мы докажем, что
теперь мы докажем, что 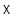 канонически отождествляется с аффинной гиперплоскостью некоторого пространства
канонически отождествляется с аффинной гиперплоскостью некоторого пространства 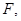 изоморфного
изоморфного 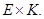
Метод будет состоять в сопоставлении каждой точке 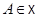 отображения
отображения 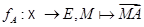
Предварительно сформулируем такое утверждение:
Лемма. Пусть 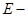 левое векторное пространство над телом
левое векторное пространство над телом 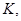 а
а 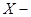 произвольное множество. Тогда множество
произвольное множество. Тогда множество 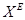 отображений
отображений 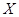 в
в 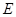 есть левое векторное пространство над
есть левое векторное пространство над 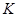 по отношению к обычным операциям сложения функций и умножению их слева на скаляры:
по отношению к обычным операциям сложения функций и умножению их слева на скаляры:
 и
и 
В силу доказанного искомое векторное пространство 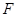 будет ВПП в
будет ВПП в 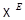 , порожденным отображениями
, порожденным отображениями 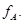 Поэтому мы начнем с изучения этого пространства
Поэтому мы начнем с изучения этого пространства 
Предложение 6.1. Пусть 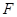 - векторное подпространство в
- векторное подпространство в 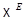 , порожденное функциями
, порожденное функциями 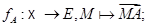 пуст, далее,
пуст, далее, 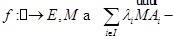 элемент из
элемент из 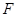 . Тогда
. Тогда
А). Сумма  зависит только от функции
зависит только от функции 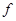 и притом линейно, т.е. является линейным отображением
и притом линейно, т.е. является линейным отображением 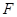 в
в 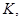 которое мы обозначим
которое мы обозначим 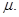
Б). Если 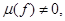 то существует единственная точка
то существует единственная точка 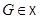 , такая, что
, такая, что 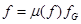 .
.
В). Если 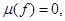 то
то 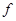 постоянна.
постоянна.
Доказательство. Заметим сначала, что утверждение А) не очевидно, так как могут существовать различные системы взвешенных точек 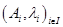 , такие, что
, такие, что 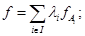 но оно легко вытекает из того факта, что для любой пары
но оно легко вытекает из того факта, что для любой пары 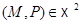 выполнено соотношение
выполнено соотношение
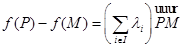 , (1)
, (1)
которое доказывает существование и линейность функции 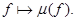
Б). Если 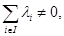 выберем в
выберем в 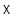 произвольную точку
произвольную точку  Соотношение (1) показывает, что в
Соотношение (1) показывает, что в 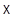 существует единственная точка
существует единственная точка  такая, что
такая, что  она определяется условием
она определяется условием 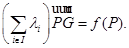 Из (1) также видно, что эта точка – единственная, для которой
Из (1) также видно, что эта точка – единственная, для которой 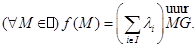 Таким образом, барицентр семейства
Таким образом, барицентр семейства 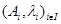 зависит только от функции
зависит только от функции 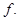
В). Наконец, последнее утверждение также вытекает из (1). 
Следствие. 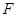 является теоретико-множественным объединением векторного пространства постоянных функций и множества функций вида
является теоретико-множественным объединением векторного пространства постоянных функций и множества функций вида 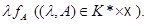
Предложение 6.2. Пусть 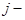 отображение
отображение 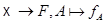 и пусть
и пусть 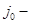 отображение
отображение 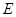 в
в 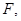 которое любому вектору
которое любому вектору  ставит в соответствие постоянную функцию, равную
ставит в соответствие постоянную функцию, равную 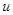 на
на 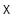 .
.
Тогда 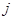 аффинно с линейной частью
аффинно с линейной частью 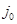 и потому инъективно; при этом
и потому инъективно; при этом 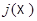 есть аффинная гиперплоскость
есть аффинная гиперплоскость 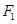 в
в 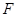 с уравнением
с уравнением 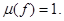
Доказательство. Для любой пары  разность
разность  есть постоянная функция
есть постоянная функция 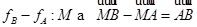 ; положим
; положим  . Таким образом,
. Таким образом, 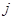 аффинно,
аффинно, 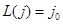 и
и 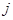 инъективно, как и
инъективно, как и 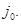
С другой стороны, как показывает предыдущее предложение, функции 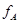 суть элементы
суть элементы 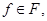 удовлетворяющие условию
удовлетворяющие условию 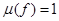 .
. 
Теорема 6.3. К каждому аффинному пространству 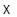 , ассоциированному с векторным
, ассоциированному с векторным  -пространством
-пространством 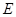 , можно канонически присоединить:
, можно канонически присоединить:
· Векторное пространство  изоморфное
изоморфное 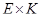 ,
,
· Ненулевую линейную форму 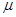 на
на 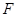 ,
,
· Аффинную инъекцию 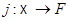 , такую, что
, такую, что 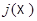 - аффинная гиперплоскость в
- аффинная гиперплоскость в 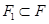 с уравнением
с уравнением 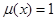
Доказательство . Остается только установить изоморфизм между 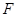 и
и 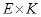 . Для этого достаточно заметить, что какова бы ни была точка
. Для этого достаточно заметить, что какова бы ни была точка 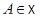 , отображение
, отображение  ,
, 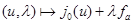 линейно и биективно. Установленный таким путем изоморфизм очевидным образом зависит от выбора точки
линейно и биективно. Установленный таким путем изоморфизм очевидным образом зависит от выбора точки 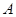 .
.
Заметим, что аффинная гиперплоскость  имеет в качестве направляющей векторную гиперплоскость
имеет в качестве направляющей векторную гиперплоскость 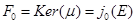 постоянных функций, которая отождествляется с
постоянных функций, которая отождествляется с 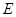 .
.
Замечания. 1). Векторную структуру на множестве  можно определить непосредственно, не прибегая к векторному пространству
можно определить непосредственно, не прибегая к векторному пространству 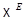 , но это связано с утомительными выкладками.
, но это связано с утомительными выкладками.
2). Особый интерес теоремы 6.3 в том, что она обеспечивает каноническое погружение 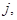 единственным образом определяемое заданием
единственным образом определяемое заданием 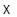 .
.
Обозначения. Векторное пространство 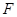 , построенное таким образом, называется векторным продолжением
, построенное таким образом, называется векторным продолжением 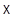 и обозначается
и обозначается 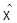 .
.
Если 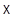 имеет размерность
имеет размерность  то размерность
то размерность  равна
равна  . Мы увидим, что введение этого пространства позволяет прояснить многие вопросы.
. Мы увидим, что введение этого пространства позволяет прояснить многие вопросы.
Дата: 2019-05-29, просмотров: 353.