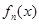
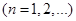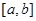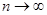Теорема 1. Нехай функції  неперервні на проміжку  і при  рівномірно прямують до граничної функції  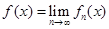[очевидно, також неперервній], a  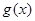— функція з обмеженою зміною. Тоді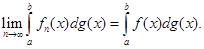

Доведення. По заданому 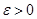 знайдеться таке 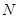, що при  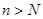буде для всіх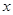  

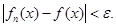
Тоді, в силу 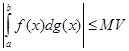для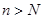

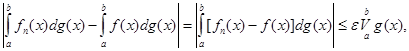
що, враховуючи довільність 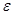, і доводить теорему.

Теорема 2. Нехай тепер функція 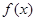 неперервна а проміжку 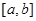, а функції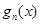 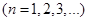 — всі з обмеженою зміною на цьому проміжку. Якщо повні зміни цих функцій в їх сукупності обмежені:

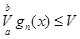
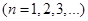
і 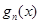 при 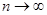 прямують до граничної функції

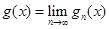, то

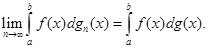
Доведення. Перш за все впевнимося у тому, що гранична функція 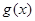 сама також буде мати обмежену зміну. Розкладемо проміжок  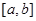довільним чином на частини точками 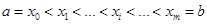, будемо мати (при будь-якому )

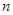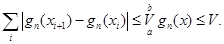
Переходячи границі тут при 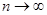, отримаємо  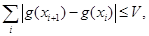звідки і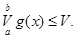

Складемо суми Стілтьєса ,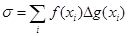

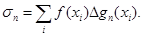
Якщо припустити, що проміжок 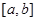 при цьому розкладений на такі маленькі частини, що коливання функції  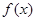у кожній з них буде вже менше довільного наперед взятого числа 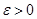, то, при всіх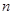  

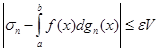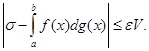,       (27)

З іншого боку, якщо розбиття, обране під вказаною умовою фіксувати, то очевидно 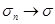 а при 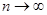, так що знайдеться таке 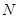, що для  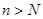буде

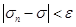.                (27)

Тоді для тих самих значень 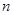 будемо мати, в силу (27) і (28),

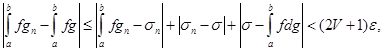
звідки, враховуючи довільність 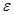, і випливає необхідний висновок. [1;7]

Висновки

У даній роботі розглянуто означення і основні властивості інтеграла Стілтьєса, його зв’язок, особливості і відмінності від інших визначених інтегралів.

В ході виконання курсової роботи були з’ясовані загальні умови існування інтегралу Стілтьєса та 3 класи випадків його існування, а також вивчено порядок зведення інтегралу Стілтьєса до інтегралу Рімана.

У даній роботі досліджено 5 основних властивостей, подано метод граничного переходу під знаком інтегралу Стілтьєса та формула, за якою здійснюється інтегрування за частинами цього інтегралу.

Були розглянуті приклади застосування інтеграла Стілтьєса для розв’язку різних класів задач, зокрема, можливість об’єднання однією інтегральною формулою різнорідних випадків неперервно розподілених и зосереджених мас за допомогою інтеграла Стілтъєса.

Отже, слід зазначити, що інтеграл Стілтьєса має специфічні властивості і є не тільки узагальненням інтегралу Рімана, але й самостійним інструментом для розв’язку певного класу задач.

Список використаних джерел

1. Градштейн и Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений.- М.: Наука, 1963 – 312с.

2. Давидов М.О. Курс математчного анализу. Ч. 1. – К.:Вища школа, 1990. – 350с.

3. Канторович Л.В., Акитов Г.Л. Функциональный аналіз. – М.: ИЛ, 1961 – 321с.

4. Кудрявцев Л.Д. Курс математического анализа, т.2. - М.: Высшая школа, 1965. – 369с

5. Никольский С.М. Курс математического анализа - М.: Физматгиз, 2001 – 398с.

6. Макаров И.П. Дополнительные главы математического анализа: учебное поссобие. – М.: Прсвещение, 1968 - 307с.

7. Смирнов В.И. Курс высшей математики (В 5-ти т.) том 5. - М.-Л. АН СССР, 1959 – 452с.

8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (В 3-х томах) т.3. М.: Физматгиз, 1963 - 662с.

[1] Томас Іоанес Стілтьєс (нідерл. Thomas Joannes Stieltjes, 29.12.1856, — 31.12.1894 Тулуза) — нідерландський математик.

Запрпонував у 1894 р. узагальнення визначеного інтегралу (Інтеграл Рімана-Стілтьеса). Член-кореспондент Петербурзької Академії наук (1894).