Кафедра математичного анілізу та інформатики

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Імені В.Г. Короленка

Кафедра математичного анілізу та інформатики

Курсова робота з математики

ІНТЕГРАЛ СТІЛТЬЄСА

Виконала студентка групи М-41

Лозицька Тетяна Петрівна

Науковий керівник

Канд. фіз.-мат. наук, доцент

Кононович Тетяна Олександрівна

Полтава-2008

ЗМІСТ

ВСТУП

§1.Визначення інтегралу Стілтьєса

§2. Існування інтегралу Стілтьєса

2.1. Загальні умови існування інтегралу Стілтьєса.

2.2. Класи випадків існування інтегралу Стілтьєса

§3. Властивості інтегралу Стілтьєса

§4. Інтегрування за частинами

§5.Зведення інтеграла Стілтьєса до інтегралу Рімана

§6. Обчислення інтегралів Стілтьєса

§7. Приклади обчислення інтеграла Стілтьєса

§8.Граничний перехід під знаком інтеграла Стілтьєса

ВИСНОВКИ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ВСТУП

Інтегрування у XIX сторіччі в основному пов’язано з теорією тригонометричних рядів. Інтеграл Стілтьєса виник в зовсім новій, нетрадиційній області, а саме в теорії ланцюгових дробів, залишаючись в межах цієї теорії він був частиною мало помітною, специфічним узагальненням інтеграла Рімана. Таким він був близько 15 років. Ф. Пісс в 1910 р. надрукував замітку, змістом якої була формула, яка виражала інтеграл Стілтьєса від неперервної функції f(x) через інтеграл Лебега від деякої сумовної функції другого аргументу.

Лебег пропонує на основі даного ним представлення інтеграла Стілтьєса визначити інтеграл Стілтьєса від розривної функції. У 1914р. Юнг показав, що метод монотонних послідовностей, застосований до інтеграла Стілтьєса, досить просто призводить до того ж узагальнення.

У зв’язку з переходом в простір більшого числа змінних до кінця сформулювалась точка зору на інтеграл, як на функцію множини. Така точка зору стала особливо родючою для теорії і дозволила серед множини визначень виділити таке поняття диференціювання, в термінах якого ця теорія набуває єдиної форми, незалежно від кількості змінних.

Дана тема представлена в інтегральному численні і вивчається як додатковий розділ курсу математичного аналізу.

Метою роботи є вивчення умов існування, властивостей, методів обчислення інтеграла Стілтьєса. Відповідно до мети поставлені наступні завдання:

1. Ввести означення інтегралу Стілтьєса.

2. Визначити умови його існування та класи інтегрованих за Стілтьєсом функцій.

3. Вивчити процес зведення інтегралу Стілтьєса до інтегралу Рімана.

4. Розглянути приклади обчислення та граничний перехід під знаком інтегралу Стілтьєса

Існування інтегралу Стілтьєса

Інтегрування за частинами

Для інтегралів Стілтьєса має місце формула

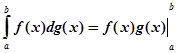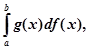– (8)

в припущенні, що існує один з цих інтегралів; існування іншого звідси вже випливає. Ця формула носить назву формули інтегрування за частинами. Доведемо її.

Нехай існує інтеграл 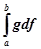. Розклавши проміжок [а, b] на частини [x _i , x_i ₊₁] (i = 0, 1, ..., n — 1), оберемо в цих частинах довільно по точці 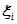таким чином, що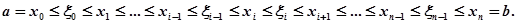

Суму Стілтьєса для інтеграла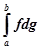

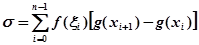
можна представити у вигляді

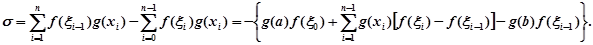
Якщо додати або відняти зправа вираз 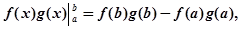то 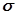перепишеться так:

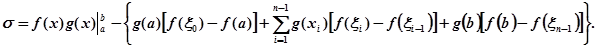
Вираз у фігурних дужках представляє собою стілтьесову суму для інтеграла 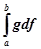(існування якого припущено!). Вона відповідає розбиттю проміжку [а, b] точками ділення 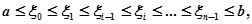якщо в якості обраних з проміжків 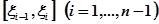точок узяти x_i, а для проміжків 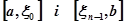, відповідно, а і b. Якщо, як зазвичай, покласти 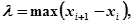то тепер довжини всіх частинних проміжків не перевищать .

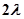При 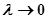сума у квадратних дужках прямує до 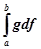, з чого слідує, що існує границя і для 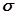, тобто інтеграл 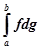і цей інтеграл визначається формулою (9). [8]

Висновки

У даній роботі розглянуто означення і основні властивості інтеграла Стілтьєса, його зв’язок, особливості і відмінності від інших визначених інтегралів.

В ході виконання курсової роботи були з’ясовані загальні умови існування інтегралу Стілтьєса та 3 класи випадків його існування, а також вивчено порядок зведення інтегралу Стілтьєса до інтегралу Рімана.

У даній роботі досліджено 5 основних властивостей, подано метод граничного переходу під знаком інтегралу Стілтьєса та формула, за якою здійснюється інтегрування за частинами цього інтегралу.

Були розглянуті приклади застосування інтеграла Стілтьєса для розв’язку різних класів задач, зокрема, можливість об’єднання однією інтегральною формулою різнорідних випадків неперервно розподілених и зосереджених мас за допомогою інтеграла Стілтъєса.

Отже, слід зазначити, що інтеграл Стілтьєса має специфічні властивості і є не тільки узагальненням інтегралу Рімана, але й самостійним інструментом для розв’язку певного класу задач.

Список використаних джерел

1. Градштейн и Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений.- М.: Наука, 1963 – 312с.

2. Давидов М.О. Курс математчного анализу. Ч. 1. – К.:Вища школа, 1990. – 350с.

3. Канторович Л.В., Акитов Г.Л. Функциональный аналіз. – М.: ИЛ, 1961 – 321с.

4. Кудрявцев Л.Д. Курс математического анализа, т.2. - М.: Высшая школа, 1965. – 369с

5. Никольский С.М. Курс математического анализа - М.: Физматгиз, 2001 – 398с.

6. Макаров И.П. Дополнительные главы математического анализа: учебное поссобие. – М.: Прсвещение, 1968 - 307с.

7. Смирнов В.И. Курс высшей математики (В 5-ти т.) том 5. - М.-Л. АН СССР, 1959 – 452с.

8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (В 3-х томах) т.3. М.: Физматгиз, 1963 - 662с.

[1] Томас Іоанес Стілтьєс (нідерл. Thomas Joannes Stieltjes, 29.12.1856, — 31.12.1894 Тулуза) — нідерландський математик.

Запрпонував у 1894 р. узагальнення визначеного інтегралу (Інтеграл Рімана-Стілтьеса). Член-кореспондент Петербурзької Академії наук (1894).