Доведемо наступну теорему:

1. Якщо функція f(x) інтегрована в сенсі Рімана на проміжку [a, b], a g(x) представлена інтегралом

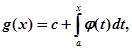
де функція 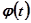 абсолютно інтегровна в [а, b ], то

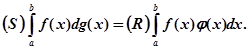                    (11)

Існування інтеграла Стілтьєса при зроблених припущеннях уже було доведено вище.

Залишається лише з’ясувати рівність (11).

Без зменшення загальності можна припустити, що функція 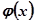 додатна.

Складемо суму Стілтьєса

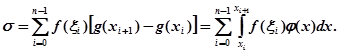
Так як, з іншого боку, можна написати

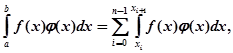
то будемо мати

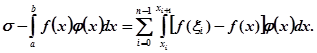
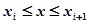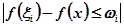Очевидно, для  буде , де 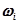означає коливання функції f(x) на проміжку [x_і, x_і+1]. Звідси витікає така оцінка записаної вище різниці:

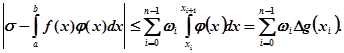
Нам відомо, що при 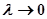 остання сума прямує до 0, з чого слідує, що

,

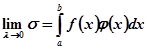що і доводить формулу (11).

2. При тих самих припущеннях стосовно функції f(x) припустимо, що функція g(x) неперервна на всьому проміжку [а, b ] і має в ньому, за виключенням лише скінченої кількості точок, похідну g'(x), яка на [а, b ] абсолютно інтегрована. Тоді

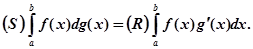          (12)

Звертаючись до випадків, коли функція g ( x ) є розривною розглянемо спочатку «стандартну» розривну функцію р(х), яка визначається рівностями

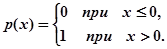
Вона має розрив першого роду — стрибок — у точці х= 0 зправа, причому величина стрибка р(+0) – р(0)) дорівнює 1; в точці х =0 зліва і в решті точок функція p ( x ) неперервна. Функція p ( x – c ) буде мати такий самий розрив у точці x = c зправа; навпаки, p ( с – x ) буде мати подібний розрив у точці x = c зліва, причому величина стрибка дорівнює – 1.

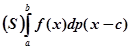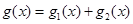Припустимо, що функція f(x) неперервна в точці х = с, і обчислимо інтеграл , де  (при 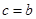 інтеграл рівний нулю).

Складемо суму Стілтьєса:

.

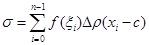Нехай точка 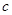 потрапляє, скажімо в 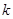-ий проміжок, так що 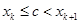. Тоді 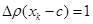, а при 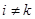, очевидно 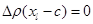. Таким чином, уся сума  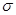зводиться до одного доданку 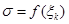. Нехай тепер 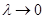. По неперервності 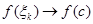. Виходячи з цього, існує (при )

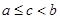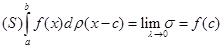       (13)

Аналогічно можна упевнитися в тому, що (при )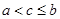

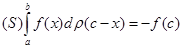               (14)

(при 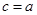 цей інтеграл перетворюється на нуль).

Тепер ми можемо довести дещо узагальнену на відміну від 2, а саме відмовимося від вимоги неперервності функції :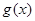

3. Нехай функція f(x) на проміжку 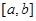 неперервна,a g(x) має на цьому проміжку, виключаючи хіба лише скінчене число точок, похідну  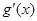яка абсолютно інтегровна на 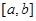. При цьому нехай функція g(x) у скінченому числі точок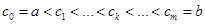

має розрив першого роду. Тоді існує інтеграл Стілтъєса, який виражається формулою

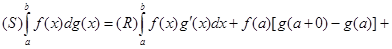
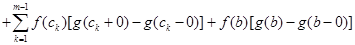. (15)

Характерна тут наявність позаінтегральної суми, де фігурують скачки функції g(x) в точках 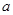 або 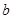 — односторонні. (Якщо на будь-якій з цих функцій стрибка немає, то відповідний доданок суми перетворюється на нуль).

Для спрощення запису введемо позначення для стрибків функції g(x) зправа и зліва:

       ,

       ;

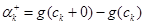
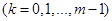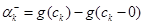
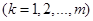очевидно, для , .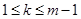

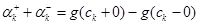Складемо допоміжну функцію:

,

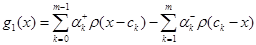Яка як би вбирає у себе усі розриви функції g(x), так що різниця 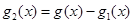, як ми зараз встановимо, виявляється вже неперервною.

Для значень 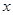 відмінних від усіх 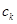, неперервність функції  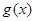не викликає сумнівів, бо для цих значень неперервні обидві функції  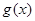и 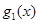. Доведемо тепер неперервність  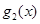у точці  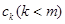зправа. Усі доданки суми 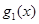, окрім члена 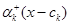, неперервну при  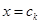зправа, тому достатньо вивчити поведінку виразу 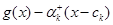. При 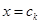 воно має значення 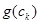; але така ж і його границя при :

.

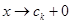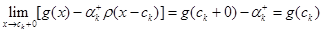Аналогічно перевіряється ф неперервність функції 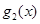 в точці  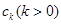зліва.

Далі, якщо взяти точку х (відмінну від усіх 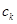), в якій функція  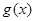має похідну, то поблизу цієї точки  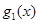зберігає постійне значення, виходячи з цього, у ній і функція  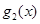має похідну, причому .

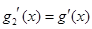Для неперервної функції 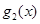, за попередньою теоремою, існує інтеграл Стілтьєса .

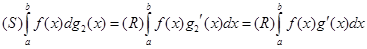Так само легко обрахувати і інтеграл

.

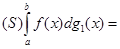
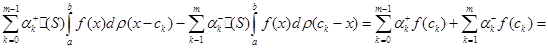
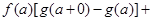
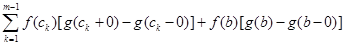Додаючи почленно ці дві рівності, ми і прийдемо до рівності (15); існування інтеграла Стілтьєса від 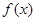 по функції  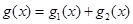встановлюється попутно. [5]