З визначення інтегралу Стілтьєса безпосередньо випливають такі його властивості:

1. ;

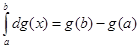2. ;

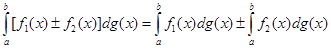3. ;

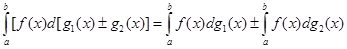4. .

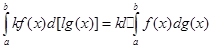
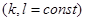При цьому у випадках 2, 3, 4 з існування інтегралів у правій частині випливає існування інтеграла у лівій частині. Далі маємо

5. ,

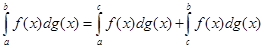у припущенні, що 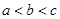 і існують всі три інтеграли.

Для доведення цієї формули достатньо включити точку с в число точок розбиття проміжку 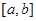, при складанні суми Стілтьєса для інтегралу .

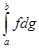Перш за все, з існування інтеграла 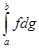 уже випливає існування обох інтегралів  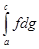і .

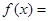
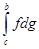Для своєрідного граничного процесу, за допомогою якого для стілтьєсової суми отримується інтеграл Стілтьєса, має місце принцип збіжності Больцано-Коші. Таким чином по заданому 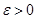 враховуючи існування інтеграла  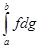знайдеться таке 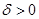, що будь-які дві суми  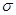і 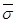, яким відповідають  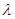і 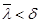, різняться менш ніж на 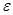. Якщо при цьому у склад точок розбиття включити точку с, а точки розбиття, що припадають на проміжок 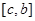, брати в обох випадках одними й тими самими, то різниця  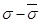зведеться до різниці  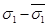двох сум Стілтьєса, що належать вже проміжку 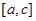, бо решта доданків взаємно скорочуються. Застосовуючи до проміжку  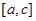і обрахованим для нього стілтьєсовим сумам той же принцип збіжності, зробимо висновок про існування інтеграла 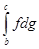. Аналогічним чином встановлюється і існування інтегралу 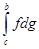. Але, важливо відмітити, що з існування обох інтегралів  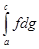і 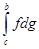, взагалі кажучи, не випливає існування інтегралу 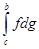. Щоб упевнитися в цьому, достатньо розглянути приклад. Нехай на проміжку  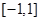функції  і 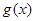 задані наступними рівностями:

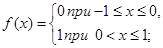
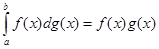
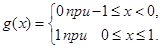
Легко побачити, що інтеграли

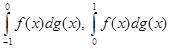
обидва існують і рівні 0, бо відповідні суми Стілтьєса всі рівні 0: для першого це випливає з того, що завжди 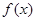=0, для другого – з постійності функції 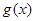, завдяки чому 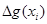=0.

У той же час інтеграл 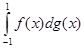 не існує. Дійсно, розіб’ємо проміжок  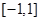так, щоб точка 0 не потрапила у склад точок розбиття, і складемо суму:

.

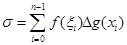Якщо точка 0 потрапляє в проміжок 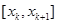, так, що 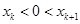, то в сумі  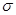залишиться лише один 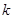-й доданок; решта будуть нулі, тому що  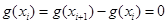для 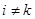. Отже,

.

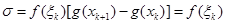В залежності від того, чи буде 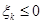 або 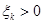, виявиться  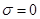або 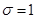, так що  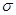границі не має

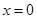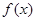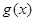Вказана своєрідна умова пов’язана з наявністю розривів у точці  для обох функцій  і . [8]

Інтегрування за частинами

Для інтегралів Стілтьєса має місце формула

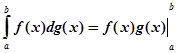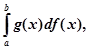–      (8)

в припущенні, що існує один з цих інтегралів; існування іншого звідси вже випливає. Ця формула носить назву формули інтегрування за частинами. Доведемо її.

Нехай існує інтеграл 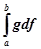. Розклавши проміжок [а, b] на частини [x _i , x_{i +1}] (i = 0, 1, ..., n — 1), оберемо в цих частинах довільно по точці  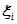таким чином, що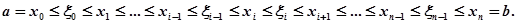

Суму Стілтьєса для інтеграла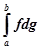

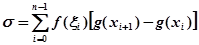
можна представити у вигляді

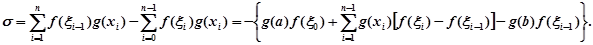
Якщо додати або відняти зправа вираз 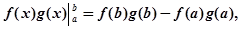 то 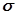 перепишеться так:

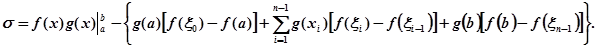
Вираз у фігурних дужках представляє собою стілтьесову суму для інтеграла 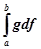(існування якого припущено!). Вона відповідає розбиттю проміжку [а, b] точками ділення  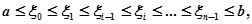якщо в якості обраних з проміжків  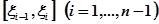точок узяти x_i, а для проміжків 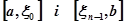, відповідно, а і b. Якщо, як зазвичай, покласти  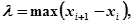то тепер довжини всіх частинних проміжків не перевищать .

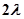При 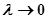 сума у квадратних дужках прямує до 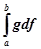, з чого слідує, що існує границя і для 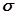, тобто інтеграл  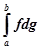і цей інтеграл визначається формулою (9). [8]