Прямий вибір - повторюваний пошук найменшого елемента серед N елементів, N-1 елементів, N-2 і т.д. Кількість порівнянь при цьому (N2-N)/2. Для підвищення ефективності необхідно залишати після кожного етапу побільше інформації окрім ідентифікації найменшого ключа.
Після N/2 порівнянь можна знайти в кожній парі елементів найменший, після N/4 порівнянь - менший із пари вже вибраних на попередньому кроці і т.д. Виконавши загалом N/2+N/4+...+2+1=N-1 порівнянь, можна побудувати дерево вибору та ідентифікувати його корінь як шуканий найменший елемент. Наприклад
крок I \ / \ / \ / \ /
44 12 06
крок II \ / \ /
12 06
крок III \ /
06
На наступному етапі сортування проводиться рух вздовж віток, які відмічені мінімальними елементом, і вилучення його з дерева шляхом заміни на пустий елемент.
44[]
\ / \ / \ / \ /
44 12 18 []
\ / \ /
12 []
\ /
[]
Далі здійснюється заповнення "дірок" у дереві. На першому рівні залишається "дірка" від вилученого елемента, а на наступних знову вибирається менший із двох сусідніх попереднього рівня. "Дірка" при порівнянні вважається як завгодно великим значенням.
44[]
\ / \ / \ / \ /
44 12 18 67
\ / \ /
12 18
\ /
12
Елемент, що опинився в корені, - знову найменший. Після N таких кроків дерево стане пустим, в ньому будуть лише одні "дірки" (сортування закінчене). На кожному з N етапів виконується log(N) порівнянь. Тому на весь процес впорядкування потрібно порядку N*log(N) операцій плюс N-1 операцій для побудови дерева. Це значно краще ніж N2 для прямих методів і навіть краще ніж N1,2 для алгоритму Шелла. Однак при цьому виникає проблема збереження додаткової інформації. Тому кожен окремий етап в алгоритмі ускладнюється.
Корисно було б, зокрема, позбутися від "дирок", якими вкінці буде заповнене все дерево, і які породжують багато непотрібних порівнянь. Крім того, виникає потреба такої організації даних за принципом дерева, яка б вимагала N одиниць пам’яті, а не 2N-1. Цього вдалося добитися в алгоритмі Heap Sort, який розробив Д. Уілльямс. Він використав спеціальну деревовидну структуру - піраміду.
Піраміда - це означене, тобто задане елементами кореневе бінарне дерево, яке визначається як послідовність ключів a L , a L+1 , ..., a R , для якої справедливі нерівності
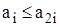 та
та 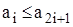 для
для 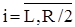 .(1)
.(1)
Таким чином бінарне дерево сортувань виду
a1
/ \
a2=42a3=06
/ \ / \
a4=55a5=94a6=18a7=12
являє собою піраміду, а елемент a1 буде найменшим в розглядуваній множині : a1=min(a 1 , a 2 , ..., a N).
Припустимо, що є деяка піраміда із заданими елементами a L+1 , ..., a R для певних значень L та R, і потрібно ввести новий елемент x, утворюючи таким чином розширену піраміду a L , a L+1 , ..., a R . В якості вихідної візьмемо піраміду a 1 , a 2 , ..., a 7 із попереднього прикладу і добавимо до неї зліва елемент a 1=44. Нова піраміда отримується так : спочатку x ставиться зверху деревовидної структури, а потім він поступово опускається вниз кожен раз в напрямку меншого з двох прилеглих до нього елементів, а сам цей менший елемент переміщується вгору. Процес просіювання продовжується доти, поки в жодній з прилеглих вершин не буде елемента меншого за нововведеного. В розглядуваному прикладі ключ 44 спочатку поміняється місцями з ключем 06, а потім з 12, і в результаті отримується таке дерево
06
/ \
42
/ \ / \
94 18
Характерно, що такий метод просіювання залишає незмінними умови (1), які визначають піраміду.
Р. Флойд запропонував певний "лаконічний" алгоритм побудови піраміди "на тому ж місці". Вважається, що деяка частина елементів масиву a m , a 2 , ..., a N (m=Ndiv2) вже утворює піраміду - нижній шар відповідного бінарного дерева, для них ніякої впорядкованості не вимагається. Тепер піраміда розширюється вліво; кожен раз добавляється і просіюваннями ставитться у відповідну позицію новий елемент. Ці дії реалізуються проседурою Sift :
Procedure Sift(L, R : integer);
Var
i, j : integer; x : basetype;
Begin
i:=L; j:=2*L; x:=a[L];
if (j<R) and (a[j+1]<a[j]) then j:=j+1;
while (j<=R) and (a[j]<x) do
Begin
a[i]:=a[j]; a[j]:=x; i:=j; j:=2*j;
if (j<R) and (a[j+1]<a[j]) then j:=j+1
End
End;
Таким чином, процес формування піраміди із N елементів a 1 , ..., a N "на тому ж місці" є повторюваним виконанням процедури Sift при зміні параметра L=Ndiv2, ..., 1 :
L:=N div 2 +1;
while L>1 do
Begin
L:=L-1;
Sift(L, N)
end;
Для ілюстації алгоритму розглянемо попередній варіант масиву :
44 |
44 |
44 |
44 | 42
06
Тут жирним шрифтом виділені добавлювані до піраміди елементи; підкреслені - елементи, з якими проводився обмін.
Для того, щоб отримати не тільки часткове, а і повне впорядкування серед елементів послідовності, потрібно виконати N зсувних етапів. Після кожного проходу на вершину дерева виштовхуватиметься черговий найменший ключ. Знову виникає питання : де зберігати "спливаючі" верхні елементи і чи можна проводити перестановки "на тому ж місці"? Це легко реалізувати, якщо кожен раз брати останню компоненту піраміди - це буде просіюваний ключ x, ховати верхній елемент з попереднього етапу в звільнене позицію, а x зсувати на відповідне місце. Зрозуміло, що після кожного етапу розглядувана піраміда буде скорочуватися на один елемент справа. Таким чином, впорядкування масиву буде здійснено за N-1 прохід :
06 42 12 55 94 18 44 67обмін 67 і 06
67 42 12 55 94 18 44 | 06просіювання 67
12 42 18 55 94 67 44 | 06обмін 44 і 12
44 42 18 55 94 67 | 12 06просіювання 44
18 42 44 55 94 67 | 12 06обмін 67 і 18
67 42 44 55 94 | 18 12 06просіювання 67
42 55 44 67 94 | 18 12 06обмін 94 і 42
94 55 44 67 | 42 18 12 06просіювання 94
44 55 94 67 | 42 18 12 06обмін 67 і 44
67 55 94 | 44 42 18 12 06просіювання 67
55 67 94 | 44 42 18 12 06обмін 94 і 55
94 67 | 55 44 42 18 12 06просіювання 94
67 94 | 55 44 42 18 12 06обмін 94 і 67
94 | 67 55 44 42 18 12 06просіювання 94
94 | 67 55 44 42 18 12 06
Тут жирним шрифтом виділені просіювані по піраміді елементи; підкреслені - елементи, між якими проводився обмін.
Процес сортування описується за допомогою процедури Sift таким чином:
R:=N;
while R>1 do
Begin
x:=a[1]; a[1]:=a[R]; a[R]:=x;
R:=R-1;
Sift(1, R)
End;
Як видно з прикладу, отриманий порядок ключів фактично є зворотнім. Це легко виправити, помінявши напрямок відношення порівняння в процедурі Sift на протилежний. Остаточно процедура сортування масиву методом Heap Sort матиме вигляд :
Procedure Heap_Sort;
Var
L, R : integer; x : basetype;
Procedure Sift(L, R : integer);
Var
i, j : integer; x : basetype;
Begin
i:=L; j:=2*L; x:=a[L];
if (j<R) and (a[j]<a[j+1]) then j:=j+1;
while (j<=R) and (x<a[j]) do
Begin
a[i]:=a[j]; a[j]:=x; i:=j; j:=2*j;
if (j<R) and (a[j]<a[j+1]) then j:=j+1
End
End;
Begin
L:=N div 2 +1; R:=N;
while L>1 do
begin L:=L-1; Sift(L, N) end;
while R>1 do
Begin
x:=a[1]; a[1]:=a[R]; a[R]:=x;
R:=R-1;
Sift(1, R)
End
End;
Аналіз алгоритму Heap Sort. Як вже раніше відмічалося, складність алгоритму по операціях порівняння є величиною порядку O(N*log(N)+N). Кількість переміщень елементів суттєво залежить від стартового розміщення ключів в послідовності.
Однак при початково-впорядкованому масиві не слід чекати максимальної ефективності. Адже об’єм перестановок в цьому випадку є досить великим під час просіювання "важких" елементів після побудови піраміди. Фактично на кожному етапі такого просіювання виконується log(K) перестановок плюс ще N-1 обмін перед просіюванням, де K - кількість елементів в піраміді, в якій проводиться просіювання. Таким чином, в цьому випадку
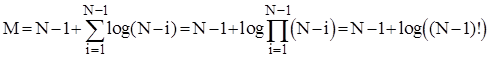 .
.
Тому можна вважати, що розглядуваний метод як і по порівняннях так і по перестановках має ефективність порядку O(N*log(N)+N).
Дата: 2019-05-28, просмотров: 279.