Зміст
Вступ
Розділ І. Прямі методи сортування масивів
1.1 Сортування прямим включенням
1.2 Сортування бінарним включенням
1.3 Сортування прямим вибором
1.4 Сортування прямим обміном
Розділ ІІ. Швидкі методи сортування масивів
2.1 Сортування включенням із зменшуваними відстанями – алгоритм Шелла (1959)
2.2 Сортування обміном на великих відстанях – алгоритм Quick Sort
2.3 Сортування вибором при допомозі дерева – алгоритм Тree Sort
2.4 Сортування вибором при допомозі дерева – алгоритм Heap Sort
2.5 Порівняльна характеристика швидкодії деяких швидких алгоритмів сортування
Висновки
Література
Вступ
В наш час нові інформаційні технології посідають дуже важливе місце не лише в спеціалізованих, але й в повсякденних сферах життя. Комп’ютери застосовуються в бізнесі, менеджменті, торгівлі, навчанні та багатьох інших сферах діяльності людини.
Комп’ютерні технології дуже зручні для виконання різноманітних операцій, але в різних сферах застосування ці операції різні. Тому, кожна окрема галузь, яка використовує специфічні технічні засоби, потребує своїх власних програм, які забезпечують роботу комп’ютерів.
Розробкою програмного забезпечення займається така галузь науки, як програмування. Вона набуває все більшого й більшого значення останнім часом, адже з кожним днем комп’ютер стає все більш необхідним, все більш повсякденним явищем нашого життя. Адже обчислювальна техніка минулих років вже майже повністю вичерпала себе і не задовольняє тим потребам, що постають перед людством.
Таким чином, нові інформаційні технології дуже актуальні в наш час і потребують багато уваги для подальшої розробки та вдосконалення. Поряд з цим, велике значення має також і програмування, яке є одним із фундаментальних розділів інформатики і тому не може залишатись осторонь.
Програмування містить цілу низку важливих внутрішніх задач. Однією з найбільш важливих таких задач для програмування є задача сортування. Під сортуванням звичайно розуміють перестановки елементів будь-якої послідовності у визначеному порядку. Ця задача є однією з найважливіших тому, що її метою є полегшення подальшої обробки певних даних і, насамперед, задачі пошуку. Так, одним з ефективних алгоритмів пошуку є бінарний пошук. Він працює швидше ніж, наприклад, лінійний пошук, але його можливо застосовувати лише за умови, що послідовність вже упорядкована, тобто відсортована.
Взагалі, відомо, що в будь-якій сфері діяльності, що використовує комп’ютер для запису, обробки та збереження інформації, усі дані зберігаються в базах даних, які також потребують сортування. Певна впорядкованість для них дуже важлива, адже користувачеві набагато легше працювати з даними, що мають певний порядок. Так, можна розташувати всі товари по назві або відомості про співробітників чи студентів за прізвищем або роком народження, тощо.
Задача сортування в програмуванні не вирішена повністю. Адже, хоча й існує велика кількість алгоритмів сортування, все ж таки метою програмування є не лише розробка алгоритмів сортування елементів, але й розробка саме ефективних алгоритмів сортування. Ми знаємо, що одну й ту саму задачу можна вирішити за допомогою різних алгоритмів і кожен раз зміна алгоритму приводить до нових, більш або менш ефективних розв’язків задачі. Основними вимогами до ефективності алгоритмів сортування є перш за все ефективність за часом та економне використання пам’яті. Згідно цих вимог, прості алгоритми сортування (такі, як сортування вибором і сортування включенням) не є дуже ефективними.
Алгоритм сортування обмінами, хоча і завершує свою роботу (оскільки він використовує лише цикли з параметром і в тілі циклів параметри примусово не змінюються) і не використовує допоміжної пам’яті, але займає багато часу. Навіть, якщо внутрішній цикл не містить жодної перестановки, то дії будуть повторюватись до тих пір, поки не завершиться зовнішній цикл.
Алгоритм сортування вибором ефективніше сортування обмінами за критерієм М(n), тобто за кількістю пересилань, але також є не дуже ефективним. З цих причин було розроблено деякі нові алгоритми сортування, що отримали назву швидких алгоритмів сортування. Це такі алгоритми, як сортування деревом, пірамідальне сортування, швидке сортування Хоара та метод цифрового сортування.
Метою нашої дослідницької роботи є ознайомлення з цими швидкими алгоритмами сортування, спроба проаналізувати їх і висвітлити кожен з них і написати програму, яка б виконувала сортування деякої послідовності за допомогою різних швидких алгоритмів сортування.
Сортування варто розуміти, як процес перегрупування заданої множини об'єктів в деякому конкретному порядку. Мета сортування - полегшити наступний пошук елементів в такій відсортованій множині.
Вибір алгоритму залежить від структури даних, що обробляються. У випадку сортування ця залежність настільки велика, що відповідні методи навіть були розбиті на дві групи - сортування масивів і сортування файлів (послідовностей). Іноді їх називають внутрішнім і зовнішнім і сортуванням, оскільки масиви зберігаються в швидкій внутрішній пам’яті (оперативній) із довільним доступом, а файли розміщуються в менш швидкій, проте більш об'ємній зовнішній пам'яті.
Метод сортування називається стійким, якщо в процесі впорядкування відносне розміщення елементів з рівними значеннями не міняється. Стійкість сортування часто буває бажаною, якщо йде мова про елементи, що вже впорядковані по деяких вторинних ключах (тобто ознаках), які не впливають на основний ключ.
Нехай дано масив N елементів деякого абстрактного типу basetype:
a : array [1..N] of basetype.
Не обмежуючи загальності, зупинимося на впорядкуванні його компонентів по зростанню.
Основна умова: обраний метод сортування масивів повинен економно використовувати доступну пам’ять. Це означає, що перестановки, які приводять елементи в порядок, повинні виконуватися "на тому ж місці". Тобто методи, в яких елементи масиву a передаються в результуючий масив b, не мають практичної цінності.
Алгоритми сортування окрім критерію економії пам’яті будуть класифікуватися по швидкості, тобто по часу їх роботи. Оскільки на різних типах ЕОМ одні і ті ж методи показуватимуть відмінні результати, то в якості міри ефективності алгоритму можуть бути прийняті числа: C - кількість необхідних порівнянь ключів; M - кількість перестановок елементів. Очевидно, що ці числа є функціями від кількості елементів в масиві N. Згідно із введеними критеріями швидкодії алгоритми сортування поділяють на два типи - прямі та швидкі.
Прямі методи зручні для пояснення і розбору основних рис більшості сортувань, легко програмуються і відлагоджуються, а самі програми - короткі, що теж важливо для економії пам’яті. В основі їх лежить повторення N етапів обробки масиву із зменшенням на кожному з них кількості порівнюваних елементів. Ефективність даних алгоритмів є величиною порядку O(N2). Такі методи зручно використовувати на так званих "коротких" масивах.
Швидкі методи вимагають невеликої кількості етапів обробки, однак ці етапи досить складні. На кожному з них окрім переміщення чергового елемента на "своє" місце відбувається перегрупування решти відносно цього елемента. Звичайно виграш по ефективності для таких алгоритмів отримується на "довгих" масивах.
Методи сортування "на тому ж місці" у відповідності із визначаючими їх принципами розбиваються на три основні категорії :
- сортування включенням;
- сортування вибором;
- сортування обміном.
У курсовій роботі ми детально розглянемо швидкі алгоритми сортування елементів масиву, проведемо їх порівняльний аналіз. Крім цього, розглянемо і прямі методи сортування, їх позитиви і недоліки, що дасть змогу краще визначити ефективність і складність швидких алгоритмів сортування.
Begin
x:=a[i];
включення x на потрібне місце серед a[1], ..., a[i]
end;
Процес просіювання (пошуку потрібного місця для включення елемента x ) може припинитися при виконанні однієї із двох умов :
1) знайдено елемент a j з ключем, меншим ніж ключ у x ;
2) досягнутий лівий кінець "готової" послідовності.
Таким чином програмна реалізація методу прямого включення матиме вигляд процедури :
Procedure Straight_Insertion;
Var
i, j : integer; x : basetype;
Begin
for i:=2 to N do
Begin
x:=a[i]; a[0]:=x; j:=i;
while x<a[j-1] do
Begin
a[j]:=a[j-1];
j:=j-1
end;
a[j]:=x
End
End;
Використання додаткового елемента в масиві - "бар’єра" a[0]=x забезпечує гарантоване припинення процесу просіювання. Це дозволяє зменшити кількість логічних умов в заголовку цикла while до однієї, а кількість логічних операцій від 2i-1 до i на кожному етапі. Звичайно, при цьому необхідно попередньо розширити на один елемент масив a та діапазон допустимих значень індекса. На жаль, таке покращення ефективності по кількості порівнянь не зменшує об’єму перестановок елементів.
Аналіз прямого включення. Кількість порівнянь ключів Ci при i-ому просіюванні найбільше дорівнює i, найменше - 1, а середньоймовірна кількість - i/2. Кількість же перестановок (переприсвоєнь ключів), включаючи бар’єр, Mi=Ci+2. Тому для оцінки ефективності алгоритму у випадках початково впорядкованого, зворотньо впорядкованого та довільного масиву можна скористатися наступними співвідношеннями:
; 
;
;
;
;
.
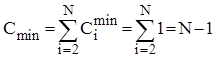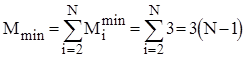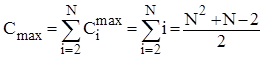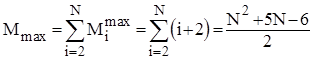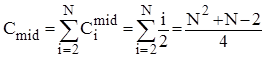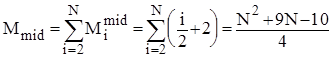Очевидно, що розглянутий алгоритм описує процес стійкого сортування.
Var
i, j, m, L, R : integer; x : basetype;
Begin
for i:=2 to N do
Begin
x:=a[i]; L:=1; R:=i;
while L<R do
Begin
m:=(L+R) div 2;
if a[m]<=x then L:=m+1 else R:=m
end;
for j:=i downto R+1 do
a[j]:=a[j-1];
a[R]:=x
End
End ;
Аналіз бінарного включення. Зрозуміло, що кількість порівнянь у такому алгоритмі фактично не залежить від початкового порядку елементів. Місце включення знайдено, якщо L=R. Отже вкінці пошуку інтервал повинен бути одиничної довжини. Таким чином ділення його пополам на i-ому етапі здійснюється log(i) раз. Тому кількість операцій порівняння буде:
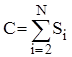, де 
, 
.
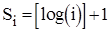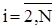Апроксимуючи цю суму інтегралом, отримаємо наступну оцінку :
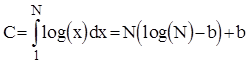, де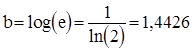 
.
Однак істинна кількість порівнянь на кожному етапі може бути більшою ніж log(i) на 1. Тому
.
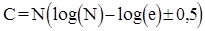Нажаль покращення, що породженні введенням бінарного пошуку, стосується лише кількості операцій порівняння, а не кількості потрібних переміщень елементів. Фактично кількість перестановок M залишається величиною порядку N2. Для досить швидких сучасних ЕОМ рух елемента, тобто самого ключа і зв’язаної з ним інформації, займає значно більше часу, ніж порівняння самих ключів. Крім того сортування розглядуваним методом вже впорядкованого масиву за рахунок log(i) операцій порівняння вимагатиме більше часу, ніж у випадку послідовного сортування з прямим включенням. Очевидно, що кращий результат дадуть алгоритми, де перестановка, нехай і на велику відстань, буде пов’язана лише з одним елементом, а не з переміщенням на одну позицію цілої групи.
Сортування прямим вибором
На відміну від включення, коли для чергового елемента відшукувалося відповідне місце в "готовій" послідовності, в основу цього методу покладено вибір відповідного елемента для певної позиції в масиві. Цей прийом базується на таких принципах :
1) на i-ому етапі серед елементів a i , a i+1 , ..., a N вибирається елемент з найменшим ключем a min ; 2) проводиться обмін місцями a min та a i .
Процес послідовного вибору і перестановки проводиться поки не залишиться один єдиний елемент - з самим найбільшим ключем.
Такий алгоритм можна записати у вигляді послідовності команд :
for i:=1 to N-1 do
Begin
k:=номер найменшого ключа серед a[i], ..., a[N];
обмін місцями a[k] та a[i]
End;
А програмна реалізація методу прямого вибору матиме вигляд процедури
Procedure Straight_Selection;
Var
i, j, k : integer; x : basetype;
Begin
for i:=1 to N-1 do
Begin
x:=a[i]; k:=i;
for j:=i+1 to N do
if a[j]<x then begin x:=a[j]; k:=j end;
x:=a[k]; a[k]:=a[i]; a[i]:=x
End
End;
Аналіз прямого вибору. Очевидно, що кількість порівнянь ключів Ci на i-ому виборі не залежить від початкового розміщення елементів і дорівнює N- i. Таким чином
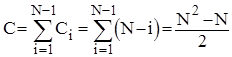
Кількість же перестановок залежить від стартової впорядкованості масиву. Це стосується переприсвоєнь у внутрішньому циклі по j при пошуку найменшого ключа.
В найкращому випадку початково впорядкованого масиву Mi=4 ; в найгіршому випадку зворотно впорядкованого масиву Mi=Ci+4 ; для довільного масиву рівномовірно можливе значення Mi=Ci/2+4. Тому для оцінки ефективності алгоритму по перестановках можна скористатися наступними співвідношеннями:
;
;
.
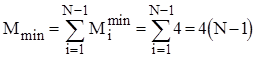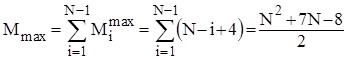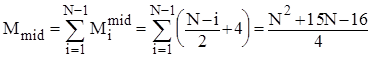Як і в попередньому випадку алгоритм прямого вибору описує процес стійкого сортування.
Сортування прямим обміном
Даний метод базується на повторенні етапів порівняння сусідніх ключів при русі вздовж масиву. Якщо наступний елемент виявиться меншим від попереднього, то відбувається обмін (звідси і назва методу). Таким чином, при русі з права наліво за один етап найменший ключ переноситься на початок масиву. Зрозуміло, що кожен наступний прохід можна закінчувати після позиції знайденого на попередньому етапі мінімального елемента, оскільки всі елементи перед ним вже впорядковані. Розглядуваний процес дещо нагадує виштовхування силою Архімеда бульбашки повітря у воді. Тому цей алгоритм ще називають "бульбашковим" сортуванням.
Програмна реалізація методу прямого обміну або "бульбашки" матиме вигляд процедури:
Procedure Buble_Sort;
Var
i, j : integer; x : basetype;
Begin
for i:=2 to N do
for j:=N downto i do
if a[j-1]>a[j] then begin x:=a[j]; a[j]:=a[j-1]; a[j-1]:=x end
End;
Якщо етапи порівняння та обміну проводити зліва направо, то відбуватиметься виштовхування найбільшого елемента вкінець масиву. Очевидно такий процес відповідає опусканню під дією сили тяжіння камінця у воді. Назвемо цей алгоритм "камінцевим" сортуванням :
Procedure Stone_Sort;
Var
i, j : integer; x : basetype;
Begin
for i:=1 to N-1 do
for j:=1 to N-i do
if a[j]>a[j+1] then begin x:=a[j]; a[j]:=a[j+1]; a[j+1]:=x end
End;
Обидва алгоритми згідно із визначаючим принципом вимагають досить великої кількості обмінів. Тому виникає питання, чи не вдасться підвищити їх ефективність хоча б за рахунок зменшення операцій порівняння? Цього можна добитися при допомозі наступних покращень:
1) фіксувати, чи були перестановки в процесі деякого етапу. Якщо ні, то - кінець алгоритму ;
2) фіксувати крім факту обміну ще і положення (індекс) останнього обміну. Очевидно, що всі елементи перед ним або після нього відповідно для сортування "бульбашкою" або "камінцем" будуть впорядковані ;
3) почергово використовувати алгоритми "бульбашки" і "камінця". Тому що для чистої "бульбашки" за один прохід "легкий" елемент виштовхується на своє місце, а "важкий" опускається лише на один рівень. Аналогічна ситуація з точністю до навпаки і для "камінця". Такий алгоритм називається "шейкерним" сортуванням.
Читачу пропонується самостійно модифікувати наведені вище процедури з врахуванням цих покращень.
Аналіз прямого обміну. Розглянемо спочатку чисту "бульбашку". Для "камінця" оцінки будуть такими ж самими. Зрозуміло, що кількість порівнянь ключів Ci на i-ому проході не залежить від початкового розміщення елементів і дорівнює N-i. Таким чином
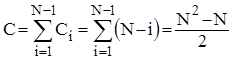
Кількість же перестановок залежить від стартової впорядкованості масиву. В найкращому випадку початково впорядкованого масиву Mi=0 ; в найгіршому випадку зворотньо впорядкованого масиву Mi=Ci*3; для довільного масиву рівноймовірно можливе значення Mi=Ci*3/2. Тому для оцінки ефективності алгоритму по перестановках можна скористатися наступними співвідношеннями:
;
;
.
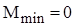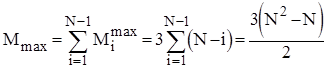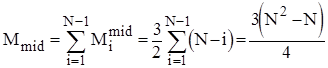Очевидно, що і цей алгоритм, аналогічно з іншими прямими методами, описує процес стійкого сортування.
Розглянемо тепер покращений варіант "шейкерного" сортування. Для цього алгоритму характерна залежність кількості операцій порівняння від початкового розміщення елементів в масиві. В найкращому випадку вже впорядкованої послідовності ця величина буде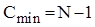 
. У випадку зворотньо впорядкованого масиву вона співпадатиме з ефективністю для чистої "бульбашки".
Як видно, всі покращення не змінюють кількості переміщень елементів (переприсвоєнь), а лише зменшують кількість повторюваних порівнянь. На жаль операція обміну місцями елементів в пам’яті є "дорожчою" ніж порівняння ключів. Тому очікуваного виграшу буде небагато. Таким чином "шейкерне" сортування вигідне у випадках, коли відомо, що елементи майже впорядковані. А це буває досить рідко.
Var
m, i, j, k : integer;
h : array [1..t] of integer;
x : basetype;
Begin
h[1]:=8; h[2]:=4; h[3]:=2; h[4]:=1;
for m:=1 to t do
Begin
k:=h[m];
for i:=k+1 to N do
Begin
x:=a[i]; j:=i-k;
while (x<a[j]) and (j>0) do
Begin
a[j+k]:=a[j]; j:=j-k
end;
a[j+k]:=x
End
End
End;
Аналіз алгоритму Шелла . Поки що не має чітко обгрунтованих виборів відстаней, які давали б найкращу ефективність. Самим цікавим є те, що ці відстані не повинні бути множниками один одного, а тим більше степенями деяких чисел. Це дозволяє уникнути явища, коли на певному етапі взаємодіють дві групи, які до цього ніде ще не перетиналися. Взагалі, бажано, щоб взаємодія окремих ланцюгів відбувалася якомога частіше. Вірною є наступна теорема :
Теорема. Якщо k-відсортовану послідовність i-відсортувати, то вона при цьому залишиться k-відсортованою.
Кнут рекомендує використовувати такі послідовності відстаней, записані в зворотньому порядку :
1, 4, 13, 40, 121, ... , де h i-1=3 h i+1 , h t=1 , t=[ log 3 N]-1 , або
1, 3, 7, 15, 31, ... , де h i-1=2 h i+1 , h t=1 , t=[ log 2 N]-1.
З обчислювальної практики відомо, що загалом метод Шелла має ефективність порядку O(N1,2).
Var
k, L, R, i, j : integer;
x : basetype;
left, right : array [1..N] of integer;
Begin
k:=1; left[k]:=1; right[k]:=N;
while k>0 do
Begin
L:=left[k]; R:=right[k]; k:=k-1;
while R-L>S do
Begin
i:=L; j:=R; x:=a[i];
while j>i do
Begin
while x<a[j] do j:=j-1;
if j>i then begin
a[i]:=a[j]; a[j]:=x; i:=i+1
end;
while a[i]<x do i:=i+1;
if j>i then begin
a[j]:=a[i]; a[i]:=x; j:=j-1
End
end;
k:=k+1;
if R-i<=i-L then
Begin
left[k]:=i+1; right[k]:=R; R:=i-1
End
Else
Begin
left[k]:=L; right[k]:=i-1; L:=i+1
End
end;
for i:=L+1 to R do
Begin
x:=a[i]; j:=i-1;
while (x<a[j]) and (j>=L) do
Begin
a[j+1]:=a[j]; j:=j-1
end;
a[j+1]:=x
End
End
End ;
Аналіз алгоритму Quick Sort. Щоб оцінити ефективність алгоритму, позначимо через Q(N) середню кількість кроків, необхідних для впорядкування N елементів. Припустимо також, S=1, тобто не використовується сортування прямими методами на коротких послідовностях.
При першому проходженні Quick Sort порівнює всі елементи з ведучим і виконується не більше ніж за C*N кроків, де C - деяка константа. Потім потрібно відсортувати дві підпослідовності довжинами I-1 та N-I. Тому середня кількість кроків, потрібних для впорядкування N елементів, залежить від середньої кількості кроків, потрібних для впорядкування I-1 та N-I елементів відповідно. Оскільки всі можливі значення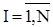 
є рівноймовірними, то спрведлива наступна оцінка :
.
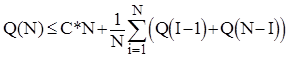Врахувавши, що
,
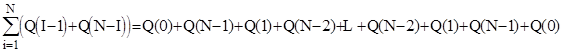отримаємо
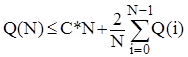.(1)
Покажемо за індукцією по N, що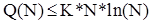 
для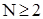 
, де K=2C+2B, B=Q(0)=Q(1). Останнє співвіднощення означає, що Quick Sort вимагає постійної однакової кількості кроків для впорядкування 0 або 1 елемента.
1) N=2 :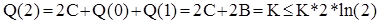 
;
2) припустимо, що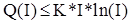 
для I=2, 3, ..., N-1 ;
3) перевіримо справедливість для I=N. Співвідношення (1) з врахуванням попереднього припущення можна переписати у вигляді
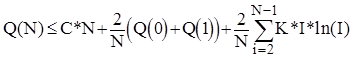або
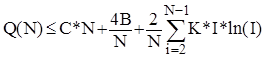.(2)
Оскільки функція I*ln(I) є опуклою вниз, то для цілих значень аргументу справедлива оцінка
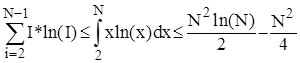
Врахувавши останню нерівність, із співвідношення (2) одержимо
.
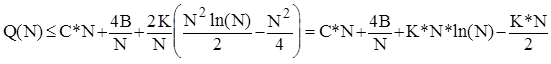Оскільки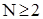 
, то
.
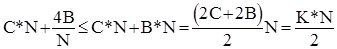Остаточно отримаємо
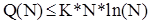.(3)
Таким чином ефективність алгоритму Quick Sort є величина порядку O(N*ln(N)).
Всі наведені викладки справедливі для аналізу по операціях порівняння. Кількість же перестановок залежить від початкового розміщення елементів у послідовності. Характерно, що для цього методу у випадку зворотньо впорядкованого масиву об’єм переміщень ключів не буде максимальним. Адже на кожному етапі ведучий елемент буде найбільшим і опиниться на своєму місці після першого ж порівняння і перестановки, тобто M=N-1. Максимальна кількість переприсвоєнь ключів співпадатиме з кількістю порівнянь, мінімальна - рівна нулю.
Алгоритм Quick Sort, як і розглянуті прямі методи, описує процес стійкого сортування.
End;
Обґрунтування правильності алгоритму очевидно, оскільки кожне чергове просівання викидає в масив У найменший з елементів масиву А, що залишилися.
Сортуюче дерево можна реалізувати, використовуючи або двовимірний масив, або одномірний масиві ST[1..N], де N = 2n-1.
Var
i, j : integer; x : basetype;
Begin
i:=L; j:=2*L; x:=a[L];
if (j<R) and (a[j+1]<a[j]) then j:=j+1;
while (j<=R) and (a[j]<x) do
Begin
a[i]:=a[j]; a[j]:=x; i:=j; j:=2*j;
if (j<R) and (a[j+1]<a[j]) then j:=j+1
End
End;
Таким чином, процес формування піраміди із N елементів a 1 , ..., a N "на тому ж місці" є повторюваним виконанням процедури Sift при зміні параметра L=Ndiv2, ..., 1 :
L:=N div 2 +1;
while L>1 do
Begin
L:=L-1;
Sift(L, N)
end;
Для ілюстації алгоритму розглянемо попередній варіант масиву :
44 |
44 |
44 |
44 | 42
06
Тут жирним шрифтом виділені добавлювані до піраміди елементи; підкреслені - елементи, з якими проводився обмін.
Для того, щоб отримати не тільки часткове, а і повне впорядкування серед елементів послідовності, потрібно виконати N зсувних етапів. Після кожного проходу на вершину дерева виштовхуватиметься черговий найменший ключ. Знову виникає питання : де зберігати "спливаючі" верхні елементи і чи можна проводити перестановки "на тому ж місці"? Це легко реалізувати, якщо кожен раз брати останню компоненту піраміди - це буде просіюваний ключ x, ховати верхній елемент з попереднього етапу в звільнене позицію, а x зсувати на відповідне місце. Зрозуміло, що після кожного етапу розглядувана піраміда буде скорочуватися на один елемент справа. Таким чином, впорядкування масиву буде здійснено за N-1 прохід :
06 42 12 55 94 18 44 67обмін 67 і 06
67 42 12 55 94 18 44 | 06просіювання 67
12 42 18 55 94 67 44 | 06обмін 44 і 12
44 42 18 55 94 67 | 12 06просіювання 44
18 42 44 55 94 67 | 12 06обмін 67 і 18
67 42 44 55 94 | 18 12 06просіювання 67
42 55 44 67 94 | 18 12 06обмін 94 і 42
94 55 44 67 | 42 18 12 06просіювання 94
44 55 94 67 | 42 18 12 06обмін 67 і 44
67 55 94 | 44 42 18 12 06просіювання 67
55 67 94 | 44 42 18 12 06обмін 94 і 55
94 67 | 55 44 42 18 12 06просіювання 94
67 94 | 55 44 42 18 12 06обмін 94 і 67
94 | 67 55 44 42 18 12 06просіювання 94
94 | 67 55 44 42 18 12 06
Тут жирним шрифтом виділені просіювані по піраміді елементи; підкреслені - елементи, між якими проводився обмін.
Процес сортування описується за допомогою процедури Sift таким чином:
R:=N;
while R>1 do
Begin
x:=a[1]; a[1]:=a[R]; a[R]:=x;
R:=R-1;
Sift(1, R)
End;
Як видно з прикладу, отриманий порядок ключів фактично є зворотнім. Це легко виправити, помінявши напрямок відношення порівняння в процедурі Sift на протилежний. Остаточно процедура сортування масиву методом Heap Sort матиме вигляд :
Procedure Heap_Sort;
Var
L, R : integer; x : basetype;
Procedure Sift(L, R : integer);
Var
i, j : integer; x : basetype;
Begin
i:=L; j:=2*L; x:=a[L];
if (j<R) and (a[j]<a[j+1]) then j:=j+1;
while (j<=R) and (x<a[j]) do
Begin
a[i]:=a[j]; a[j]:=x; i:=j; j:=2*j;
if (j<R) and (a[j]<a[j+1]) then j:=j+1
End
End;
Begin
L:=N div 2 +1; R:=N;
while L>1 do
begin L:=L-1; Sift(L, N) end;
while R>1 do
Begin
x:=a[1]; a[1]:=a[R]; a[R]:=x;
R:=R-1;
Sift(1, R)
End
End;
Аналіз алгоритму Heap Sort. Як вже раніше відмічалося, складність алгоритму по операціях порівняння є величиною порядку O(N*log(N)+N). Кількість переміщень елементів суттєво залежить від стартового розміщення ключів в послідовності.
Однак при початково-впорядкованому масиві не слід чекати максимальної ефективності. Адже об’єм перестановок в цьому випадку є досить великим під час просіювання "важких" елементів після побудови піраміди. Фактично на кожному етапі такого просіювання виконується log(K) перестановок плюс ще N-1 обмін перед просіюванням, де K - кількість елементів в піраміді, в якій проводиться просіювання. Таким чином, в цьому випадку
.
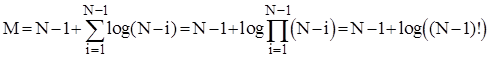Тому можна вважати, що розглядуваний метод як і по порівняннях так і по перестановках має ефективність порядку O(N*log(N)+N).
Висновки
Отже, ми розглянули як працюють швидкі алгоритми сортування іь спробували визначити їх складність.
Застосування того чи іншого алгоритму сортування для вирішення конкретної задачі є досить складною проблемою, вирішення якої потребує не лише досконалого володіння саме цим алгоритмом, але й всебічного розглядання того чи іншого алгоритму, тобто визначення усіх його переваг і недоліків.
Звичайно, необхідність застосування саме швидких алгоритмів сортування очевидна. Адже прості алгоритми сортування не дають бажаної ефективності в роботі програми. Але завжди треба пам’ятати й про те, що кожний швидкий алгоритм сортування поряд із своїми перевагами може містити і деякі недоліки.
Так, алгоритм сортування деревом, хоча й працює однаково на всіх входах (так, що його складність в гіршому випадку співпадає зі складністю в середньому), але цей алгоритм має і досить суттєвий недолік: для нього потрібна додаткова пам’ять розміром 2n-1.
Розглядаючи такий швидкий алгоритм сортування, як пірамідальне сортування, можна зазначити, що цей алгоритм ефективніший ніж попередній, адже він сортує "на місці" , тобто він не потребує додаткових масивів. Крім того, цей алгоритм (" з точністю до мультиплікативної константи" (4,74)) оптимальний: його складність співпадає з нижньою оцінкою задачі, тобто за критеріями C(n) та M(n) він має складність O(n log2 n), але містить складний елемент в умові. Тобто, в умові A[left] має бути строго менше ніж x , а A[right] - строго більше за x. Якщо ж замість "строго більше" та "строго менше" поставити знаки, що позначають "більше, або дорівнює" та "менше, або дорівнює", то індекси left і right пробіжать увесь масив і побіжать далі. Вийти з цієї ситуації можна було б шляхом ускладнення умов продовження перегляду, але це б погіршило ефективність програми.
В нашій роботі ми розглянули деякі швидкі алгоритми сортування та їх реалізацію мовою Pascal, виконуючи курсову роботу ми реалізували програмно не лише використання швидких методів сортування, а і прямих, дослідили не лише переваги таких алгоритмів, ефективність їх використання, але й визначили деякі недоліки окремих алгоритмів, що заважають вживати їх для вирішення першої ліпшої задачі сортування. Програма, в якій міститься реалізація та демонстрація наявних прямих методів сортування називається Prjami. pas, а швидкі - Shvud. pas.
Отже, головною задачею, яку має вирішити людина, яка повинна розв’язати задачу сортування – це визначення як позитивних, так і усіх негативних характеристик різних алгоритмів сортування, передбачення кінцевого результату. До того ж , треба враховувати головне – чи , можливо, цю задачу задовольнить один з класичних простих алгоритмів сортування.
Література
1. Абрамов С. А., Зима Е. В. Начала программирования на языке Pascal. - М.: Наука, 1987.
2. Абрамов В. Г. Введение в язык Pascal: Учебное пособие для студентов вузов по специальности Прикладная математика. – М.: Наука, 1988.
3. Власик А.П. Практикум з програмування в середовищі Turbo Pascal. Ч 1.- Рівне: НУВГП, 2005. – 179 с.
4. Джонс Ж., Харроу К. Решение задач в системе Турбо-Паскаль/ Перевод с английского Улановой, Широкого. – М.: Финансы и статистика, 1991.
5. Зуев Е. А. Язык программирования Турбо Паскаль 6.0, 7.0. – М.: Радио и связь, 1993.
6. Кнут Д.Э. Искуство програмирования, том 3. Поиск и сортировка, 3-е изд.: Пер. с англ.: Уч. Пос. – М.:Издательский дом "Вильямс", 2000. – 750 с.
7. Культин Н. Б. Программирование в TurboPascal 7.0 и Delphi. - Санкт- петербург,1999.
8. Львов М. С., Співаковський О. В. Основи алгоритмізації та програмування. Херсон, 1997.
9. Перминов О. Н. Программирование на языке Паскаль. – М.: Радио и связь, 1988.
10. Перминов О. Н. Язык программирования Pascal. – М.: Радио и свіязь,1989.
11. Турбо Паскаль 7.0 Издание 10-е стереотипное. – Санкт-Петербург: "Печатный Двор", 1999.
12. Фаронов В. В. TurboPascal 7.0 . Начальный курс. – М.: "Нолидж", 2000.
13. Turbo Pascal – Издательская група К.: ВНV, 2000.
Зміст
Вступ
Розділ І. Прямі методи сортування масивів
1.1 Сортування прямим включенням
1.2 Сортування бінарним включенням
1.3 Сортування прямим вибором
1.4 Сортування прямим обміном
Розділ ІІ. Швидкі методи сортування масивів
2.1 Сортування включенням із зменшуваними відстанями – алгоритм Шелла (1959)
2.2 Сортування обміном на великих відстанях – алгоритм Quick Sort
2.3 Сортування вибором при допомозі дерева – алгоритм Тree Sort
2.4 Сортування вибором при допомозі дерева – алгоритм Heap Sort
2.5 Порівняльна характеристика швидкодії деяких швидких алгоритмів сортування
Висновки
Література
Вступ
В наш час нові інформаційні технології посідають дуже важливе місце не лише в спеціалізованих, але й в повсякденних сферах життя. Комп’ютери застосовуються в бізнесі, менеджменті, торгівлі, навчанні та багатьох інших сферах діяльності людини.
Комп’ютерні технології дуже зручні для виконання різноманітних операцій, але в різних сферах застосування ці операції різні. Тому, кожна окрема галузь, яка використовує специфічні технічні засоби, потребує своїх власних програм, які забезпечують роботу комп’ютерів.
Розробкою програмного забезпечення займається така галузь науки, як програмування. Вона набуває все більшого й більшого значення останнім часом, адже з кожним днем комп’ютер стає все більш необхідним, все більш повсякденним явищем нашого життя. Адже обчислювальна техніка минулих років вже майже повністю вичерпала себе і не задовольняє тим потребам, що постають перед людством.
Таким чином, нові інформаційні технології дуже актуальні в наш час і потребують багато уваги для подальшої розробки та вдосконалення. Поряд з цим, велике значення має також і програмування, яке є одним із фундаментальних розділів інформатики і тому не може залишатись осторонь.
Програмування містить цілу низку важливих внутрішніх задач. Однією з найбільш важливих таких задач для програмування є задача сортування. Під сортуванням звичайно розуміють перестановки елементів будь-якої послідовності у визначеному порядку. Ця задача є однією з найважливіших тому, що її метою є полегшення подальшої обробки певних даних і, насамперед, задачі пошуку. Так, одним з ефективних алгоритмів пошуку є бінарний пошук. Він працює швидше ніж, наприклад, лінійний пошук, але його можливо застосовувати лише за умови, що послідовність вже упорядкована, тобто відсортована.
Взагалі, відомо, що в будь-якій сфері діяльності, що використовує комп’ютер для запису, обробки та збереження інформації, усі дані зберігаються в базах даних, які також потребують сортування. Певна впорядкованість для них дуже важлива, адже користувачеві набагато легше працювати з даними, що мають певний порядок. Так, можна розташувати всі товари по назві або відомості про співробітників чи студентів за прізвищем або роком народження, тощо.
Задача сортування в програмуванні не вирішена повністю. Адже, хоча й існує велика кількість алгоритмів сортування, все ж таки метою програмування є не лише розробка алгоритмів сортування елементів, але й розробка саме ефективних алгоритмів сортування. Ми знаємо, що одну й ту саму задачу можна вирішити за допомогою різних алгоритмів і кожен раз зміна алгоритму приводить до нових, більш або менш ефективних розв’язків задачі. Основними вимогами до ефективності алгоритмів сортування є перш за все ефективність за часом та економне використання пам’яті. Згідно цих вимог, прості алгоритми сортування (такі, як сортування вибором і сортування включенням) не є дуже ефективними.
Алгоритм сортування обмінами, хоча і завершує свою роботу (оскільки він використовує лише цикли з параметром і в тілі циклів параметри примусово не змінюються) і не використовує допоміжної пам’яті, але займає багато часу. Навіть, якщо внутрішній цикл не містить жодної перестановки, то дії будуть повторюватись до тих пір, поки не завершиться зовнішній цикл.
Алгоритм сортування вибором ефективніше сортування обмінами за критерієм М(n), тобто за кількістю пересилань, але також є не дуже ефективним. З цих причин було розроблено деякі нові алгоритми сортування, що отримали назву швидких алгоритмів сортування. Це такі алгоритми, як сортування деревом, пірамідальне сортування, швидке сортування Хоара та метод цифрового сортування.
Метою нашої дослідницької роботи є ознайомлення з цими швидкими алгоритмами сортування, спроба проаналізувати їх і висвітлити кожен з них і написати програму, яка б виконувала сортування деякої послідовності за допомогою різних швидких алгоритмів сортування.
Сортування варто розуміти, як процес перегрупування заданої множини об'єктів в деякому конкретному порядку. Мета сортування - полегшити наступний пошук елементів в такій відсортованій множині.
Вибір алгоритму залежить від структури даних, що обробляються. У випадку сортування ця залежність настільки велика, що відповідні методи навіть були розбиті на дві групи - сортування масивів і сортування файлів (послідовностей). Іноді їх називають внутрішнім і зовнішнім і сортуванням, оскільки масиви зберігаються в швидкій внутрішній пам’яті (оперативній) із довільним доступом, а файли розміщуються в менш швидкій, проте більш об'ємній зовнішній пам'яті.
Метод сортування називається стійким, якщо в процесі впорядкування відносне розміщення елементів з рівними значеннями не міняється. Стійкість сортування часто буває бажаною, якщо йде мова про елементи, що вже впорядковані по деяких вторинних ключах (тобто ознаках), які не впливають на основний ключ.
Нехай дано масив N елементів деякого абстрактного типу basetype:
a : array [1..N] of basetype.
Не обмежуючи загальності, зупинимося на впорядкуванні його компонентів по зростанню.
Основна умова: обраний метод сортування масивів повинен економно використовувати доступну пам’ять. Це означає, що перестановки, які приводять елементи в порядок, повинні виконуватися "на тому ж місці". Тобто методи, в яких елементи масиву a передаються в результуючий масив b, не мають практичної цінності.
Алгоритми сортування окрім критерію економії пам’яті будуть класифікуватися по швидкості, тобто по часу їх роботи. Оскільки на різних типах ЕОМ одні і ті ж методи показуватимуть відмінні результати, то в якості міри ефективності алгоритму можуть бути прийняті числа: C - кількість необхідних порівнянь ключів; M - кількість перестановок елементів. Очевидно, що ці числа є функціями від кількості елементів в масиві N. Згідно із введеними критеріями швидкодії алгоритми сортування поділяють на два типи - прямі та швидкі.
Прямі методи зручні для пояснення і розбору основних рис більшості сортувань, легко програмуються і відлагоджуються, а самі програми - короткі, що теж важливо для економії пам’яті. В основі їх лежить повторення N етапів обробки масиву із зменшенням на кожному з них кількості порівнюваних елементів. Ефективність даних алгоритмів є величиною порядку O(N2). Такі методи зручно використовувати на так званих "коротких" масивах.
Швидкі методи вимагають невеликої кількості етапів обробки, однак ці етапи досить складні. На кожному з них окрім переміщення чергового елемента на "своє" місце відбувається перегрупування решти відносно цього елемента. Звичайно виграш по ефективності для таких алгоритмів отримується на "довгих" масивах.
Методи сортування "на тому ж місці" у відповідності із визначаючими їх принципами розбиваються на три основні категорії :
- сортування включенням;
- сортування вибором;
- сортування обміном.
У курсовій роботі ми детально розглянемо швидкі алгоритми сортування елементів масиву, проведемо їх порівняльний аналіз. Крім цього, розглянемо і прямі методи сортування, їх позитиви і недоліки, що дасть змогу краще визначити ефективність і складність швидких алгоритмів сортування.
Розділ І. Прямі методи сортування масивів
Дата: 2019-05-28, просмотров: 298.
