Основна причина повільної роботи алгоритму прямого обміну полягає в тому, що всі порівняння і перестановки елементів в послідовності a 1 , a 2 , ..., a N відбуваються для пар із сусідніх елементів. При такому способі потрібно відносно більше часу, щоб поставити деякий ключ, який знаходиться не на своєму місці, в потрібну позицію у сортованій послідовності. Природньо попробувати пришвидшити цей процес, порівнюючи пари елементів, що знаходяться далеко один від одного в масиві. К. Хоор розробив алгоритм Quick Sort із середнім часом роботи порядку O(N*lnN).
Припустимо, що перший елемент масиву, що сортується, є хорошим наближенням елемента, який вкінці опиниться на своєму місці у відсортованій послідовності. Приймемо його значення в якості ведучого елемента, відносно якого ключі будуть мінятися місцями. Для зручності реалізації алгоритму використаємо два вказівники I, J, перший з яких вестиме відлік вздовж розглядуваної частини масиву зліва, а другий - справа. Початково їх значення будуть відповідно I=1, J=N. Таким чином ведучим елементом буде значення a[I]. Перестановки ключів проводяться за такими принципами :
1) порівнюються елементи a[I] та a[J]; якщо a[I] £a[J], то здійснюється крок вліво J:=J-1 і порівняння повторюється; зменшення J продовжується доти, поки не виконається умова a[I]> a[J];
2) якщо при порівнянні елементів досягнута умова a[I]> a[J], то проводиться обмін місцями кючів a[I] та a[J] і здійснюється крок вправо I:=I+1; таким чином ведучий елемент перейшов в позицію J; порівняння ключів із збільшенням I продовжується доти, поки знову не виконається умова a[I]> a[J];
3) у випадку виконання умови a[I]> a[J] проводиться обмін місцями кючів a[I] та a[J] і здійснюється крок вліво J:=J-1; при цьому ведучий елемент знову повертається в позицію I.
Цей процес із почерговим зменшенням J та збільшенням I повторюється з обох кінців послідовності до "середини"до тих пір, поки не досягнеться I=J.
Тепер мають місце два факти. По-перше, ключ, що був першим у вихідній послідовності, в результаті такого впорядкування опиняється на "своєму" місці. По-друге, всі елементи зліва будуть меншими за нього, а всі ключі справа - більшими.
Ту ж саму процедуру можна використати для впорядкування лівої і правої підпослідовностей і т. д. до повного сортування всьго масиву. Таким чином розглянутий алгоритм має чітко виражений рекурсивний характер. Виходячи з цього, значення індексів крайніх елементів меншої з двох невідсортованих підпослідовностей варто помістити в стекову структуру даних, і приступити до впорядкування більшої підпослідовності.
Оскільки короткі послідовності скоріше сортуються при допомозі прямих методів, то алгоритм Quick Sort матиме вхідний параметр - деяке число S, що визначає нижню межу його використання. Провівши нескладний математичний аналіз нерівності, яка пов’язує ефективності алгоритму Quick Sort та прямих алгоритмів сортування
,
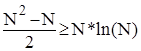можна встановити значення числа S, яке буде нижньою межею використання швидкого сортування. Остання нерівність дає результат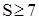 
.
Однак, якщо крім основних операцій порівняння ключів ще враховувати порівняння індексів та перестановки елементів, то це значення можна збільшити в 2-3 рази.
В якості прикладу наводиться програмна реалізація цього алгоритму у вигляд процедури Quick_Sort. В ній використовується два масиви left і right, де зберігатимуться індексні номери відповідно лівої і правої границь підпослідовностей, які ще будуть впорядковуватися на наступних етапах.
Procedure Quick_Sort;
Const S=20;
Var
k, L, R, i, j : integer;
x : basetype;
left, right : array [1..N] of integer;
Begin
k:=1; left[k]:=1; right[k]:=N;
while k>0 do
Begin
L:=left[k]; R:=right[k]; k:=k-1;
while R-L>S do
Begin
i:=L; j:=R; x:=a[i];
while j>i do
Begin
while x<a[j] do j:=j-1;
if j>i then begin
a[i]:=a[j]; a[j]:=x; i:=i+1
end;
while a[i]<x do i:=i+1;
if j>i then begin
a[j]:=a[i]; a[i]:=x; j:=j-1
End
end;
k:=k+1;
if R-i<=i-L then
Begin
left[k]:=i+1; right[k]:=R; R:=i-1
End
Else
Begin
left[k]:=L; right[k]:=i-1; L:=i+1
End
end;
for i:=L+1 to R do
Begin
x:=a[i]; j:=i-1;
while (x<a[j]) and (j>=L) do
Begin
a[j+1]:=a[j]; j:=j-1
end;
a[j+1]:=x
End
End
End ;
Аналіз алгоритму Quick Sort. Щоб оцінити ефективність алгоритму, позначимо через Q(N) середню кількість кроків, необхідних для впорядкування N елементів. Припустимо також, S=1, тобто не використовується сортування прямими методами на коротких послідовностях.
При першому проходженні Quick Sort порівнює всі елементи з ведучим і виконується не більше ніж за C*N кроків, де C - деяка константа. Потім потрібно відсортувати дві підпослідовності довжинами I-1 та N-I. Тому середня кількість кроків, потрібних для впорядкування N елементів, залежить від середньої кількості кроків, потрібних для впорядкування I-1 та N-I елементів відповідно. Оскільки всі можливі значення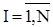 
є рівноймовірними, то спрведлива наступна оцінка :
.
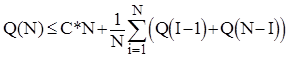Врахувавши, що
,
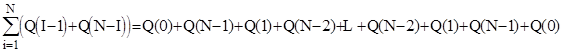отримаємо
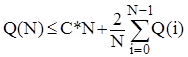.(1)
Покажемо за індукцією по N, що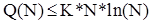 
для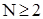 
, де K=2C+2B, B=Q(0)=Q(1). Останнє співвіднощення означає, що Quick Sort вимагає постійної однакової кількості кроків для впорядкування 0 або 1 елемента.
1) N=2 :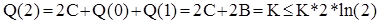 
;
2) припустимо, що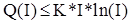 
для I=2, 3, ..., N-1 ;
3) перевіримо справедливість для I=N. Співвідношення (1) з врахуванням попереднього припущення можна переписати у вигляді
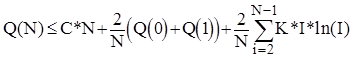або
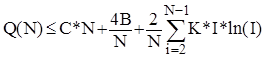.(2)
Оскільки функція I*ln(I) є опуклою вниз, то для цілих значень аргументу справедлива оцінка
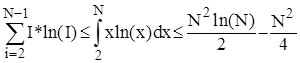
Врахувавши останню нерівність, із співвідношення (2) одержимо
.
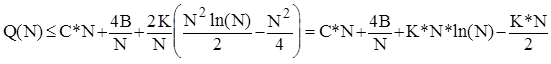Оскільки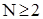 
, то
.
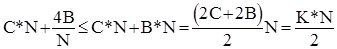Остаточно отримаємо
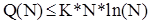.(3)
Таким чином ефективність алгоритму Quick Sort є величина порядку O(N*ln(N)).
Всі наведені викладки справедливі для аналізу по операціях порівняння. Кількість же перестановок залежить від початкового розміщення елементів у послідовності. Характерно, що для цього методу у випадку зворотньо впорядкованого масиву об’єм переміщень ключів не буде максимальним. Адже на кожному етапі ведучий елемент буде найбільшим і опиниться на своєму місці після першого ж порівняння і перестановки, тобто M=N-1. Максимальна кількість переприсвоєнь ключів співпадатиме з кількістю порівнянь, мінімальна - рівна нулю.
Алгоритм Quick Sort, як і розглянуті прямі методи, описує процес стійкого сортування.
Дата: 2019-05-28, просмотров: 200.
