Сортування включенням із зменшуваними відстанями – алгоритм Шелла (1959)
Шелл вдосконалив пряме включення. Він запропонував проводити послідовне впорядкування підмасивів з елементів, які знаходяться на великих відстанях. При цьому на кожному наступному етапі відстані між елементами в групах мають зменшуватися.
Для ілюстрації алгоритму розглянемо його покрокове описання. Не обмежуючи загальності, в якості прикладу спочатку зупинимося на масиві з кількістю елементів, що є степенем двійки, тобто 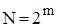 :
:
1) на першому етапі окремо групуються і сортуються елементи, розміщені на відстані N/2 . Це є впорядкування N/2 підмасиві по 2 елементи, яке називатимемо N/2-сортування .
2) на другому етапі виконується впорядку вання N/4 підмасивів по 4 елементи на відстані N/4 - N/4-сортування і т.д.
На останньому етапі виконується одинарне сортування (впорядкування на відстані 1). Наприклад :
44 55 12 42 94 18 06 67
етап I-сортування
44 18 06 42 94 55 12 67
етап II-сортування
06 18 12 42 44 55 94 67
етап III-сортування
06 12 18 42 44 55 67 94
Виникає питання, чи використання багатьох процесів сортування із залученням всіх елементів не збільшить кількість операцій, тобто складність алгоритму? Але на кожному проході або впорядковується відносно мало елементів (початкові етапи), або елементи вже досить добре впорядковані і вимагається відносно мало перестановок (кінцеві етапи). Кожне i-те сортування об’єднує дві групи, вже впорядковані 2i-тим сортуванням. Очевидно, що відстань між елементами груп можна зменшувати по-різному, головне, щоб остання була одиничною. Останній прохід в найгіршому випадку і виконує основну роботу. Варто зауважити, що такий довільний підхід при зменшенні відстаней не погіршує результату і у випадку кількості елементів N, що не є степенем двійки.
Нехай виконується t етапів. Відстані між елементами в окремих групах на кожному етапі позначимо : h1 , h2 , ..., h t , де h t=1, h i+1<h i , i=1, 2, ..., t-1. Таким чином розглядаються h-ті сортування. Кожне h-те сортування можна реалізувати будь-яким із прямих методів. Зокрема, вибір включення оправданий кращою в порівнянні з іншими алгоритмами ефективністю по перестановках ключів. Однак, чи варто для спрощення умови припинення пошуку місця включення чергового елемента користуватися методом бар’єрів? Оскільки кожне h-те сортування потребує свого власного бар’єра, то прийдеться розширити масив не на одну компоненту a0 , а на h1 компонент. На першому етапі - це практично половина всіх елементів. У випадку "довгих" масивів прийдеться порушити правило сортування "на своєму місці". Тому не варто заради економії однієї логічної операції на кожному етапі впорядкування жертвувати такими об’ємами пам’яті.
Кількість етапів сортування t як і відстані на кожному з них можна вибирати довільно. Зокрема, це може бути кількість цілочисельних поділів числа N на 2, тобто t=[log(N)]. В якості прикладу пропонується процедура сортування методом Шелла для масиву із 16 елементів :
Procedure Shell_Sort;
Const t=4;
Var
m, i, j, k : integer;
h : array [1..t] of integer;
x : basetype;
Begin
h[1]:=8; h[2]:=4; h[3]:=2; h[4]:=1;
for m:=1 to t do
Begin
k:=h[m];
for i:=k+1 to N do
Begin
x:=a[i]; j:=i-k;
while (x<a[j]) and (j>0) do
Begin
a[j+k]:=a[j]; j:=j-k
end;
a[j+k]:=x
End
End
End;
Аналіз алгоритму Шелла . Поки що не має чітко обгрунтованих виборів відстаней, які давали б найкращу ефективність. Самим цікавим є те, що ці відстані не повинні бути множниками один одного, а тим більше степенями деяких чисел. Це дозволяє уникнути явища, коли на певному етапі взаємодіють дві групи, які до цього ніде ще не перетиналися. Взагалі, бажано, щоб взаємодія окремих ланцюгів відбувалася якомога частіше. Вірною є наступна теорема :
Теорема. Якщо k-відсортовану послідовність i-відсортувати, то вона при цьому залишиться k-відсортованою.
Кнут рекомендує використовувати такі послідовності відстаней, записані в зворотньому порядку :
1, 4, 13, 40, 121, ... , де h i-1=3 h i+1 , h t=1 , t=[ log 3 N]-1 , або
1, 3, 7, 15, 31, ... , де h i-1=2 h i+1 , h t=1 , t=[ log 2 N]-1.
З обчислювальної практики відомо, що загалом метод Шелла має ефективність порядку O(N1,2).
Дата: 2019-05-28, просмотров: 298.