Быстродействие САР оценивают по времени окончания переходного процесса (t_п). Время переходного процесса  t_п определяется как время, через которое регулируемая величина «входит в коридор» шириной 2Δ вокруг установившегося значения  y_∞ . Это значит, что при t _п > t значение выхода отличается от установившегося не более, чем на Δ. Обычно величина Δ задается в процентах от установившегося значения, чаще всего 2% или 5%. Заметим, что для апериодического звена с постоянной времени τ время переходного процесса равно t_п = 3τ (с точностью 5%).

Запас устойчивости оценивают по перерегулированию – σ, значение которой показывает на сколько процентов максимальное значение выхода y_max превышает установившееся значение  y_∞ :

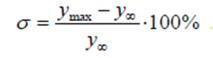
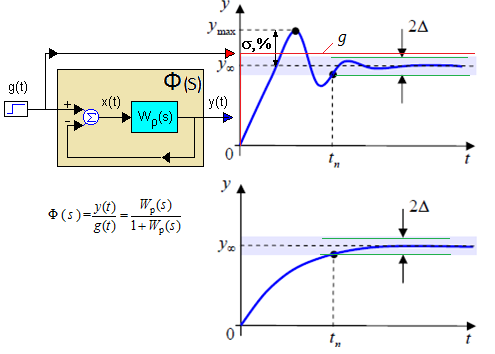
Рис.4

Нулевое перерегулирование удается обеспечить при апериодическом переходном процессе. Необходимо помнить, что увеличение быстродействия обычно приводит к увеличению перерегулирования.

Частотные оценки качества

Качество системы можно оценить не только по переходной характеристике, но по частотной характеристике.

Критерий Найквиста позволяет определить устойчивость замкнутой системы, построив частотную характеристику разомкнутой системы. Пусть W_p(s) – передаточная функция разомкнутой системы, а W_p(ω j) – ее частотная характеристика. Соответственно можно выделить амплитудночастотную A(ω) и фазочастотную φ(ω) характеристики. 

Частота ω_cр, для которой A(ω_cр)=1, называется частотой среза. Для устойчивой системы значение фазы на частоте среза должно быть больше, чем −180°.

Вместо A(ω) обычно используют логарифмическую амплитудную частотных характеристику (ЛАЧХ): график, на котором по оси абсцисс откладывается десятичный логарифм частоты lg(ω), а по оси ординат – величина L_m(ω) = 20lgA(ω), измеряемая в децибелах (дБ). При построении логарифмической фазовой частотной характеристики (ЛФЧХ) по оси абсцисс также откладывается логарифм частоты lg ω. 

Недостаточно спроектировать просто устойчивую систему, нужно, чтобы система, обладала некоторым запасом устойчивости. Чем выше запас устойчивости, тем лучше качество системы.

Обычно рассматривают запасы устойчивости по амплитуде и по фазе. Запас устойчивости по амплитуде g_m – это дополнительное усиление контура, которое необходимо, чтобы вывести систему на границу области устойчивости. Эта величина измеряется в децибелах.

Запас по амплитуде вычисляется по формуле g_m = 20lg( 1/ A_g),

где A_g < 1 значение амплитудной характеристики на частоте ω_g, где фазовая характеристика равна −180°.

Запасы устойчивости легко определяются по логарифмическим частотным характеристикам:

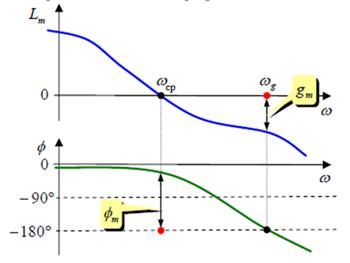
Рис. 5

Заметим, что запас по амплитуде может быть равен бесконечности, если фазовая характеристика не пересекает линию −180° .

Частота среза 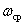 косвенно характеризует длительность переходного процесса. Время регулирования системы обратно пропорционально частоте среза. Частота среза, как характеристика быстродействия систем получила распространение, так как она легко определяется на логарифмических частотных характеристиках.

Корневая оценка качества

Поскольку корни передаточной функции Φ(s)= 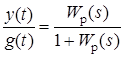, однозначно определяют вид переходного процесса, их можно использовать для оценки устойчивости и быстродействия. Обычно обходятся исследованием только полюсов Φ(s), т.е. корней характеристического уравнения (полинома) D(s)=1+W(s)=0. Свойства системы можно предсказать, посмотрев на расположение корней характеристического полинома на комплексной плоскости. Прежде всего, все корни D(s) для устойчивой системы должны находиться в левой полуплоскости, то есть слева от мнимой оси.

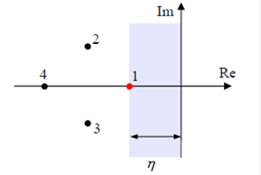
Рис.6

Быстродействие системы определяется степенью быстродействия η – так называется расстояние мнимой оси до ближайшего корня или пары комплексно-сопряженных корней. Т.е. если этот корень −α±jβ, то η равна коэффициенту затухания α.

На рисунке точками отмечены положения корней характеристического полинома. Он имеет два вещественных корня (обозначенных номерами 1 и 4) и пару комплексно сопряженных корней (2 и 3). Степень быстродействия определяется корнем наиболее ближе всех расположенным к мнимой оси (корень 1 в нашем случае). Этот корень называется доминирующим, он определяет самые медленные движения в системе и время переходного процесса, которое может быть примерно рассчитано по формуле

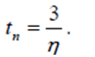
Корни 2, 3 и 4 соответствуют более быстрым движениям.

Параметр, определяющий скорость затухания колебаний в системе, называется колебательностью. Колебательность μ для пары комплексно-сопряженных корней α ± jβ вычисляется как отношение мнимой и вещественной частей корня (по модулю):

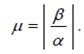
Чем больше эта величина, тем слабее затухают колебания, вызванные этими корнями, за 1 период колебаний.

Линии постоянной колебательности – это лучи, выходящие из начала координат. При проектировании систем обычно требуется обеспечить быстродействие не ниже заданного (степень быстродействия не меньше заданной η_min) и колебательность не выше заданной μ_max. Эти условия определяют усеченный сектор на комплексной плоскости.

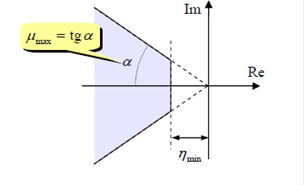
Рис.3.7

Колебательность определяет другой показатель ξ – относительный коэффициент затухания амплитуды колебаний y(t)=Ce^−αtsin(βt+φ) за один период:

.

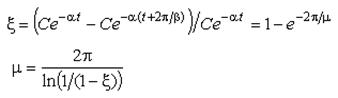Чем больше ξ, тем быстрее затухают колебания. При ξ≥1 процессы носят апериодический характер.

Условия устойчивости